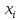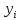Текст. 7. Пример выполнения контрольной работы
 Скачать 40.44 Kb. Скачать 40.44 Kb.
|
|
7. Пример выполнения контрольной работы Функция y(x) задана таблично:
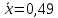 Задание 1. Вычислить значение функции y(x) в точке 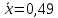 , используя линейную интерполяцию. , используя линейную интерполяцию.Линейная интерполяция заключается в том, что функция y(x) заменяется ломаной с вершинами в точках ( 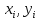 ). Так как ). Так как 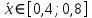 , находим уравнение прямой, проходящей через две точки (0,4; 4,1) и (0,8; 4,2): , находим уравнение прямой, проходящей через две точки (0,4; 4,1) и (0,8; 4,2):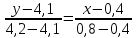 Отсюда 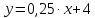 . .При 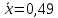 имеем y( имеем y(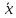 )≈4,1225. )≈4,1225.Задание 2. Вычислить значение функции y(x) в точке 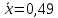 , используя квадратичную интерполяцию (интерполяционный многочлен Лагранжа второй степени). , используя квадратичную интерполяцию (интерполяционный многочлен Лагранжа второй степени).При квадратичной интерполяции таблично заданная функция заменяется совокупностью дуг, имеющих форму парабол, каждая из которых проходит через три соседние точки. Уравнение параболы, проходящей через точки 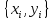 ( (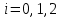 ), задает многочлен Лагранжа второй степени: ), задает многочлен Лагранжа второй степени: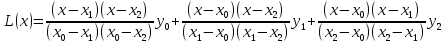 Из условия задачи видно, что тремя ближайшими к 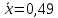 точками являются: (0,4; 4,1), (0,8; 4,2) и (1,2; 6,2). Подставив их координаты в L(x) и приняв точками являются: (0,4; 4,1), (0,8; 4,2) и (1,2; 6,2). Подставив их координаты в L(x) и приняв 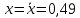 , найдем: , найдем: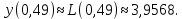 Итак, используя линейную интерполяцию, мы получили 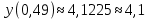 , тогда как при квадратичной функции y(x) в точке , тогда как при квадратичной функции y(x) в точке 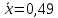 , найденные двумя разными способами, отличаются друг от друга приблизительно на 3%. , найденные двумя разными способами, отличаются друг от друга приблизительно на 3%.Какое из двух найденных значений точнее, сказать трудно без дополнительной информации об исходной функции y(x), следовательно, нельзя определить, какой вид интерполяции предпочтительнее. В то же время, можно отметить, что квадратичная интерполяция представляет поведение функции y(x) на более широком интервале [0,4; 1,2] по сравнению с линейной, когда 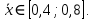 В этом смысле квадратичная интерполяция может оказаться более предпочтительной. В этом смысле квадратичная интерполяция может оказаться более предпочтительной.Задание 3. Для заданной функции y(x) построить аппроксимирующей многочлен третьей степени 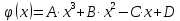 на отрезке [ на отрезке [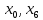 ] методом наименьших квадратов. При этом определение коэффициентов A, B, C, D из системы линейных алгебраических уравнений выполнить методов Гаусса. Найти значение функции ] методом наименьших квадратов. При этом определение коэффициентов A, B, C, D из системы линейных алгебраических уравнений выполнить методов Гаусса. Найти значение функции 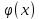 в заданной точке в заданной точке 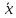 . .В качестве одного из способов аппроксимации функции рассмотрим метод наименьших квадратов, в котором мерой отклонения многочлена 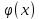 от таблично заданной функции y(x) является величина: от таблично заданной функции y(x) является величина: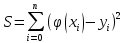 Где n – количество узлов аппроксимации (n=6 в нашем примере);  имеют смысл неких констант, заданных по условию задачи; имеют смысл неких констант, заданных по условию задачи; 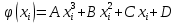 , следовательно, определенно в S подлежат неизвестные коэффициенты A, B, C, D. Метод наименьших квадратов предполагает вычисление A, B, C, D из условия минимума среднеквадратичного отклонения S, которое в нашем случае полиноминальной аппроксимирующей функции имеет вид системы линейных алгебраических уравнений: , следовательно, определенно в S подлежат неизвестные коэффициенты A, B, C, D. Метод наименьших квадратов предполагает вычисление A, B, C, D из условия минимума среднеквадратичного отклонения S, которое в нашем случае полиноминальной аппроксимирующей функции имеет вид системы линейных алгебраических уравнений: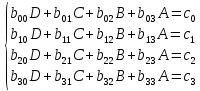 Где 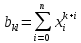 , , 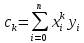 (k, l=0, 1, 2, 3) – константы. (k, l=0, 1, 2, 3) – константы.В нашем примере n=6, и для вычисления этих констант удобно подготовить таблицу вида:
Подставляя в формулы соответствующие значения из последней строки, получаем: 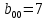 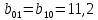 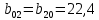 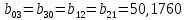 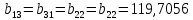 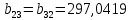 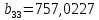 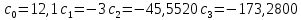 Тогда система уравнений для определения неизвестных A, B, C, D пример следующий вид: 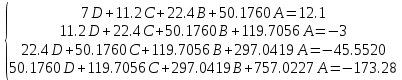 Решение системы проводим методом Гаусса. Матрица коэффициентов при неизвестных 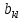 ( (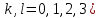 и свободных членов и свободных членов 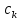 имеет вид: имеет вид: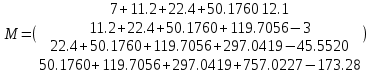 Прямой ход. Приводим матрицу M к треугольному виду. Матрица M принимает вид. 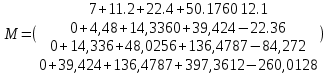 Аналогичной процедурой получаем нули во втором и третьем столбцах: 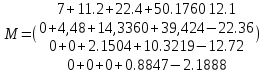 Наконец делим каждую строку на соответствующий ей диагональный элемент. В результате матрица коэффициентов системы примет вид: 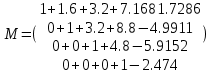 Обратный ход По полученной матрице  составляем систему линейных уравнений. составляем систему линейных уравнений.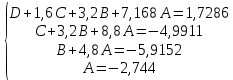 Начиная с последнего уравнения, находим все неизвестные подстановкой их значений из нижестоящих в вышестоящие уравнения. Итак, коэффициенты аппроксимирующего многочлена найдены: 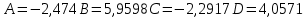 Следовательно, 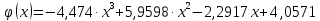 И значение функции y(x) в точке 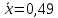 составляет: составляет: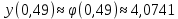 Задание 4. Вычислить величину определенного интеграла для таблично заданной функции 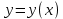 методом трапеций. Сравнить полученное значение с величиной, найденной по формуле Ньютона-Лейбница: методом трапеций. Сравнить полученное значение с величиной, найденной по формуле Ньютона-Лейбница: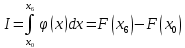 где 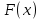 – первообразная функция для кубического аппроксимирующего y(x) полинома φ(x). – первообразная функция для кубического аппроксимирующего y(x) полинома φ(x).В нашем примере i=0, 1,…, 6 причем, все 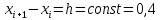 , то есть имеем равноотстоящие узлы. Тогда: , то есть имеем равноотстоящие узлы. Тогда: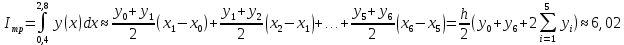 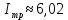 - величина определенного интеграла, найденная по методу трапеций, то есть с применение для подынтегральной функции линейной интерполяции. - величина определенного интеграла, найденная по методу трапеций, то есть с применение для подынтегральной функции линейной интерполяции.С другой стороны, в задании 3 мы описали исходную таблично заданную функцию с помощью аппроксимирующего полинома 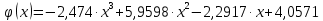 Такое представление подынтегральной функции допускает вычисление определенного интеграла первообразную для φ(x), равную 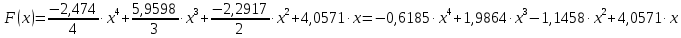 Тогда по формуле Ньютона-Лейбница имеем: 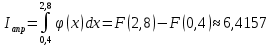 Разница между результатами двух подходов к вычислению определенного интеграла составляет менее 7%. Увеличение точности интегрирования может быть достигнуто, например, уменьшением шага h=0,2, то есть уменьшили исходных шаг вдвое, тогда получили 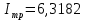 , что значительно ближе к , что значительно ближе к 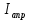 . .Задание 5. Найти наибольшее ( 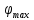 ) и наименьшее ( ) и наименьшее (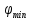 ) значения для непрерывной на отрезке [ ) значения для непрерывной на отрезке [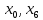 ] унимодальной функции φ(x). Определить точки ] унимодальной функции φ(x). Определить точки 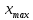 и и 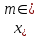 , в которых эти значения достигаются. Задачу решить двумя способами: , в которых эти значения достигаются. Задачу решить двумя способами:А) Методом дифференциального исчисления; Б) Численным методом золотого сечения. Сравнить результаты двух подходов. Функция 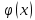 непрерывна на отрезке [ непрерывна на отрезке [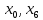 ], следовательно, по теореме Вейерштрасса она достигает своих экстремальных значений либо на концах отрезка, либо в одной из критических точек, определяемых из условия ], следовательно, по теореме Вейерштрасса она достигает своих экстремальных значений либо на концах отрезка, либо в одной из критических точек, определяемых из условия 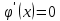 . В нашем случае . В нашем случае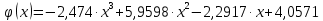 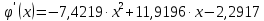 Тогда критические точки найдем из уравнения 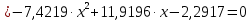 Это квадратное уравнение и его корни легко вычисляются: 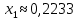 и и 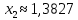 . .Точка 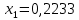 не входит в исследуемый отрезок [ не входит в исследуемый отрезок [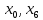 ]=[0,4, 2,8], следовательно, в пределах рассматриваемой области имеем единственную критическую точку ]=[0,4, 2,8], следовательно, в пределах рассматриваемой области имеем единственную критическую точку 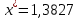 , тогда , тогда 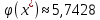 . .Вычислим функцию φ(x) в граничных точках: 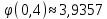 , , 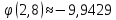 . .Сравнив найденные значения φ(0,4), φ(1,3827) и φ(2,8) заключаем: 1) Наибольшее значение функции φ(х) на отрезке [ 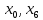 ] достигается в точке ] достигается в точке 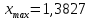 и составляет и составляет 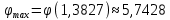 ; ;2) Наименьшее значение функции 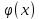 на отрезке [ на отрезке [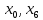 ] достигается в точке ] достигается в точке 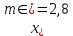 и составляет и составляет 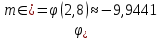 . .Способ b) Рассмотрим другой подход к решению задачи о локальных экстремумах, так называемые методы поиска, в частности, метод золотого сечения. Его применимость в нашем случае очевидна, так как по условию задачи функция φ(x) является унимодальной. Шаг 1. Полагаем 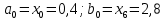 . Выбираем две внутренние для этого интервала [ . Выбираем две внутренние для этого интервала [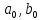 ] точки, координаты которых вычисляются из условия золотого сечения: ] точки, координаты которых вычисляются из условия золотого сечения: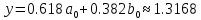 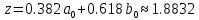 Вычисляем φ(y) и φ(z) (результаты всех вычислений заносим в таблицу, приведенную ниже). Поскольку 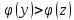 , то , то 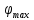 находится на отрезке [ находится на отрезке [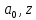 ] и [ ] и [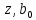 ] можно исключить из дальнейшего рассмотрения. ] можно исключить из дальнейшего рассмотрения.Шаг 2. Полагаем 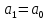 ; ; 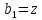 ; ; 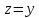 . Новое значение y вычисляем по формуле: . Новое значение y вычисляем по формуле: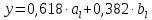 Находим φ(y) и φ(z), поскольку 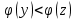 , то , то 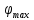 находится на отрезке [z, находится на отрезке [z, 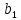 ]. ].Шаг 3. Полагаем 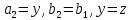 . Вычисляем новое z; . Вычисляем новое z;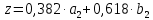 Находим φ(y) и φ(z), сравниваем между собой и уменьшаем интервал по результатам сравнения. Процесс продолжается до тех пор, пока 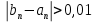 . При выполнении условия . При выполнении условия 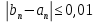 , полагаем , полагаем 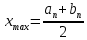
В нашем примере решение достигается на 12-м шаге (при 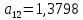 , , 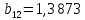 ): ):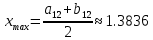 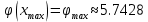 Сравнив полученные 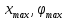 с результатами первого подхода, обнаруживаем хорошее соответствие между ними, что свидетельствует о правильности найденного решения. с результатами первого подхода, обнаруживаем хорошее соответствие между ними, что свидетельствует о правильности найденного решения.Задание 6. Найти один из нулей функции 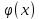 (корень уравнения (корень уравнения 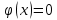 ) методом бисекции с точностью ) методом бисекции с точностью 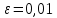 . .Численное решение нелинейных уравнений проходит в два этапа: 1) Отделение корня (построение интервала изоляции корня); 2) Уточнение корня до заданной наперед величины 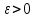 . .Рассмотрим выполнение первого этапа. Находим отрезок [a, b], содержащей единственный корень уравнения 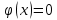 . Для непрерывной и монотонной на [a, b] функции . Для непрерывной и монотонной на [a, b] функции 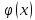 необходимое и достаточное условие единственности корня уравнения необходимое и достаточное условие единственности корня уравнения 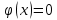 в пределах [a, b] следующее: в пределах [a, b] следующее: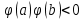 Т.е. функция меняет знак на концах отрезка. Для нашего примера, используя результаты задания 5, можно заключить, что всем перечисленным условиям удовлетворяет интервал [a, b]=[2, 2.8]. Переходим ко второму этапу. Процедура метода бисекции [1,3,4] принципиально аналогична рассмотренной нами в задании 5 (способ b); строится последовательность отрезков [  ], [ ], [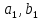 ], …, [ ], …, [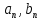 ], стягивающихся к нулю функции φ(x). Отличия в следующем: ], стягивающихся к нулю функции φ(x). Отличия в следующем:a) исходный на каждом шаге отрезок делится пополам; б) следующий отрезок из двух, равных половинам предыдущего, выбирается из условия: произведение значений функции φ(x) на концах первого отрезка – отрицательно; с) Решение считается найденным, если 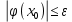 , где , где 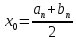 , либо если , либо если 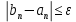 , тогда точка , тогда точка 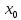 считается нулем функции φ(x). считается нулем функции φ(x).Продемонстрирует процедуру на нашем примере. Шаг 1. Полагаем a=2; b=2,8. Находим точку 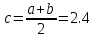 . Вычисляем . Вычисляем 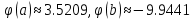 . Поскольку . Поскольку 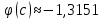 , то нуль функции φ(x) лежит на отрезке [a, c], а другую половину – (c, b] можно исключить из дальнейшего рассмотрения. Процесс продолжаем, так как , то нуль функции φ(x) лежит на отрезке [a, c], а другую половину – (c, b] можно исключить из дальнейшего рассмотрения. Процесс продолжаем, так как 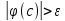 и и 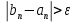 . Результаты всех вычислений заносим в таблицу, приведенную ниже. . Результаты всех вычислений заносим в таблицу, приведенную ниже.Шаг 2. Полагаем a=2; b=2.4. Находим середину (точку с) полученного отрезка [a, b] и вычисляем в ней значение функции φ(х). Так как это значение больше точности ε, то сравниваем его со значениями функции на концах отрезка [a, b] и исключаем из дальнейшего рассмотрения ту половину, на которой функция φ(x) не меняет знак. Поскольку длина половины отрезка [a, b] больше точности ε, переходим к следующему шагу. И так далее, пока не выполнится одно из вышеприведенных условий прекращения процесса. Таблица результатов вычислений имеет вид:
В нашем примере решение достигается на 8-м шаге. Из приведенной таблицы результатов вычислений видно что, по второму критерию 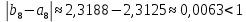 (хотя по первому критерию 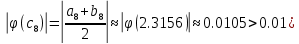 . .Следовательно, 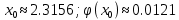 |