8. Определение среднего времени исправной работы
 Скачать 36.92 Kb.
|
|
8. Определение среднего времени исправной работы Средним временем безотказной работы называется математическое ожидание времени безотказной работы. Эта характеристика надежности обозначается T. Как всякое математическое ожидание случайной величины среднее время безотказной работы определяется из выражения:  . (1)Приведенное определение является вероятностным. Для определения среднего времени безотказной работы из статистических данных пользуются формулой: 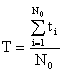 , (2)где ti- время безотказной работы i-го образца, N0- число образцов, над которыми проводится испытание. Из выражения (2) видно, что для определения T необходимо знать моменты отказов всех образцов аппаратуры, над которыми проводится эксперимент. При большом числе образцов N0 это может сильно усложнить эксперимент. Выражение (2) является статистическим определением среднего времени безотказной работы. Среднее время безотказной работы является одной из наиболее наглядных количественных характеристик надежности. Однако этой характеристике надежности свойственны существенные недостатки. Как математическое ожидание случайной величины, она не может полностью характеризовать время работы аппаратуры. Необходимо еще знать, по меньшей мере, дисперсию времени отказов аппаратуры. Кроме того, T фактически не позволяет оценить надежность аппаратуры, время работы которой во много раз меньше среднего времени безотказной работы. Из выражения (26 видно, что для вычисления T определяются времена отказов каждого из N0 образцов. В дальнейшем они в эксперименте не участвуют. Таким образом, среднее время безотказной работы характеризует надежность аппаратуры до первого отказа. Это означает, что T хорошо характеризует надежность аппаратуры разового использования, например, простейших элементов, которые после отказа не ремонтируются. Величину T можно использовать и для оценки надежности сложных устройств. Однако в этом случае T характеризует надежность до первого их отказа. У аппаратуры длительного использования, работающей в режиме смены отказавших элементов, среднее время безотказной работы до первого отказа может существенно отличаться от среднего времени между первым и вторым отказами, вторым и третьим и т.д. Это означает, что среднее время безотказной работы может характеризовать надежность такой аппаратуры только до первого отказа. Поэтому надежность аппаратуры длительного использования оценивают, в отличие от среднего времени безотказной работы, так называемой наработкой на отказ. Этой характеристике дают следующее определение: наработкой на отказ называется среднее значение времени между соседними отказами, при условии восстановления каждого отказавшего элемента. Эта характеристика обозначается tср и определяется из статистических данных об отказах по формуле:  , (3)где ti – время исправной работы аппаратуры между (i – 1)-м и i-м отказами; n – число отказов аппаратуры за время t. Из определения и формулы (3) видно, что наработка на отказ является средним временем между соседними отказами. Если испытание проводится с несколькими образцами, то tср вычисляется по формуле: 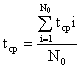 (4)где tср.i - среднее время между соседними отказами i-го образца, вычисленное по формуле (4), N0 – число испытываемых образцов. Найти связь среднего времени между соседними отказами с другими количественными характеристиками надежности проще всего через среднюю частоту отказов. Действительно, если известны средние частоты отказов элементов сложной системы, то среднее число отказов системы в любом промежутке времени определяется ее суммарной частотой отказов. Тогда среднее время между соседними отказами будет равно величие, обратной суммарной частоте отказов, т.е.  (5)или  , (6)где r – число типов элементов. Вероятность безотказной работы P(t), частота отказов α(t) (средняя частота отказов  ), интенсивность отказов  и среднее время безотказной работы T (среднее время между соседними отказами tср) являются основными количественными характеристиками надежности. Вероятность безотказной работы первичных преобразователей в течение t = 1000 час равна Р (1000) = 0,95. Для повышения надежности системы автоматизации имеется такой же преобразователь, который включается в работу при отказе первого (имеет место холодный резерв). Требуется определить вероятность безотказной работы и среднюю наработку до первого отказа системы, состоящей из двух преобразователей. Решение. Из условия задачи видно, что имеет место общее резервирование замещением кратности m = 1. Тогда 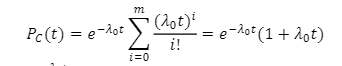 Из условий задачи  = 0,95, тогда  = 0,05.Подставляем значение Р(1000) и полученное значение в выражение  получим = 0,95(1+0,05)=0,9975Средняя наработка до первого отказа системы будет  Так как в течение времени t = 1000 час  =0,05, то  = 0,05/t ==0,05/1000=0,5*10-4 ч-1, а средняя наработка до первого отказа нерезервированного преобразователя  = 1/ 0,5*10-4 = 20 000 час.Тогда средняя наработка до первого отказа резервированной системы будет  = 2*20 000 = 40 000 час.Варианты для расчета:
|