УвОС. РАЗДЕЛ 9. 9 Область применения и сущность экспертных методов

• Название: 9 Область применения и сущность экспертных методов
• Дата: 22.11.2020
• Размер: 81.99 Kb.
• Имя файла: РАЗДЕЛ 9.docx
• Тип: Задача; #152738
• страница: 1 из 2

РАЗДЕЛ 9. ПРИМЕНЕНИЕ МЕХАНИЗМОВ ЭКСПЕРТИЗЫ В ЗАДАЧАХ УПРАВЛЕНИЯ
Область применения и сущность экспертных методов. Методы получения экспертных оценок. . Обработка и анализ экспертных оценок. Метод анализа иерархий
9.1. Область применения и сущность экспертных методов
Экспертные оценки используются для анализа и последующего прогнозирования:

1. 
   для объектов, развитие которых не поддается предметному описанию и математической формализации;
   
2. 
   в условиях отсутствия достоверной информации о характеристиках объекта;
   
3. 
   в условиях большой неопределенности среды функционирования объекта (рыночной среды);
   
4. 
   при отсутствии необходимых технических и финансовых возможностей;
   
5. 
   в экстремальных ситуациях.
   

Идея применения экспертных методов заключается в получении новой информации из исходной с привлечением компетентных в данной области людей, которые проводят интуитивно-логический анализ с целью вынесения суждения и рекомендаций по нему. Суждения экспертов обрабатываются при помощи определенных математических процедур. В результате получаются экспертные оценки, которые не являются решением, а лишь помогают ЛПР в принятии решения.
Область применения метода экспертных оценок весьма широка. Перечислим типовые задачи, решаемые методом экспертных оценок:

1) составление перечня возможных событий в различных областях за определенный промежуток времени;

2) определение наиболее вероятных интервалов времени свершения совокупности событий;

3) определение целей и задач управления с упорядочением их по степени важности;

4) определение альтернативных (вариантов решения задачи с оценкой их предпочтения;

5) альтернативное распределение ресурсов для решения задач с оценкой их предпочтительности;

6) альтернативные варианты принятия решений в определенной ситуации с оценкой их предпочтительности.
Этапы экспертизы:

1. 
   формирование цели и задач
   
2. 
   выбор метода экспертного оценивания (метод интервью, метод анкетирования, метод сценариев, метод Делфи и др.)
   
3. 
   подбор экспертной группы
   
4. 
   экспертиза
   
5. 
   обработка и анализ результатов
   
6. 
   интерпретация полученных результатов
   
7. 
   составление отчета.
   

Методы организации экспертного оценивания подробно описаны в различных литературных источниках поэтому подробно останавливаться на них в рамках данного пособия мы не будем. С нашей точки зрения, при построении систем поддержки принятия решений необходимо особое внимание уделить процедурам обработки результатов экспертизы, так как этот этап может быть формализован и автоматизирован.
9.2. Методы получения экспертных оценок
Рациональное использование информации, полученной от экспертов, возможно при условии преобразования ее в форму, удобную для дальнейшего анализа при принятии решений.

Для того, чтобы формализовать оценки, полученные от экспертов и представить их в цифровой форме можно использовать следующие методы.

А) ранжирование.

Рассмотрим данный метод на следующем примере:
Пример.9.1. Эксперты оценили ценность объектов d1, d2,d3,d4,d5,d6 следующим образом: d1>d3d4>d6>d2d5. Определить ранг каждого из объектов
Решение:

Необходимо приписать каждому из объектов числовой вес в зависимости от их порядка расположения (чем выше оценен объект, тем меньше ранг). Если объекты оценены одинаково, им присваивается ранг, определяемый как среднее арифметическое из порядковых номеров этих объектов.

D1	D3	D4	D6	D2	D5
1	2	3	4	5	6
1	2,5	2,5	4	5,5	5,5

Такое ранжирование называется нестрогим, так как несколько элементов могут иметь одинаковые численные оценки. Строгое ранжирование выполняется в тех случаях, когда можно указать различные числовые оценки для каждого оцениваемого фактора.
Недостаток этого метода состоит в том, что предельное количество элементов, когда можно использовать ранжирование – 20.
б) балльные оценки

Сущность балльных оценок состоит в том, что каждый эксперт должен приписать объекту или фактору определенный балл по некоторой шкале.
Пример 9.2. Пусть в результате опроса n=3 экспертов были получены следующие балльные оценки при оценке m=4 факторов:

	1 эксперт	2 эксперт	3 эксперт
1 фактор	10	8	7
2 фактор	8	9	6
3 фактор	10	10	7
4 фактор	9	9	7

Определить групповую оценку по каждому фактору.
Решение

В качестве групповых оценок принимают средние балльные оценки для каждого фактора:

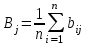(9.1)
Получим групповые оценки:

1 фактор: 8,3 балла

2 фактор: 7,6 баллов

3 фактор: 9 баллов

4 фактор: 8,3 балла
в) точечные оценки.

Если при проведении экспертизы каждый эксперт должен оценить непосредственную числовую характеристику некоторого объекта (вероятность наступления какого-либо события, срок, затраты и т.д.) говорят о применении точечных оценок.

В этом случае, если x_ij - точечная оценка, данная i-м экспертом j-му объекту, групповая точечная оценка определяется как

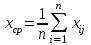(9.2)

9.3. Обработка и анализ экспертных оценок
После получения оценок производится оценка согласованности действий экспертов и определение тесноты связи между оценками. Для определения согласованности оценок 2-х экспертов используют коэффициент Спирмена:
При строгом ранжировании используют следующую формулу:
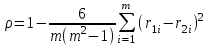(9.3)
где, m- число экспертов, r_1i- ранг 1-го эксперта, r_2i- ранг 2-го эксперта.

При нестрогом ранжировании используют такую методику определения данного коэффициента:

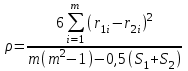(9.4)

где S_i определяется как:

(9.5)

где k- количество групп одинаковых рангов в оценке i-го эксперта, t_ik – количество одинаковых рангов в i-й группе.
Если коэффициент Спирмена равен 0, считается, что оценки некорректны (независимы). Если он равен +1, то оценки одинаковы, если –1, противоположны.

В теории математической статистики доказано, что если число факторов больше 10, то распределение величины

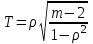(9.6)

соответствует распределению Стьюдента с m-2 степенями свободы. По таблица распределения Стьюдента определяют значение t_кр при уровне значимости 0,05 и количестве степеней свободы m-2. Если вычисленное по формуле значение T>t_кр считают, что полученные экспертные оценки связаны с действующими закономерностями, и не являются случайными.
Пример 7.2. Для решения задачи повышения рентабельности предприятия 2 эксперта предложили использовать 6 мероприятий:

Закупка более качественного сырья

Создание премиального фонда

Модернизация оборудования

Повышение квалификации рабочих

Сокращение управленческого аппарата

Закупка лицензий
Результаты ранжирования приведены в таблице:

1 эксп	1	5,5	2,5	2,5	5,5	4
2 эксп	1	6	4,5	2	4,5	3

Определить степень согласованности экспертов.
Решение:

Ранжирование нестрогое. Поэтому необходимо производить вычисления в несколько этапов:

1. 
   Определим значения S₁ и S₂:
   

В оценках первого эксперта имеются две группы одинаковых рангов, в каждой из которых по две одинаковые оценки. У второго эксперта только одна группа одинаковых рангов. Поэтому:

S₁=(2^2-2)+(2^2-2)=12

S₂=(2^2-2)=6

2. 
   Определим значение коэффициента Спирмена:
   

=(6*(1-1)^2+(5,5-6)^2+(2,5-4,5)^2+(2,5-2)^2+(5,5-4,5)^2+(4-3)^2))/(6*(6^2-1)-0,5*(12+6))=0,19

Значение коэффициента Спирмена ближе к нулю, чем к единице, значит, можно считать, что оценки этих экспертов несогласованы.
Для оценки согласованности действий более чем двух экспертов используют коэффициент конкордации Кендалла.
При строгом ранжировании этот критерий вычисляется по формуле:

, где (9.7)

где n- число экспертов;

m - число оцениваемых факторов;

r_ij- ранг j-го элемента, оцененного i-м экспертом.
При нестрогом ранжировании он рассчитывается в соответствии со следующими формулами:




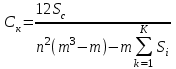
(9.8)
где Si – это величина, учитывающая число типов связанных рангов в строке, которая определяется как:




,

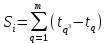
t_q – количество одинаковых рангов одного типа.



По рассчитанному таким образом значению коэффициента конкордации Кендалла определяют значение критерия Пирсона ² по формуле:

²=С_к*m*(n-1)

и сравнивают с критическим значением, полученным по таблице распределения Пирсона. Если ²<²_кр (критическое значение критерия Пирсона определяется при числе степеней свободы m-1 и уровне значимости 0,05), то говорят, что согласованность экспертных оценок низкая.
Пример 9.3. При опросе 5 экспертов были получены следующие нестрогие ранжировки. для 10 факторов:

	1факт	2 факт	3 факт	4 факт	5 факт	6 факт	7 факт	8 факт	9 факт	10 факт
1 экс	1	2	3,5	9,5	5	6	7,5	7,5	9	10
2 эксп	1,5	1,5	3,5	3,5	5	7	7	7	9,5	9,5
3 эксп	2	1	3,5	3,5	5,5	5,5	8	7	9,5	9,5
4 эксп	10	9	8	6,5	6,5	5	3	4	1	2
5 эксп	9,5	9,5	7	8	5,5	5,5	4	2,5	2,5	1

Определить степень согласованности экспертов.
Решение:

Так как в таблице представлены результаты нестрогого ранжирования используем формулы 7.7:
1. Определим среднее значение суммы ранговых оценок: 5*(10+1)/2=27,5
2. Определим сумму рангов по каждому столбцу:

	1факт	2 факт	3 факт	4 факт	5 факт	6 факт	7 факт	8 факт	9 факт	10 факт
1 экс	1	2	3,5	3,5	5	6	7,5	7,5	9	10
2 эксп	1,5	1,5	3,5	3,5	5	7	7	7	9,5	9,5
3 эксп	2	1	3,5	3,5	5,5	5,5	8	7	9,5	9,5
4 эксп	10	9	8	6,5	6,5	5	3	4	1	2
5 эксп	9,5	9,5	7	8	5,5	5,5	4	2,5	2,5	1
Сумма	24	23	25,5	31	27,5	29	29,5	28	31,5	32

3. Определим сумму квадратов отклонений от средних сумм ранговых оценок:

S_c=(24-27,5)²+(23-27,5)²+(25,5-27,5)²+(31-27,5)²+(27,5-27,5)²+(29-27,5)²+(29,5-27,5)² +(28-27,5)²+(31,5-27,5)²(32-27,5)²=91,5
4. Определим значение S_i которое учитывает связанные ранги:

Например, в первой строке 2 одинаковых ранга 3,5 и два одинаковых ранга 7,5. значит, S₁=(2³-2)+(2³-2)=12, во второй строке два одинаковых ранга 1,5, два одинаковых ранга 3,5, 3 одинаковых ранга 7 и 2 одинаковых ранга 9,5. Потому S₂=(2²-2)+(2³-2)+(3³-3)+(2³-2)=42 и т.д.

	1факт	2 факт	3 факт	4 факт	5 факт	6 факт	7 факт	8 факт	9 факт	10 факт	Si
1 экс	1	2	3,5	3,5	5	6	7,5	7,5	9	10	12
2 эксп	1,5	1,5	3,5	3,5	5	7	7	7	9,5	9,5	42
3 эксп	2	1	3,5	3,5	5,5	5,5	8	7	9,5	9,5	12
4 эксп	10	9	8	6,5	6,5	5	3	4	1	2	6
5 эксп	9,5	9,5	7	8	5,5	5,5	4	2,5	2,5	1	18
Сумма	24	23	25,5	31	27,5	29	29,5	28	31,5	32	96

5. Определим значение коэффициента конкордации:

С_к=(12*91,5)/(5²*(10³-10)-10*96)=0,0046

6. 
   Определяем значение ²=0,046*5*9=2,07
   

7. 
   Табличное значение критерия Пирсона при при уровне значимости 0,95 и числе степеней свободы 9 равно 16,92. Следовательно, можно сделать вывод о том, что оценки экспертов несогласованы.