УвОС. РАЗДЕЛ 9. 9 Область применения и сущность экспертных методов
 Скачать 81.99 Kb. Скачать 81.99 Kb.
|
1 2 9.4. Метод анализа иерархий (МАИ) 9.4.1 Сущность метода. Метод анализа иерархий (МАИ)– один из наиболее универсальных современных методов поддержки принятия управленческих решений, основанных на получении и анализе экспертных оценок. Он применяется для выбора одной из множества альтернатив, которые необходимо оценить с точки зрения выполнения нескольких критериев, так, чтобы выполнялось несколько целей. Метод был предложен Т. Саати. Сейчас МАИ используется повсеместно – в риэлтерском деле, в кадровых службах, при оценке инвестиционных проектов и т.д. Сущность метода состоит в декомпозиции проблемы на все более простые составляющие, которые оцениваются экспертами, в результате чего получается интегрированная оценка каждой альтернативы Основные этапы. Структурирование проблемы в виде иерархии. Иерархия строится следующим образом: 1 уровень – цель решения проблемы, с точки зрения задач управления; 2 уровень (необязательно) – подцели, выполнение которых приводит к выполнению главной цели; 3 уровень – критерии, по которым будут оцениваться альтернативы; 4 уровень – альтернативы. На основании экспертного опроса строятся матрицы попарных сравнений для элементов каждого из уровней, начиная со второго, с точки зрения элементов предыдущего уровня. Для каждой полученной матрицы определяется собственный вектор и индекс согласованности, позволяющий определить соответствие экспертных оценок в разных матрицах. Проблема связана с тем, что эксперт, сравнивая альтернативы попарно, не обязан думать о взаимоотношениях этих альтернатив со всеми остальными. При этом могут возникнуть нарушения транзитивности суждений, которые делают бессмысленной дальнейшую обработку матриц. В данном методе обосновано, что индекс несогласованности ИС не должен превышать значения 0.1. Заключительным этапом метода является синтез приоритетов. Синтез приоритетов заключается во взвешивании собственного вектора матриц на каждом уровне компонентами собственного вектора вышележащего уровня. 9.4.2.Пример применения МАИ Пусть необходимо выбрать город, в котором будет открыт филиал фирмы с точки зрения достижения ее целей. 1 этап. Построение иерархии Главная цель – успех фирмы Подцели: повышение прибыли (ПЦ1) рост доли рынка (ПЦ2) Критерии: производственные площади (К1) персонал (К2) транспортные развязки (К3) капитал (К4) покупательский спрос (К5) Альтернативы: Город А, Город В, Город С. 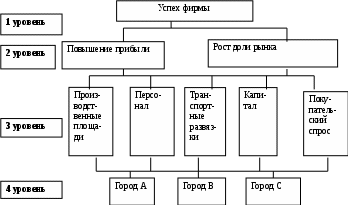 Рис. 9.1 Рис. 9.1Вводится оценочная шкала, руководствуясь которой, эксперты будут оценивать превосходство одного параметра над другим.
2 и 3 этапы. Построение матриц попарных сравнений и оценка их согласованности. Эксперты сравнивают подцели, с точки зрения выполнения главной цели.
Заполняются только ячейки над главной диагональю каждой матрицы. Ячейки под главной диагональю соответствуют обратным значениям. Определяем собственный вектор: Определим нормализованную матрицу путем деления каждого элемента столбца на сумму элементов по этому столбцу Определим собственный вектор каждой матрицы путем определения среднего по каждой строке нормализованной матрицы.
Эксперты сравнивают важность критериев с точки зрения подцели Повышение прибыли
Определяем собственный вектор:
Определяем индекс согласованности: Определяем L : Для этого находим сумму произведений сумм по столбцам исходной матрицы и элементов собственного вектора. Определяем ИС=(L-n)/(n-1)
Эксперты сравнивают важность критериев с точки зрения подцели Завоевание доли рынка
Собственный вектор:
Индекс согласованности:
Данный индекс превышает 0,1, следовательно, эксперт должен пересмотреть матрицу попарных сравнений, чтобы устранить нарушение транзитивности оценок. Новая матрица:
Собственный вектор:
Индекс согласованности для нее равен 0,1. Эксперты сравнивают альтернативы по каждому из критериев: По критерию Производственные площади: По критерию Персонал
По критерию Транспортные развязки По критерию Капитал
По критерию Покупательский спрос
Выполним численную обработку полученных матриц. Собственные векторы приведенных выше матриц:
Для каждой матрицы получим:
4 этап: Синтез приоритетов. Синтез приоритетов заключается во взвешивании собственного вектора матриц на каждом уровне компонентами собственного вектора вышележащего уровня. Уровень подцелей не взвешивается Взвесим собственные векторы матриц критериев относительно уровня подцелей ( 0,68*0,07+0,33*0,09 =0,08 и т.д:
Для уровня альтернатив полу чим взвешенные оценки относительно уровня критериев :
Взвешенные оценки городов, с учетом выполнения подцелей и критериев следующие:
Вывод: С учетом выполнения целей, по совокупности критериев, наиболее эффективным окажется строительство филиала в городе А. 1 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
