Иллюстрация на тему «Современный взгляд на окружающую действительность». 9 задание теория вероятности. Ответ не может быть больше 1 13 задание
 Скачать 34.4 Kb. Скачать 34.4 Kb.
|
|
9 задание: теория вероятности. 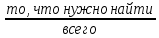 Ответ не может быть больше 1 13 задание:  Формулы сокращенного умножения: 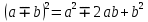 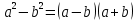 Признаки делимости (необходимо для сокращения и подбора нового знаменателя) Признак делимости на 2 Последняя цифра числа должна быть четной - 0,2,4,6,8 Признак делимости на 3 Сумма цифр в данном числе должна быть кратна 3 Признаки делимости на 5 Последняя цифра должна быть 0 или 5 Признак делимости на 9 Сумма цифр в данном числе должна быть кратна 9 Признак делимости на 10 Последняя цифра должна быть 0 Разделить на 10, 100, 1000 и т.д, значит перенести запятую на столько знаков влево, сколько нулей в делителе (пример 256:10000=0,0256; 3,7:10=0,37) Свойства степеней an • ak = an+k 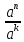 = an−kили an : ak = an−k = an−kили an : ak = an−ka0 =1 (an)k = ank am × bm = (ab)m am ÷ bm= 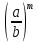 Стандартный вид числа: записать число цифрами, поставить запятую после первого числа, сосчитать количество цифр после запятой и записать 10 в той степени сколько цифр после запятой. Пример: 173 тыс= 173000=1,73·105 Любое квадратное уравнение ( степень у икса 2) можно решить через дискриминант (D= b2-4ac, x1,2=  ) )Теорема Виета (применяется когда коэффициент а =1) : 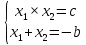 Неполные квадратные уравнения: 1 вид: ax2+bx=0 – неполное квадратное уравнение (с=0). Решение: x (ax+b)=0 x1=0 или ax+b=0 x2=-b/a. Ответ: 0; -b/a. 2 вид: ax2-c=0 – неполное квадратное уравнение (b=0); Решение: ax2=c x2=c/a. Если (c/a)<0, то действительных корней нет. Если (с/а)>0, то имеем два действительных корня: x1= 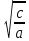 x2= - x2= -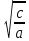 Неравенства: Линейные неравенства решение: 1.с неизвестным в одну сторону, число в др. знак неравенства сохраняется. Знак неравенства меняется, если делим обе части неравенства на отрицательное число. 2.чертим координатную прямую, отмечаем точки в порядке возрастания. Точки пустые если знак неравенства 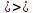 , точки жирные если знак неравенства , точки жирные если знак неравенства 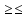 , заштриховываем нужные ответ по знаку неравенства. , заштриховываем нужные ответ по знаку неравенства. 3.Записываем ответ. Если точка пустая или бесконечность -- скобки круглые, точка жирная -- скобка квадратная. Квадратные неравенства: Переписываем уравнение, заменяя знак неравенства на знак равно. Решаем квадратное уравнение любым известным способом. На координатной прямой расставляем точки в порядке возрастания (пустые или жирные) В любом из полученных интервалов берем любую удобную для счета точку, подставляем в уравнение, в правой части которого 0, Определяем знак на промежутке. Расставляем знаки на оставшихся интервалах. Выбираем нужный соответствовав знаку неравенства Записываем ответ. Если точка пустая или бесконечность -- скобки круглые, точка жирная -- скобка квадратная. Решение системы неравенств: Решаем отдельно первое неравенство из системы. Решаем отдельно второе неравенство из системы. На одной координатной прямой отмечаем получившиеся точки из первого и второго решения в порядке возрастания. 4. Согласна знаку неравенства сверху штрихуем решение первого неравенства, решение второго неравенства. 5. Там где штриховка совпала (снизу и сверху) есть решение всей системы неравенств. Если совпадений нет, то решений системы нет) |
