вариант 16. А. А. Воронов (инициалы, фамилия)
 Скачать 124.5 Kb.
|
|
Минобрнауки России федеральное государственное бюджетное образовательное учреждение высшего образования «Санкт-Петербургский государственный технологический институт (технический университет)» ЗАДАНИЕ __________________________________________________________________ (виды работы: отчет, эссе, статья и т.д.)
Учебный модуль Теория анализа и статистика Курс 1 Группа 606зэ-22 Студент Хожаева Умидахон Улугбековна(Ф.И.О.) Цель работы ___________________ Исходные данные Вариант 8 Дата выдачи задания ________________
Вариант 16. Завод производит двигатели, которые либо сразу могут потребовать дополнительной регулировки (в 40 % случаев), либо сразу могут быть использованы (в 60 % случаев). Как показывают статистические исследования, те двигатели, которые изначально требовали регулировки, через месяц потребуют дополнительной регулировки в 65 % случаев, а в 35 % будут работать хорошо. Те же двигатели, которые не требовали первоначальной регулировки, через месяц потребуют ее в 20 % случаев, а в 80 % будут продолжать хорошо работать. Какова доля двигателей, которые будут работать хорошо или потребуют регулировки через два и три месяца после выпуска соответственно? Решение В момент после выпуска доля хороших двигателей составляет 0,6, а доля требующих регулировки – 0,4. Через месяц доля хороших составит: 0,6.0,8+0,4.0,35=0,62. Доля требующих регулировки: 0,6.0,2+0,4.0,65=0,38. введём строку состояния Xt в момент t; Xt=(x1t; x2t), где x1t – доля хороших двигателей, x2t – доля двигателей, требующих регулировки в момент t. Матрица перехода  , где  - доля двигателей, которые в настоящее время находятся в состоянии  ( 1- «хороший», 2- «требует регулировки»), а через месяц – в состоянии  .Очевидно, что для матрицы перехода сумма элементов каждой строки равна 1, все элементы неотрицательны. Очевидно,  =(0,6 0,4),  .Тогда через месяц   ,через 2 месяца  ; через 3 месяца  .Найдём матрицы  ; .Отметим, что если  - матрица перехода, то  - тоже матрица перехода при любом натуральном t. Теперь   , .Очевидно,  .Структурная матрица торговли трех стран S1, S2, S3 имеет вид А =  Найти соотношение национальных доходов стран для сбалансированной торговли. Решение Найдем собственный вектор х , отвечающий собственному значению λ=1, решив уравнение (А-Е)Х=0 или систему 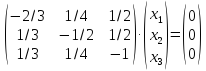 методом Гаусса.Найдем    , т.е.х = ( ).Полученный результат означает, что сбалансированность торговли трех стран достигается при векторе национальных доходов х = ( ) т.е. при соотношении национальных доходов стран 3/2:2:1 или 3:4:2.Зависимость между стоимостью единицы продукции y(тыс.руб.) и выпуском продукции x (млн.руб.) выражается функцией y=-0,5x+80. Найти эластичность себестоимости при выпуске продукции, равном 30 млн.руб. Решение По формуле эластичности себестоимости Ex(y) =(-0,5x)/(-0,5x+80) = x/(x-160). При x = 30 Ex=30(y) = -(3/13), т.е. При выпуске продукции, равном 30 млн. руб., увеличение его на 1% приведет к снижению себестоимости на (3/13)%. Производственная функция равна  , стоимость единицы первого ресурса равна 5, второго – 10. В силу бюджетных ограничений на ресурсы может быть потрачено не более 600ден. ед. В этих условиях найти оптимальное для производителя значение (х, у)количества используемых ресурсов.Решение Теперь следует максимизировать функцию  , но при условии, что  . В предыдущей задаче было найдено оптимальное распределение ресурсов в ситуации, когда ограничения отсутствовали. Оказалось, что оптимальные затраты на ресурсы равны  . Можно показать, что в этом случае в условиях наличия ограничений на ресурсы следует потратить всю возможную сумму.Итак, имеем задачу максимизации функции при условии, что 5х + 10у = 600, или х + 2у = 120. Первый способ. В силу ограничений имеем х = 120 – 2у и  .Производная функции  . Приравнивая ее к нулю, получим решение у = 24, откуда  . Максимальная прибыль при этом равна  (ден. ед.).Второй способ. При условии, что 5х + 10у = 600, функция прибыли имеет вид  . Очевидно, что если какое-то значение С уровня функции  должна пересекаться с прямой 5x + 10y = 600.Уравнение линии уровня функции прибыли  может быть записано как  , где  .Легко видеть, что максимальное значение А,а следовательно, и уровня С достигается в том случае, если соответствующая линия уровня касается прямой 5х + 10у = 600. Так как градиент в каждой точке ортогонален линии уровня, то из этого следует, что условие максимальности прибыли может быть сформулировано следующим образом: вектор 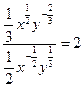 ортогонален прямой 5х + 10у = 600. Эта прямая имеет угловой коэффициент, равный  . Угловой коэффициент прямой, проходящей через вектор равен  . По условию перпендикулярности прямых имеем  , т.е.  или  . Подставляя полученное выражение в уравнениепрямой  , находим х = 72, у = 24.Изменение численности населения горнорудного поселка с течением времени описывается следующим уравнением: 𝑦′ = 0,3 ∙ 𝑦 ∙ (2 − 10−4 ∙ 𝑦), где 𝑦 = 𝑦(𝑡); 𝑡 – время в годах. В начальный момент времени население поселка составляло 500 человек. Каким оно станет через три года? Решение Разделяя переменные в уравнении, приходим к равенству:  Выполняя почленное интегрирование этого равенства, получаем 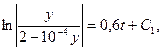 или  (5.1)Значение постоянной С находим из начальных условий: так как y(0) = 500, то С ≈ 256,4. Выражая теперь функцию y из (5.1), получаем  Тогда  |