А аддитивная модель ряда динамики представляет собой в величина, рассчитанная по формуле является оценкой
 Скачать 99.94 Kb. Скачать 99.94 Kb.
|
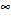 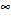 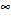 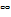 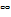 А ААддитивная модель ряда динамики представляет собой: 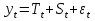 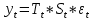 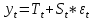 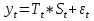 В Величина, рассчитанная по формуле 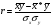 является оценкой является оценкойкоэффициента детерминации частного коэффициента корреляции парного коэффициента корреляции множественного коэффициента корреляции Верификация модели — это: определение вида экономической модели, выражение в математической форме взаимосвязи между ее переменными определение исходных предпосылок и ограничений модели анализ изучаемого экономического явления проверка истинности, адекватности модели В каких пределах изменяется коэффициент детерминации от –1 до 0 от 0 до 1 от –1 до 1 от 0 до 10 В каких пределах изменяется множественный коэффициент детерминации? -1< 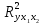 < 1 < 1- < 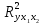 <1 <10 < 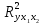 <1 <11 < 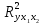 < < В каких пределах изменяется множественный коэффициент корреляции от –1 до 0 от 0 до 1 от –1 до 1 от 0 до 10 В каких пределах изменяется множественный коэффициент корреляции: -1< 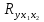 < 1 < 10 < 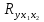 < 1 < 10 < 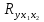 < < - < 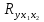 < < В модели множественной линейной регрессии высокая корреляция между двумя объясняющими переменными приводит к: несостоятельности оценок коэффициентов, полученных по методу наименьших квадратов неэффективности оценок коэффициентов, полученных по методу наименьших квадратов значительной дисперсии оценок коэффициентов, полученных по методу наименьших квадратов невозможности определения изолированного влияния регрессоров на зависимую переменную и однозначной их интерпретации равенству нулю оценок коэффициентов, полученных по методу наименьших квадратов В правой части приведенной формы взаимозависимой системы могут стоять Эндогенные лаговые и экзогенные переменные (как лаговые, так и нелаговые) Только экзогенные лаговые переменные Только экзогенные переменные (как лаговые, так и нелаговые) Только эндогенные переменные (как лаговые, так и нелаговые) Любые экзогенные и эндогенные переменные В правой части приведенной формы системы одновременных уравнений не могут стоять Экзогенные лаговые переменные Эндогенные переменные Экзогенные переменные (как лаговые, так и нелаговые) Эндогенные лаговые переменные Все ответы верны Все ответы не верны В правой части структурной формы взаимозависимой системы могут стоять Только экзогенные лаговые переменные Только экзогенные переменные (как лаговые, так и нелаговые) Только эндогенные лаговые переменные Любые экзогенные и эндогенные переменные Только эндогенные переменные (как лаговые, так и нелаговые) В правой части структурной формы взаимозависимой системы не могут стоять Экзогенные лаговые переменные Экзогенные переменные (как лаговые, так и нелаговые) Эндогенные лаговые переменные Эндогенные переменные Все ответы верны Все ответы не верны В регрессионном анализе xj рассматриваются как случайные величины любые величины дробные величины неслучайные величины В уравнении линейной парной регрессии параметр b, означает: усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов; среднее изменение результативного признака при изменении факторного признака на 1% на какую величину в среднем изменится результативный признак у, если переменную х увеличить на единицу измерения какая доля вариации результативного признака у учтена в модели и обусловлена влиянием на нее переменной х В формуле 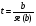 число b это число b это случайный член коэффициент регрессии независимая переменная зависимая переменная В формуле 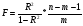 число m это число m это количество оцениваемых коэффициентов в функции регрессии количество предопределённых переменных в функции регрессии число независимых переменных модели количество наблюдений В хорошо подобранной модели остатки должны (выберите необходимые пункты) иметь нормальный закон распределения с нулевым математическим ожиданием и постоянной дисперсией не коррелировать друг с другом иметь экспоненциальный закон распределения хаотично разбросаны форма и вид распределения не важен Выберите аналог понятия «независимая переменная»: Фактор эндогенная переменная экзогенная переменная регрессор результат Выберите аналог понятия «эндогенная переменная»: Результат фактор зависимая переменная, определяемая внутри системы предопределенная переменная Выборочный коэффициент корреляции r по абсолютной величине не превосходит нуля принимает любые значения не превосходит единицы не превосходит 10 Д Дана следующая макроэкономическая модель: Y = C + I + G - макроэкономическое тождество C = α +βY + U1 - функция потребления I =γ – µ∙R + δY + U2 - функция инвестиций M = ηY – λR + U3 - уравнение денежного рынка где эндогенными переменными являются доход Y, потребление C, инвестиции I и процентная ставка R. Переменные G (государственные расходы) и (M) (реальная денежная масса) – экзогенные. Выберите верное утверждение из следующих. функция инвестиций неидентифицируема функция потребления неидентифицируема функция инвестиций однозначно идентифицируема функция потребления однозначно идентифицируема функция инвестиций сверхидентифицируема Дана следующая макроэкономическая модель: Y = C + I + G - макроэкономическое тождество C = α +βY + U1 - функция потребления I =γ – µ∙R + δY + U2 - функция инвестиций M = ηY – λR + U3 - уравнение денежного рынка где эндогенными переменными являются доход Y, потребление C, инвестиции I и процентная ставка R. Переменные G (государственные расходы) и (M) (реальная денежная масса) – экзогенные. Выберите верное утверждение из следующих. функция инвестиций неидентифицируема функция потребления сверхидентифицируема функция потребления неидентифицируема функция потребления однозначно идентифицируема функция инвестиций сверхидентифицируема Для вычисления прогноза значения эндогенной переменной в рамках модели множественной регрессии нужно знать значение случайного возмущения, u значение эндогенной переменной Y значения экзогенных переменных значения экзогенных и эндогенной переменных Для оценки структурных коэффициентов целесообразно использовать Двухшаговый метод наименьших квадратов Обычный метод наименьших квадратов Обобщенный метод наименьших квадратов Косвенный метод наименьших квадратов Нецелесообразно использовать ни один из перечисленных методов Е Если коэффициент корреляции отрицателен, то в парной линейной модели с ростом х увеличивается у с уменьшением х уменьшается у с ростом х уменьшается у x и y независимы Если коэффициент корреляции положителен, то в парной линейной модели с ростом х уменьшается у с уменьшением х растёт у с ростом х увеличивается у x и y независимы Если коэффициент уравнения регрессии (k ) статистически значим, то k > 1 k 0 |k | > 1 k > 0 Ни один из ответов не верен Если парный коэффициент корреляции между признаками Y и X принимает значение 0,675, то коэффициент детерминации равен: -67,5 45,6 82,2 57,6 Если парный коэффициент корреляции между признаками Y и X равен «-1», то это означает: отсутствие связи наличие обратной корреляционной связи наличие обратной функциональной связи наличие прямой функциональной связи Если структурные коэффициенты модели выражены через приведенные коэффициенты и имеют более одного числового значения, то такая модель: сверхидентифицируемая неидентифицируемая идентифицируемая рекурсивная З Зависимость между коэффициентами множественной детерминации (D) и корреляции (R) описывается следующей формулой: R2 = 1–D2 D2=1–R2 D= R R= D Ни одной из формул Значение параметра b в уравнении линейной парной регрессии определяется по формуле: 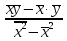 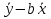 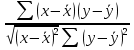 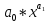 Значимость линейного коэффициента корреляции проверяется с помощью F – критерия нормального закона распределения t-критерия Стьюдента Критерия Дарбина-Уотсона И Из перечисленных моделей выберите регрессионные модели с одним уравнением: 1) модель цены от объема поставки; 2) модель спроса и предложения; 3) модель тренда и сезонности; 4) модель зависимости объема производства от производственных факторов: 2, 4 2, 3 1,4 Все Имеется матрица парных коэффициентов корреляции:
Между какими признаками наблюдается мультиколлинеарность: y и x3 x2 и x x1 и x33 мультиколлинеарность отсутствует Имеются следующие данные: коэффициент регрессии b = 1,341: стандартная ошибка коэффициента регрессии se(b) = 0,277. Определите t-критерий Стьюдента и оцените значимость коэффициента регрессии b, если tта6л =2,11 при уровне значимости 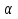 = 0,05. = 0,05.0,207, коэффициент незначим 4,841, коэффициент значим 4,841, коэффициент незначим 0,372, коэффициент значим Индекс корреляции определяется по формуле: 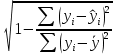 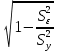 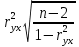  К Какая задача эконометрики является задачей параметризации модели: выбор вида функции, спецификация модели, формулировка исходных предпосылок и ограничений модели составление прогноза и рекомендаций для конкретных экономических явлений по результатам эконометрического моделирования оценка параметров построения модели построение эконометрических моделей для эмпирическое анализа Как в степенной модели интерпретируется коэффициент регрессии b? тангенс угла наклона регрессии значение результативного признака при нулевом значении фактора коэффициент эластичности доля изменчивости зависимой переменной Как интерпретируется в парной линейной модели коэффициент регрессии а? значение результативного признака при нулевом значении фактора коэффициент эластичности тангенс угла наклона регрессии доля изменчивости зависимой переменной Как интерпретируется в парной линейной модели коэффициент регрессии b коэффициент эластичности значение результативного признака при нулевом значении фактора тангенс угла наклона регрессии доля изменчивости зависимой переменной Какова цель эконометрики: определить способы сбора и группировки статистических данных разработать способы моделирования и количественного анализа реальных экономических объектов представить экономические данные в наглядном виде изложить в математической формулировке экономические законы Какое значение может принимать множественный коэффициент корреляции: -0,453 -1,72 0,861 1,501 Какое значение не может принимать парный коэффициент корреляции: -0,973 0,005 0,721 1,111 Какое из уравнений регрессии нельзя свести к линейному виду: 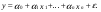 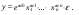  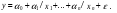 все уравнения можно свести к линейному виду. Какое из уравнений регрессии является показательным? 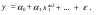 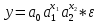 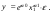 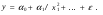 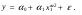 Какое из уравнений регрессии является степенным: 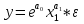 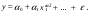 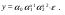 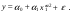 ни одно из уравнений не является степенным Какое определение соответствует понятию «эконометрика»: это наука, предметом изучения которой является количественная сторона массовых социально-экономических явлений и процессов в конкретных условиях места и времени это наука, предметом изучения которой являются общие закономерности случайных явлений и методы количе ственной оценки влияния случайных факторов это наука, предметом изучения которой является количественное выражение взаимосвязей экономических явлений и процессов это наука, предметом изучения которой являются модели экономических объектов и процессов и методы их исследования Какое предположение о векторе случайной составляющей не является предпосылкой классической регрессионной модели: случайная составляющая имеет постоянную дисперсию (свойство гомоскедастичности) отсутствует автокорреляция случайной составляющей случайная составляющая обладает нормальным распределением все предположения являются предпосылками классической модели случайная составляющая имеет нулевое математическое ожидание Какое предположение о матрице факторов Х не является предпосылкой классической линейной регрессионной модели. матрица факторов Х – невырожденная (независимые переменные не коррелируют друг с другом длина исходного ряда данных больше, чем количество факторов (достаточное число степеней свободы) независимые переменные экзогенны матрица факторов Х содержит все важнейшие факторы, определяющие изменения зависимой переменной все предположения являются предпосылками классической регрессионной модели. Какое предположение о результирующем показателе является предпосылкой классической регрессионной модели: результирующий показатель измеряется в порядковой шкале результирующий показатель измеряется в номинальной шкале результирующий показатель измеряется в дихотомической (бинарной) шкале результирующий показатель является количественным, причем на него не накладываются особые ограничения ни одно из предположений не является предпосылкой классической регрессионной модели Какой коэффициент определяет среднее изменение результативного признака при изменении факторного признака на 1%: коэффициент регрессии коэффициент детерминации коэффициент корреляции коэффициент эластичности Какой коэффициент указывает в среднем процент изменения результативного показателя Y при увеличении аргумента х на 1%: коэффициент эластичности коэффициент детерминации коэффициент регрессии бета-коэффициент Какой критерий используют для оценки значимости коэффициента корреляции: F-критерий Фишера критерий Пирсона t-критерий Стьюдента d-критерий Дарбина—Уотсона Какой критерий используют для оценки значимости урав нения регрессии: критерий Пирсона F- критерий Фишера t-критерий Стьюдента d-критерий Дарбина—Уотсона Какую модель следует выбрать, если есть основания считать, что в изучаемом периоде коэффициент абсолютного прироста не изменяется? показательную степенную линейную экспоненциальную Какую модель следует выбрать, если есть основания считать, что в изучаемом периоде коэффициент эластичности не изменяется? степенную линейную показательную экспоненциальную Какую модель следует выбрать, если есть основания считать, что в изучаемом периоде цепные коэффициенты роста не изменяются? экспоненциальную линейную показательную степенную Квадрат какого коэффициента в парной регрессии указывает долю дисперсии одной случайной величины, обусловленную вариацией другой коэффициент детерминации частный коэффициент корреляции парный коэффициент корреляции множественный коэффициент корреляции Количество структурных и приведенных коэффициентов одинаково в модели: идентифицируемой сверхидентифицируемой неидентифицируемой рекурсивной Коэффициент детерминации показывает Тесноту связи между фактическими и расчетными значениями результирующего показателя в базисном периоде Статистическую значимость модели в целом на основе определения совокупной достоверности всех ее коэффициентов Долю изменчивости зависимой переменной, объясненную влиянием факторов, включенных в модель Экономическую значимость модели в целом Ни одно из высказываний не верно Коэффициент детерминации это квадрат частного коэффициента корреляции квадрат коэффициента регрессии квадрат коэффициента корреляции квадрат коэффициента эластичности Коэффициент корреляции, равный нулю, означает, что между переменными существует линейная связь ситуация не определена не существует связи линейная связь отсутствует Коэффициент наклона линии регрессии всегда находится от –1 до 1 никогда не бывает отрицательным равен коэффициенту корреляции может принимать любое значение не может быть равен нулю Коэффициент регрессии в линейной регрессии совокупного спроса на мобильные телефоны (в тысячах рублей) по цене (в рублях) оказался равным «–1». Это означает, что увеличение цены на 1% снижает спрос на мобильные телефоны на 1% увеличение цены на 1 рубль снижает спрос на мобильные телефоны на 1% увеличение цены на 1 рубль снижает спрос на мобильные телефоны на одну тысячу рублей увеличение цены на 1% снижает спрос на мобильные телефоны на одну тысячу рублей полученное число никак не интерпретируется Коэффициент регрессии в линейной регрессии совокупного спроса на стулья (в тысячах рублей) по цене (в тыс.рублях) оказался равным «–2». Это означает, что увеличение цены на 1% снижает спрос на стулья на 2% увеличение цены на 1 рубль снижает спрос на стулья на 2% увеличение цены на 1% снижает спрос на стулья на две тысячи рублей увеличение цены на 1 тысячу рублей снижает спрос на стулья на две тысячи рублей полученное число никак не интерпретируется Коэффициент регрессии изменяется в пределах от –1 до 1 0 до 1 принимает только целые значения принимает любое значение Коэффициент уравнения регрессии показывает На сколько % изменится результат при изменении фактора на 1 % На сколько % изменится фактор при изменении результата на 1 % На сколько ед. изменится фактор при изменении результата на 1 ед. Во сколько раз изменится результат при изменении фактора на 1 ед. На сколько ед. изменится результат при изменении фактора на 1 ед. Коэффициент эластичности показывает На сколько ед. изменится фактор при изменении результата на 1 ед. На сколько ед. изменится результат при изменении фактора на 1 ед. На сколько % изменится результат при изменении фактора на 1 % Во сколько раз изменится результат при изменении фактора на 1 ед. На сколько % изменится фактор при изменении результата на 1 % Критерий Стьюдента используется в эконометрическом моделировании И для определения статистической значимости каждого из коэффициентов уравнения регрессии и для расчетов доверительных интервалов коэффициентов уравнения регрессии и прогнозного интервала зависимой величины Только для определения статистической значимости каждого из коэффициентов уравнения регрессии Только для определения экономической значимости каждого из коэффициентов уравнения регрессии Только для расчетов доверительных интервалов коэффициентов уравнения регрессии и прогнозного интервала зависимой величины Ни одно из высказываний не верно Критерий Дарбина-Уотсона применяется для Ни одно из высказываний не верно Определения экономической значимости модели в целом Определения статистической значимости модели в целом Сравнения двух альтернативных вариантов модели Отбора факторов в модель Критерий Стьюдента предназначен для определения экономической значимости каждого из коэффициентов уравнения регрессии определения статистической значимости каждого из коэффициентов уравнения регрессии определения статистической значимости модели в целом на основе совокупной достоверности всех ее коэффициентов определения экономической значимости регрессионной модели в целом ни одно из высказываний не верно Критерий Фишера используется для проверки гипотезы о значимости коэффициентов регрессии проверки автокоррелированности остатков проверки гипотезы о значимости уравнения регрессии в целом проверки на однородность выборок проверки на гетероскедастичность Критерий Фишера показывает Долю изменчивости зависимой переменной, объясненную влиянием факторов, включенных в модель Статистическую значимость модели в целом на основе совокупной достоверности всех ее коэффициентов Тесноту связи между фактическими и расчетными значениями результирующего показателя Экономическую значимость модели в целом Ни одно из утверждений не верно М МНК позволяет получить состоятельные и несмещенные оценки параметров системы: одновременных уравнений рекурсивных уравнений независимых уравнений Множественный линейный коэффициент корреляции 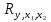 равен 0,75. Какой процент вариации зависимой переменной Y учтен в модели и обусловлен влиянием факторов х1 и х2. равен 0,75. Какой процент вариации зависимой переменной Y учтен в модели и обусловлен влиянием факторов х1 и х2.37,56 56,25 75,05 0,75 Модель в целом статистически значима, если Fф Fкр Fф Fкр Fф Fкр Fф = Fкр Ни один из ответов не верен. Мультипликативная модель ряда динамики представляет собой: 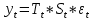 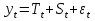 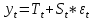 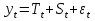 Н Набор сведений о разных объектах, взятых за один период времени, называется: пространственными данными временными данными панельными данными статистическими данными Найдите верное высказывание. Эластичность показывает: на сколько единиц изменится фактор xk при изменении результирующего показателя y на 1 единицу на сколько единиц изменится результирующий показатель y при изменении фактора xk на 1 единицу на сколько % изменится результирующий показатель y при изменении фактора xk на 1 % на сколько % изменится фактор xk при изменении результирующего показателя y на 1 % все высказывания неверны Найдите правильную последовательность этапов эконометрического моделирования: постановочный, априорный, информационный, параметризации, идентификации, верификации информационный, постановочный, априорный, параметризации, верификации, идентификации постановочный, априорный, параметризации, информационный, идентификации, верификации Найдите правильную последовательность шагов алгоритма применения двухшагового МНК: 1) Преобразование структурной формы модели в приведенную 2) Процесс оценки параметров приведенной формы с помощью МНК 3) Получение по соответствующим приведенным уравнениям теоретических значений эндогенных переменных правой части сверхидентифицируемого уравнения модели 4) Процесс оценки параметров сверхидентифицируемого уравнения модели через теоретические значения эндогенных и фактические значения предопределенных переменных 1) Получение по соответствующим приведенным уравнениям теоретических значений эндогенных переменных правой части сверхидентифицируемого уравнения модели 2) Процесс оценки параметров сверхидентифицируемого уравнения модели через теоретические значения эндогенных и фактические значения предопределенных переменных 3) Преобразование структурной формы модели в приведенную 4) Процесс оценки параметров приведенной формы с помощью МНК 1) Процесс оценки параметров приведенной формы с помощью МНК 2) Получение по соответствующим приведенным уравнениям теоретических значений эндогенных переменных правой части сверхидентифицируемого уравнения модели 3) Процесс оценки параметров сверхидентифицируемого уравнения модели через теоретические значения эндогенных и фактические значения предопределенных переменных 4) Преобразование структурной формы модели в приведенную Найдите предположение, являющееся предпосылкой классической модели. Результирующий показатель измеряется в порядковой шкале Результирующий показатель измеряется в номинальной шкале Результирующий показатель измеряется в дихотомической шкале Результирующий показатель является количественным Результирующий показатель может быть и количественным и качественным Найдите приведенную форму, соответствующую структурной форме модели 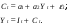 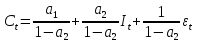 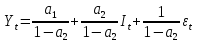  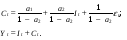  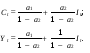 На основании рядов данных для переменных X и Y построено уравнение регрессии: 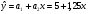 . Какое из следующих высказываний является верным: . Какое из следующих высказываний является верным:оценка коэффициента a2 =1,25 означает, что если значение переменной Х увеличится в среднем на 1,25, то значение переменной Y при прочих равных условиях увеличится на 1 единицу оценка коэффициента a2 =1,25 означает, что если значение переменной Y увеличится на 1 единицу, то значение переменной X при прочих равных условиях увеличится в среднем на 1,25 если при прочих равных условиях значение переменной Х удвоится, то значение переменной Y возрастет в среднем на 25% все высказывания неверны На основании рядов данных для переменных X и Y построено уравнение регрессии: 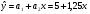 . Если х=2, то эластичность результирующего показателя y относительно фактора х : . Если х=2, то эластичность результирующего показателя y относительно фактора х :0,33 1,25 2 7,5 4,6875 Неправильный выбор функциональной формы или объясняющих переменных называется ошибками прогноза гетероскедастичностью автокорреляцией ошибками спецификации О Оценки параметров регрессии (свойства оценок МНК) должны быть: несмещенными состоятельными гетероскедатичными эффективными П По 39 точкам оценена следующая формула производственной функции, в которой отдельно рассмотрены две составляющие затрат основного капитала: K1 - здания и сооружения, и K2 - машины и оборудование; а также две составляющие затрат труда: L1 - затраты квалифицированного труда, и L2 - затраты неквалифицированного труда; Y – выпуск: ln(Y)= 4,3 + 0,35ln(K1) + 0,26ln(K2) + 0,63ln(L1) + 0,58ln(L2) (1,4) (0,03) (0,05) (0,41) (0,38); R2 =0,92; DW=1,74 (в скобках приведены стандартные ошибки коэффициентов). Какой из выводов и дальнейших шагов представляется Вам верным? Имеет место мультиколлинеарность, поэтому нужно объединить факторы K1 и K2 Имеет место мультиколлинеарность, поэтому нужно объединить факторы L1 и L2 Нужно исключить фактор L (переменные L1 и L2), т.к. он оказался незначимым Отклонения ei автокоррелированы, нужно изменить формулу зависимости Формула зависимости приемлема по всем приведенным параметрам, и изменения не нужны По аналитическому выражению различают связи: Криволинейные линейные обратные парные По данным с 1990 по 1998 гг. построено уравнение регрессии 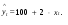 Значения фактора xt можно спрогнозировать по трендовой модели xt=1+0,2t. Рассчитайте точечный прогноз результирующего показателя yt в 2000 г. Значения фактора xt можно спрогнозировать по трендовой модели xt=1+0,2t. Рассчитайте точечный прогноз результирующего показателя yt в 2000 г.106 106,4 102,8 102,44 Ни один из ответов не верен Под частной корреляцией понимается: зависимость результативного признака и двух и более факторных признаков, включенных в исследование зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков связь между двумя признаками (результативным и факторным или двумя факторными) зависимость между качественными признаками При каком значении линейного коэффициента корреляции связь между признаками Y и X можно считать тесной (сильной): -0,111 -0,975 0,421 0,657 Применим ли метод наименьших квадратов для расчёта параметров нелинейных моделей? да к определенному классу моделей применим после специального приведения к линейному виду нет Применим ли метод наименьших квадратов для расчёта параметров показательной зависимости? нет да применим после её приведения к линейному виду путём логарифмирования в зависимости от исходных данных Применим ли метод наименьших квадратов для расчёта параметров степенной зависимости? нет да применим после её приведения к линейному виду путём логарифмирования в зависимости от исходных данных Пусть Y — товарооборот магазина, млн.руб., Х1 — торговая площадь, тыс.кв.м, Х2 — среднее количество посетителей в день, тыс. чел. 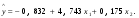 Каков будет товарооборот магазина, если он находится в относительно оживленном месте с количеством посетителей 20000 и имеет торговую площадь 1000 кв.м? Каков будет товарооборот магазина, если он находится в относительно оживленном месте с количеством посетителей 20000 и имеет торговую площадь 1000 кв.м?8242,168 млн.руб. 8,243 млн.руб. 3,911 млн.руб. 7,411 млн.руб. все ответы неверны Пусть Y — товарооборот магазина, млн.руб., Х1 — торговая площадь, тыс.кв.м, Х2 — среднее количество посетителей в день, тыс. чел. 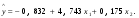 Каков будет товарооборот магазина, если он находится в относительно оживленном месте с количеством посетителей 20000 и имеет торговую площадь 1000 кв.м? Каков будет товарооборот магазина, если он находится в относительно оживленном месте с количеством посетителей 20000 и имеет торговую площадь 1000 кв.м?8242,168 млн.руб. 8,243 млн.руб. 6,411 млн.руб. 3,911 млн.руб. все ответы неверны Р Рассмотрите модель зависимости общей величины расходов на питание от располагаемого личного дохода (х) и цены продуктов питания (р): у=а0+а1х+а2р+ 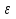 . Определите класс модели и вид переменных модели: . Определите класс модели и вид переменных модели:регрессионная модель с одним уравнением; эндогенная переменная — расходы на питание, экзогенная переменная — располагаемый личный доход, предопределенная переменная — цена продуктов питания модель временного ряда; эндогенная переменная — расходы на питание, лаговые переменные — располагаемый личный доход и цена продуктов питания регрессионная модель с одним уравнением; эндогенная переменная расходы на питание, экзогенные переменные — располагаемый личный доход и цена продуктов питания модель временного ряда; эндогенная переменная — расходы на питание, экзогенные переменные — располагаемый личный доход и цена продуктов питания. Рассчитанный по выборке коэффициент корреляции оказался равным 1. Это означает, что между изучаемыми переменными есть слабая отрицательная линейная связь между изучаемыми переменными есть связь, но она не является линейной между изучаемыми переменными есть функциональная линейная прямая связь между изучаемыми переменными отсутствует связь полученное число никак не интерпретируется Рассчитанный по выборке коэффициент корреляции оказался равным «–1». Это означает, что между изучаемыми переменными есть слабая отрицательная линейная связь между изучаемыми переменными есть связь, но она не является линейной между изучаемыми переменными отсутствует связь между изучаемыми переменными есть функциональная линейная отрицательная связь полученное число никак не интерпретируется Регрессионный анализ заключается в определении: тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи) аналитической формы связи, в которой изменение результативного признака обусловлено влиянием одного или нескольких факторных признаков, а множество всех прочих факторов, также оказывающих влияние на результативный признак, принимается за постоянные и средние значения статистической меры взаимодействия двух случайных переменных степени статистической связи между порядковыми переменными С Связь называется корреляционной: если каждому значению факторного признака соответствует вполне определенное неслучайное значение результативного признака; если каждому значению факторного признака соответствует множество значений результативного признака, т.е. определенное статистическое распределение если каждому значению факторного признака соответствует целое распределение значений результативного признака если каждому значению факторного признака соответствует строго определенное значение факторного признака Системами эконометрических уравнений являются: системы одновременных уравнений системы нормальных уравнений системы рекурсивных уравнений системы независимых уравнений Система одновременных уравнений отличается от других видов эконометрических систем тем, что в ней: одни и те же эндогенные переменные системы в одних уравнениях находятся в левой части, а в других уравнениях — в правой части эндогенная переменная одного уравнения находится в другом уравнении системы в качестве фактора каждая эндогенная переменная является функцией одной и той же совокупности экзогенных переменных Согласно методу наименьших квадратов минимизируется следующее выражение: 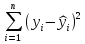 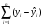 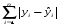 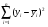 Спецификация модели — это: определение цели исследования и выбор экономических переменных модели проведение статистического анализа модели, оценка качества ее параметров выражение в математической форме выявленных связей и соотношений, установление состава эндогенных и экзогенных переменных сбор необходимой статистической информации С помощью какого критерия оценивается значимость множественных коэффициентов регрессии? хи-квадрат d-критерия t-Стьюдента F – критерия Т Табличное значение критерия Стьюдента зависит И от уровня доверительной вероятности, и от числа факторов, включенных в модель и от длины исходного ряда Только от уровня доверительной вероятности Только от числа факторов, включенных в модель Только от длины исходного ряда Только от уровня доверительной вероятности и длины исходного ряда Табличное значение критерия Стьюдента не зависит от уровня доверительной вероятности от числа факторов в модели от длины исходного ряда от значений коэффициентов регрессии все ответы верны Табличное значение критерия Фишера зависит Только от уровня доверительной вероятности Только от числа факторов, включенных в модель И от уровня доверительной вероятности, и от числа факторов, включенных в модель и от длины исходного ряда Только от длины исходного ряда Только от уровня доверительной вероятности и числа факторов, включенных в модель У Укажите правильную функцию гиперболического тренда: 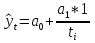 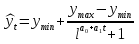 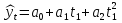 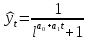 Укажите правильную функцию логарифмического тренда: 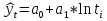 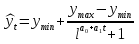 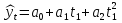 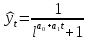 Уравнение гиперболы имеет вид: 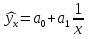 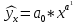 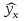 = а0 + а1х + а2х2 = а0 + а1х + а2х2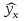 = а0 * = а0 *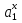 Уравнение множественной регрессии имеет вид: 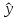 = -27,16 + 1,37х1, -0,29х2. Параметр b1 = 1,37 означает следующее: = -27,16 + 1,37х1, -0,29х2. Параметр b1 = 1,37 означает следующее:при увеличении х1, на одну единицу своего измерения переменная Yувеличится на 1,37 единиц своего измерения при увеличении х1 на 1,37 единиц своего измерения и при фиксированном значении фактора х2, переменная Yувеличится на одну единицу своего измерения при увеличении х1, на одну единицу своего измерения и при фиксированном значении фактора х2, переменная Yувеличится на 1,37 единиц своего измерения при увеличении х1 на 1,37 единиц своего измерения переменная Yувеличится на одну единицу своего измерения Уравнение регрессии имеет вид 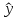 = 2,02 + 0,78х. На сколько = 2,02 + 0,78х. На сколькоединиц своего измерения в среднем изменится 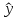 при увеличении х на одну единицу своего измерения: при увеличении х на одну единицу своего измерения:увеличится на 0,78 увеличится на 2,02 увеличится на 2,80 не изменится Уравнение степенной функции имеет вид: 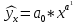 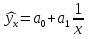 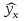 = а0 + а1х + а2х2 = а0 + а1х + а2х2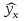 = а0 * = а0 *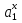 Уравнение Y=+k+(1-)l+u, где Y - темп прироста выпуска, k - темп прироста затрат капитала и l - темп прироста затрат труда, может быть оценено как модель линейной регрессии: непосредственно, с помощью обычного МНК, как зависимость Y от k и l без свободного члена как линейную зависимость (Y-k) от (l-k) со свободным членом непосредственно, с помощью обычного МНК, как зависимость Y от k и l со свободным членом как линейную зависимость (Y-k) от (l-k) без свободного члена невозможно оценить данную зависимость с помощью обычного МНК; требуется нелинейный МНК Ч Частный коэффициент корреляции оценивает: тесноту связи между двумя переменными тесноту связи между тремя переменными тесноту связи между двумя переменными при фиксированном значении остальных факторов тесноту связи между зависимой переменной и всеми факторами, включенными в модель Чему равен коэффициент эластичности, если уравнение регрессии имеет вид 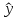 = 2,02 + 0,78x, = 2,02 + 0,78x,  = 5,0; = 5,0; 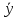 = 6,0: = 6,0:0,66 0,94 1,68 2,42 Что показывает коэффициент регрессии степенной модели? на сколько единиц изменится y, если x изменился на единицу относительную величину изменения y при изменении x на единицу на сколько процентов изменится y, если x изменился на один процент абсолютную величину изменения y при изменении x на единицу Э Экзогенные переменные модели характеризуются тем, что они: датируются предыдущими моментами времени являются независимыми и определяются вне системы являются зависимыми и определяются внутри системы являются лаговыми переменными |
