отчет. А Чтобы найти транспонированную матрицу
 Скачать 22.49 Kb. Скачать 22.49 Kb.
|
|
Вебинар: Матрицы. Действия над матрицами Транспонируем матрицу: А= 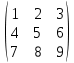 Чтобы найти транспонированную матрицу поменяем строки и столбцы матрицы местами: Чтобы найти транспонированную матрицу поменяем строки и столбцы матрицы местами: = = Возведение матрицы в степень обозначает умножение матрицы на саму себя 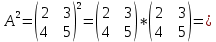 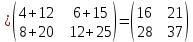 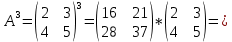 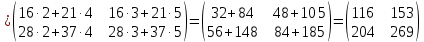 Проверка четвертого свойства транспонирования Транспонированное произведение матриц равно произведению транспонированных матриц, взятых в обратном порядке 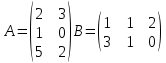 Умножим матрицу А на В: c11 = 2 · 1 + 3 · 3 = 2 + 9 = 11 c12 = 2 · 1 + 3 · 1 = 2 + 3 = 5 c13 = 2 · 2 + 3 · 0 = 4 + 0 = 4 c21 = 1 · 1 + 0 · 3 = 1 + 0 = 1 c22 = 1 · 1 + 0 · 1 = 1 + 0 = 1 c23 = 1 · 2 + 0 · 0 = 2 + 0 = 2 c31 = 5 · 1 + 2 · 3 = 5 + 6 = 11 c32 = 5 · 1 + 2 · 1 = 5 + 2 = 7 c33 = 5 · 2 + 2 · 0 = 10 + 0 = 10 Получим результат: 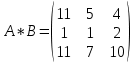 Чтобы найти транспонированную матрицу поменяем ряды и столбцы матрицы местами: Чтобы найти транспонированную матрицу поменяем ряды и столбцы матрицы местами:A*ВT = 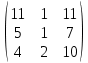 Найдем транспонированную матрицу В: ВT = 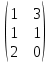 Найдем транспонированную матрицу А: AT = 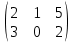 Умножим результат транспортирования матриц B и А c11 = 1 · 2 + 3 · 3 = 2 + 9 = 11 c12 = 1 · 1 + 3 · 0 = 1 + 0 = 1 c13 = 1 · 5 + 3 · 2 = 5 + 6 = 11 c21 = 1 · 2 + 1 · 3 = 2 + 3 = 5 c22 = 1 · 1 + 1 · 0 = 1 + 0 = 1 c23 = 1 · 5 + 1 · 2 = 5 + 2 = 7 c31 = 2 · 2 + 0 · 3 = 4 + 0 = 4 c32 = 2 · 1 + 0 · 0 = 2 + 0 = 2 c33 = 2 · 5 + 0 · 2 = 10 + 0 = 10 В результате получим: AT 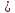 ВT ВT 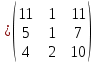 Сравним результаты A*ВT = 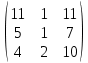 BT BT 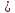 AT AT 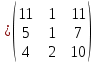 Результат проверки: Данные матрицы равны 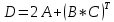 , если 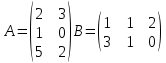 С= С=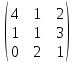 2*А = 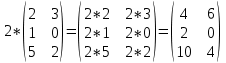 В*С = 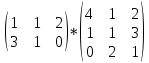 = =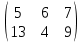 c11 = 1 · 4 + 1 · 1 + 2 · 0 = 4 + 1 + 0 = 5 c12 = 1 · 1 + 1 · 1 + 2 · 2 = 1 + 1 + 4 = 6 c13 = 1 · 2 + 1 · 3 + 2 · 1 = 2 + 3 + 2 = 7 c21 = 3 · 4 + 1 · 1 + 0 · 0 = 12 + 1 + 0 = 13 c22 = 3 · 1 + 1 · 1 + 0 · 2 = 3 + 1 + 0 = 4 c23 = 3 · 2 + 1 · 3 + 0 · 1 = 6 + 3 + 0 = 9 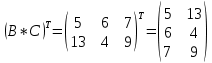 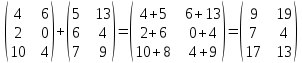 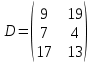 |
