Лекция 3а продолжение 3_НАПРАВЛЯИЩИЕ_СИСТЕМЫ. А электромагнитные волны в направляющих системах понятие о волноводах и объемных резонаторах
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
Глава 4а ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В НАПРАВЛЯЮЩИХ СИСТЕМАХ 1. Понятие о волноводах и объемных резонаторах. Канализация энергии очень высокой частоты по обычным двухпроводным линиям передачи практически невозможна ввиду того, что: 1) провода линии играют роль антенн и, вместо того чтобы передавать энергию потребителю, излучают ее в пространство; 2) активное сопротивление проводов линии при сверхвысоких частотах в силу резко выраженного поверхностного эффекта оказывается настолько большим, что весьма значительная часть энергии затрачивается на нагрев проводов. Применение коаксиального кабеля для канализации энергии весьма высокой частоты экономически также невыгодно. Хотя в этом случае энергия в окружающее пространство и не излучается (так как оболочка кабеля одновременно является и экраном), однако в кабеле велики потери энергии в жиле и диэлектрических шайбах (например из полистирола или полиэтилена), с помощью которых жила крепится внутри кабеля. Коаксиальный кабель применяют для передачи сигналов с диапазоном частот от нуля до нескольких мегагерц и используют в силовых, телефонных и телевизионных устройствах. При частоте больше 109 Гц энергию передают по волноводам. Волновод представляет собой полую трубу прямоугольного или круглого сечения. На рис. 4.1, а изображен прямоугольный волновод. Размеры а и bнаходятся в определенном соотношении с длиной волны. Так, например, при длине волны λ = 10 см берут b- 3,4 см и а = 7,2 см. 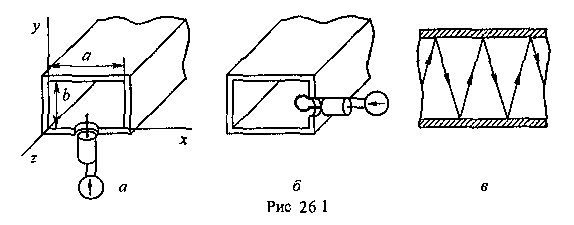 Рисунок 4.1 Энергия внутрь волновода обычно доставляется с помощью неболь шого стерженька, помещенного в волноводе, и коаксиального кабеля, соединенного с генератором высокой частоты (рис. 4.1, а), или с помощью петли с током, помещаемой в волноводе, и коаксиального кабеля, соединенного с генератором высокой частоты (рис. 4.1, б). Иногда волновод возбуждают, соединяя его через щель или диафрагму с другим волноводом или резонатором. Отвод энергии с другого конца волновода: производят с помощью стерженька, петли или через щель» | Энергия передается вдоль волновода, отражаясь от его стенок; (рис. 4.1, в}. Стенки волновода являются как бы направляющими для потока энергии. Небольшая часть энергии проникает в стенки волновода и выделяется в них в виде теплоты. Для уменьшения потерь энергии в стен ках волновода внутреннюю поверхность труб полируют и покрывают: слоем хорошо проводящего металла, например серебра. В качестве резонансных контуров при не очень высоких частотах применяют контуры с сосредоточенными индуктивностями н емкостями, или отрезки линий с распределенными параметрами. При сверхвысоких частотах (при длине волн сантиметрового диапазона) контуры с сосре доточенными параметрами L и С н отрезки линий с распределенными, параметрами оказываются малопригодными, так как они излучают элек тромагнитную энергию и вследствие этого, а также в силу резко выра женного поверхностного эффекта обладают малой добротностью. При сверхвысоких частотах в качестве устройства, выполняющего функции резонансного контура с высокой добротностью, применяют объемные резонаторы. Объемный резонатор представляет собой полый прямоугольный параллелепипед или полый металлический цилиндр с донышками. Стенки резонаторов выполняют из хорошо проводящего материала и полируют. Длины трех ребер прямоугольного резонатора и длина и радиус цилиндрического резонатора находятся, как и в волноводе, в определенных соотношениях с длиной волны и составляют несколько сантиметров. Резонатор возбуждает так же, как и волновод, например, с помощью стерженька или петли с током. В полости объемного резонатора возникают стоячие электромагнитные волны, так как со всех сторон полость ограничена хорошо проводящими стенками. Качественно переход от обычного колебательного контура L, С к пря моугольному объемному резонатору иллюстрируют рис. 4.2, а-г, На рис. 4.2, а изображены две пластины конденсатора, соединенные дву- мя индуктивностями, на рис. 4.2, б индуктивности заменены на две полоски, на рис. 4.2, е - на четыре полоски; на рис. 4.2, г полоски заменены проводящими стенками. При колебательном процессе в резонаторе энергия электрического поля переходит в энергию магнитного поля и обратно. В прямоугольном и цилиндрическом резонаторах энергия каждого из полей распределена по всей полости резонатора. В других устройствах сверхвысоких частот (клистронах, магнетронах) энергии Уэтих полей распределены преимуще- ственно в различных областях. Так, в резонансной полости клистрона (рис. 4.2, е) электрическое поле сосредоточено преимущественно в узком зазоре а (как бы в плоском конденсаторе), а магнитное связано с индуктивностью, роль которой выполняет полость резонатора, примы кающая к узкому зазору. 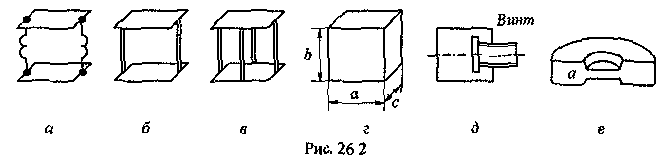 Рисунок 4.2 Под добротностью резонатора понимают Q = ω0Wq/ Р. Здесь Wq- энергия электромагнитного поля, запасенная в резонаторе; Р - активная мощность, затрачиваемая на потери от вихревых токов в стенках резонатора, на потери через щель в виде излучения, а если диэлектрик, имеющийся в полости резонатора, не идеальный, то и на потери в диэ лектрике. Добротность Q достигает значения 104 и более. 2. Типы волн в волноводе. Прямоугольный волновод. Решение для Н волны. Процесс распространения электромагнитных волн в полости прямоугольного волновода будем рассматривать, полагая, что его стенки выполнены из сверхпроводящего материала (γ —» ∞). При этом условии напряженность электрического поля на стенках_волновода будет равна нулю (плотность тока на стенках волновода 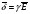 5 = конечна, поэтому при γ —» ∞ Е —» 0). 5 = конечна, поэтому при γ —» ∞ Е —» 0).Полость волновода заполнена диэлектриком, диэлектрическая проницаемость которого εа. Оси координат расположим в соответствии с рис.4.3, а. Размеры полости волновода в направлении оси х обозначим буквой а, а в напраалении оси у - буквой b. Длина волновода в направлении оси z неограничена. Электромагнитное поле в волноводе описывается уравнением: 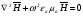 или аналогичным ему уравнением 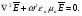 Распространяющиеся в волноводе электромагнитные волны являются волнами, бегущими вдоль оси волновода (оси z) и стоячими в двух остальных направлениях. Стоячие волны в направлении х и у образуются вследствие многократных отражений волн от стенок волновода. 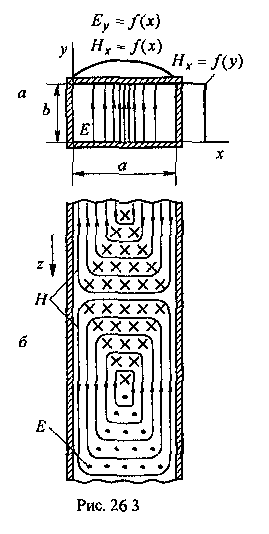 Рисунок 4.3 Тот факт, что волны являются бегущими вдоль оси z, в формально математическом отношении находит свое выражение в том, что при записи каждой из составляющих волн (подобно бегущим волнам в линии с распределенными параметрами) используется множитель 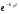 , где kр - коэффициент распространения. , где kр - коэффициент распространения.Волны, распространяющиеся в волноводах, разделяют на два типа: Н - волны и Е-волны. Н-волну называют также поперечно-электрической и обозначают ТЕ; Е-волну - поперечно-магнитной и обозначают ТМ. Кроме волн H и E могут быть еще волны ТЕМ. Они возникают. 9 коаксиальном кабеле (не в волноводе) и полосковой линии. В волне ТЕ1 векторы Е и Н лежат в плоскостях, перпендикулярных направлению распространения волны. Структура Н-волны такова, что составляющую вдоль оси волновод имеет только напряженность магнитного поля, а напряженность элект рического поля расположена в плоскости, перпендикулярной оси волне вода, т. е. для Н-волны: 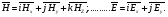 (4.1) (4.1)Для Е волны наблюдается обратная картина: составляющую вдоль оси волновода имеет только напряженность электрического поля, з векторы напряженности магнитного поля расположены в плоскостях, перпендикулярных оси волновода, т. е. для Е-волны. 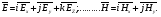 Какой из этих типов волн возникает, зависит от условий возбуждений и геометрических размеров поперечного сечения волновода. Если возбуждение производить с помощью штырька (рисунок 4.1, в), волноводе возникнут Н-волны. При возбуждении с помощью петли с током, расположенной вблизи узкой стенки волновода в соответствии с рисунок 4.1, б, в последнем возникают также Н-волны. Дня Е-волны штырек следует направить вдоль оси z. Приводимые далее выкладки проделаны для Н-волны, но они будут почти такими же и для Е-волны. Если подставить (4.1) в уравнение (4.3), то последнее разобьется натри уравнения для проекций. Для проекции на ось z будем иметь: 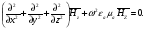 (4.2) (4.2)Воспользуемся методом разделения переменных. С этой целью положим: 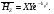 (4.3) (4.3)где Х - функция только х. Y - функция только у. Множитель 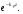 сви- детельствует о том, что вдоль оси z движется бегущая волна. сви- детельствует о том, что вдоль оси z движется бегущая волна.Подставим (4.3) в (4.2): 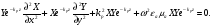 (4.3a) (4.3a)Обозначим 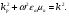 (4.4) (4.4)И разделим (4.3а) на 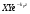 . Получим: . Получим: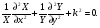 (4.5) (4.5)Сумма двух функций 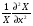 г и г и 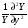 из которых одна является функцией только х, а другая - у, может равняться постоянному числу – k2 только тогда, когда каждая из этих функций есть постоянное число. Перейдем от частных производных к обыкновенным и положим: из которых одна является функцией только х, а другая - у, может равняться постоянному числу – k2 только тогда, когда каждая из этих функций есть постоянное число. Перейдем от частных производных к обыкновенным и положим: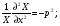 (4.5a) (4.5a)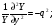 (4.5б) (4.5б)где р и q - некоторые постоянные числа. Решением уравнений (4.5а) и (4.5б) являются функции:  где С1, q и С2, у - постоянные интегрирования, которые найдем из граничных условий. Таким образом, в соответствии с (4.3): 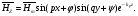 (4.6) (4.6)Здесь комплексная амплитуда Нт = С1С2. Для определения значений р, q, φ, у обратимся к первому и второму уравнениям Максвелла, записанным через проекции напряженностей на оси координат: 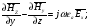 (4.7) (4.7)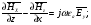 (4.8) (4.8)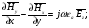 (4.9) (4.9)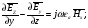 (4.10) (4.10)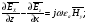 (4.11) (4.11)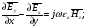 (4.12) (4.12)В силу того, что для H-волны Еz= 0, и поскольку волны являются бегущими вдоль оси г, то 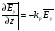 , а , а 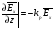 . .Из уравнений (4.10) и (4.11) следует, что:  (4.13) (4.13)Как уже говорилось, на внутренних поверхностях стенок волновода напряженность электрического поля равиа нулю. Следовательно, Ех= 0 при у = 0 и у = b, а Еу = 0 при х = 0 и х = а. Если это учесть, то из уравнений (4.13) имеем 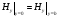 и и 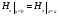 . .Так как 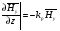 и и  , а Hу = 0 при y = 0 и у = bи , а Hу = 0 при y = 0 и у = bи Нх = 0 при x = 0 и х = а, то из (4.7) и (4.8) следует:  (4.14) (4.14) (4.15) (4.15)Уравнения (4.14), (4.15) служат для определения значений р, q, φ, ᴪ. Подставив (4.6) в (4.14), найдем ᴪ = π/2, q = nπ/b. Из (4.15) определим φ = π/2 и р = тπ/а, где m и n - целые числа; т равно числу полуволн электромагнитной волны, которое разместится по ширине волновода; п показывает, сколько полуволн разместится по высоте волновода. Таким образом:  (4.16) (4.16)Найдем теперь 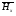 , , 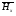 , и , и 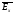 , , 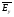 . Для определения . Для определения 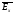 в уравнении-(4.7) в уравнении-(4.7) 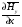 заменим на заменим на 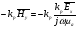 : :Тогда 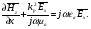 Отсюда: 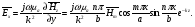 (4.17) (4.17)где 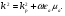 Аналогично: 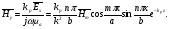 (4.18) (4.18)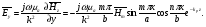 (4.19) (4.19)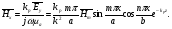 (4.20) (4.20)Проанализируем полученные результаты. Коэффициент kр играет роль постоянной распространения электромагнитной волны вдоль оси z. Если kр будет действительным числом, то волна при своем продвижении по волноводу будет затухать. Затухание будет отсутствовать, если kр - мнимое число. Для того чтобы связать kрс геометрическими размерами волновода а и b c числами т и п, подставим (4.16) в (4.2). Получим: 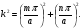 Но 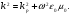 Поэтому 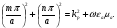 (4.21) (4.21)Отсюда следует, что 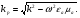 Угловую частоту, при которой kр = 0 называют критической угловой частотой 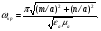 (4.21a) (4.21a)Если 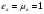 , то , то 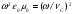 , где vc - скорость света в свободном пространстве. В этом случае kр можно записать так: , где vc - скорость света в свободном пространстве. В этом случае kр можно записать так: 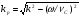 , а , а 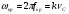 . Ей соответствует частота: . Ей соответствует частота: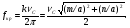 и критическая длина волны  Если угловая частота возбудителя колебаний (тока в стержне или петле рисунок 4.1) 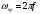 будет больше то будет больше то 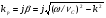 kp оказывается числом мнимым. Поскольку рабочая частота / >/кр, то длина волны в свободном пространстве kp оказывается числом мнимым. Поскольку рабочая частота / >/кр, то длина волны в свободном пространстве 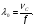 меньше критической длины волны в волноводе меньше критической длины волны в волноводе 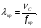 Числа т и n могут принимать целые значения, но не могут равняться нулю одновременно, так как тогда все составляющие E и H отсутствовали бы. Наибольшее значение имеет волна т = 1 и п = 0 (волна H10), для нее по ширине волновода укладывается одна полуволна, а по его высоте интенсивность поля не изменяется. В качестве примера определим ωкр при а = 7,2 см по формуле (4.21а) для волны Н[0. Она равна 13 109 рад/с. Таким образом по волноводу может распространяться энергия лишь весьма высокой частоты. Амплитуда максимальной напряженности электрического поля Етдолжна быть меньше пробивной напряженности поля, иначе произойдет пробой диэлектрика (воздуха, газа или какого-либо другого диэлектрика). При любом способе возбуждения волновода вблизи возбудите может возникать несколько различных типов волн. Для устранения некотором расстоянии от излучателя высших типов волн, размеры а и выбирают так, чтобы для низшего типа волн, например H10, при выбранном значении коэффициента распространения kр являлось мнимым числом, а для ближайшего высшего типа волн, например Н20, kр являлось числом действительным. В зависимости от длины волны размеры а и b берут равными а = (0,7...0,8)λс и b= (0,3.. .0,4) λс Размеры а и b стандартизованы. Под картиной поля в полости волновода понимают совокупность д ний Е и линий Н для выбранного типа поля, Картину поля строят либо в нескольких ортогональных плоскостях ( например, рисунок 4.3, а и 6 или рисунок 4.6, а), либо объемную (например, рисунок 4.6, 6). Сначала целесообразно строить картину поля в плоскости х0у, так как у Н-поля вектор расположен в плоскости х0у и имеет либо только одну, либо две проекции (в зависимости от типа волны), а у Е-поля вектор Н в этой плос- кости имеет тоже либо одну, либо две проекции. В плоскости х0у проекции линий Н и линий Е пересекаются друг с другом под прямым углом (например рис. 4.6, о). Картина поля для волны Н10 изображена рисунке 4.3, а и б. Токи смещения в полости волновода переходят в то проводимости по его стенкам (рисунок 4.4, а). При проводимости стенок волновода, стремящейся к бесконечности, напряженность поля иа стенках волновода стремится к нулю, но плотность тока δ = γЕ конечна, В действительности γ имеет конечное значение (это бдаеп далее учтено при определении потерь в стенках от протекающего по ним тока проводимости). 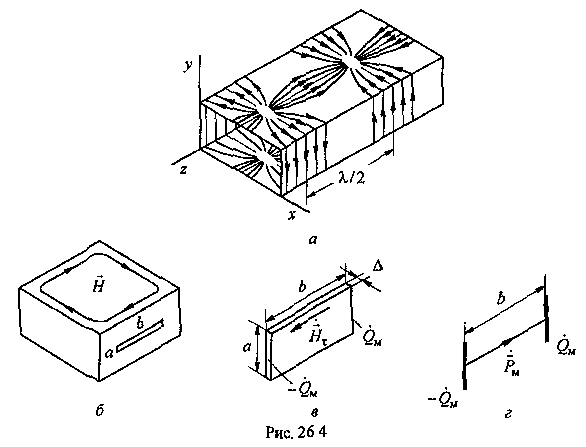 Рисунок 4.4 Для измерительных целей в стенках волновода делают щели (проре- зи), располагая их так, чтобы они не препятствовали протеканию по ним токов проводимости. Щель в стенке волновода используют также для излучения волн из возбужденного волновода в окружающее пространство. Пусть в волноводе возбуждена волна ‘сипа Н10. Поле в волноводе изображено на рис. 4.3.б, эскиз волновода - на рис 4.4, б Воздушная щель размером axb расположена вдоль узкой стенки волновода Отдельно щель изображена на рис 4.4, в Напряженность магнитного поля Н = Нх направлена вдоль шели. Вдоль щели по воздуху проходит магнитный ток смешения: 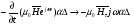 Поверхность, через которую течет магнитный ток смещения, равна произведению аΔ. Этот ток можно рассматривать как производную по времени от магнитного заряда 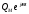 на боковых стенках щели, т е. как на боковых стенках щели, т е. как 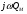 . Отсюда комплексная амплитуда магнитного заряда . Отсюда комплексная амплитуда магнитного заряда 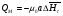 Вс ВсМагнитный момент щели равен 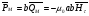 и направлен встречно Нx. Единица измерения РM равна В-c-м. и направлен встречно Нx. Единица измерения РM равна В-c-м.Поле, излучаемое щелью в окружающее пространство, определим как поле магнитного диполя. Так как в воздухе 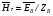 а а 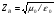 . то . то 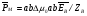 Магнитный момент пропорционален магнитному напряжению на щелн а ЕB, Магнитный момент пропорционален магнитному напряжению на щелн а ЕB, |
