Задания+по+статистике_реш.. Абсолютные и относительные величины
 Скачать 61.45 Kb. Скачать 61.45 Kb.
|
Контрольные задания по теме «Абсолютные и относительные величины»Вариант 7. По промышленному предприятию за отчетный год имеются следующие данные о выпуске продукции:
Определить процент выполнения квартального плана: 1) по выпуску каждого вида продукции; 2) в целом по выпуску всей продукции. Решение
Вывод: Установленный план на 1й квартал по выпуску стали арматурной был выполнен на 99,40%. Перевыполнили план по выпуску проката листового. В итоге процент выполнения плана в целом по продукции так же перевыполнен и составил 101,36% Контрольные задания по теме «Ряды динамики»Вариант 7!!! По статистическим данным по России за 2002 – 2007 гг. вычислить: абсолютные, относительные, средние изменения и их темпы базисным и цепным способами. Рассчитать прогноз на 2008 и 2009 годы.
Решение:  Рис. Динамика показателя за ряд лет Цепные показатели ряда динамики.
В 2007 году по сравнению с 2006 годом производство яиц уменьшилось на 0.1 млрд. шт. или на 0.3%. Максимальный прирост наблюдается в 2005 году (1.1 млрд. шт.). Минимальный прирост зафиксирован в 2004 году (-0.7 млрд. шт.). Темп наращения показывает, что тенденция ряда убывающая, что свидетельствует о замедлении производство яиц. Базисные показатели ряда динамики.
В 2007 году по сравнению с 2002 годом производство яиц увеличилось на 1.5 млрд. шт. или на 4.1%. Сводная таблица.
Расчет средних характеристик рядов. Средний уровень ряда y динамики характеризует типическую величину абсолютных уровней. Для нахождения среднего уровня моментного ряда используют среднюю хронологическую: Среднее значение производство яиц за анализируемый период составило 36.83 млрд. шт. Средний темп роста В среднем за весь период рост анализируемого показателя составил 1.0081 Средний темп прироста В среднем производство яиц ежегодно увеличивалась на 0.8%. Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. Средний абсолютный прирост. С каждым годом производство яиц в среднем увеличивалось на 0.3 млрд. шт. Выполним прогноз на 3 шага вперед, используя показатель среднего темпа роста. y(7) = 37.8*1.0081 = 38.11 y(8) = 38.10618*1.0081 = 38.41 y(9) = 38.414840058*1.0081 = 38.73 Контрольные задания по теме «Индексы» Имеются следующие данные о продажах минимаркетом 3-х видов товаров (A, B и C):
Рассчитать всевозможные индексы. Решение: Индивидуальные индексы. Для расчета индивидуальных индексов цен необходимо цену за 1 ед. каждого вида продукции отчетного периода отнести к цене этой же продукции базисного периода. Это означает, что цена возросла на 2.8% (102.8 – 100). Спад физического объема составил 14.1% (100 – 85.9). ipq=1.028*0.859=0.883 Т.е. стоимость товарооборота снизилась на 11.7% (100 – 88.3). Это означает, что цена снизилась на 4.3% (100 – 95.7). Прирост физического объема составил 12.2% (112.2 – 100). ipq=0.957*1.122=1.074 Т.е. стоимость товарооборота выросла на 7.4% (107.4 - 100). Это означает, что цена возросла на 11.1% (111.1 – 100). Спад физического объема составил 5.6% (100 – 94.4). ipq=1.111*0.944=1.049 Т.е. стоимость товарооборота выросла на 4.9% (104.9 - 100).
а) общий индекс товарооборота ∆Z = ∑q1*p1 - ∑q0*p0 = 58590 - 59040 = 450 За счет влияния всех факторов, общий товарооборот снизился на 0.8% или на 450. б) общий индекс цен (метод Пааше) ∆Zp = ∑q1*p1 - ∑q1*p0 = 58590 - 57763 = 827 За счет изменения цен сводный товарооборот возрос на 1.4% или на 827. в) общий индекс физического объема продукции (индекс Ласпейреса) ∆Zq = ∑q1 · p0 - ∑q0 · p0 = 57763 - 59040 = -1277 За счет изменения объема продаж, товарооборот снизился на 2.2% или на 1277. Покажем взаимосвязь индексов I = Iq · Ip = 0.978 · 1.014 = 0.992 Контрольные задания по теме «Сводка и группировка материалов статистического наблюдения» Вариант 7. Товарооборот и торговая площадь 18 магазинов за отчетный период:
Для выявления зависимости между размером торговой площади и товарооборота магазинов произведите группировку магазинов по торговой площади, разбив совокупность на четыре группы с разными интервалами. В каждой группе и по итогу в целом подсчитайте: число магазинов; объем товарооборота - всего и в среднем на один магазин; размер торговой площади - всего и в среднем на один магазин; Результаты группировки оформите в таблице. Определите эмпирическое корреляционное отношение. Сделайте выводы. Решение: Построим ранжированный ряд исходных данных, построенный по возрастанию признака «Торговая площадь»:
Группировка производится по группировочному признаку. Определим величину (шаг) интервала группировки по формуле: l=  , ,где k – число групп в группировке (по условию k = 4); Xmax – максимальное значение группировочного признака; Xmin - минимальное значение группировочного признака; l – величина (шаг) интервала группировки. l=  = 40; = 40;Определим верхнюю и нижнюю границы для каждой группы:
Составим следующую таблицу, которую введем групповые показатели:
Для расчета средних величин воспользуемся следующей формулой:  . .Для расчета средних показателей по группам преобразуем формулу:  , где j – номер группы. , где j – номер группы.Сведем результаты расчетов в таблицу:
Составим таблицу, иллюстрирующую оборот в среднем на 1 кв.м. торговой площади по группам:
Выводы: По рассчитанным показателям можно заметить следующую закономерность: с ростом торговой площади оборот также увеличивается, однако сокращается оборот на 1 кв.м. торговой площади. Данная закономерность хорошо прослеживается при расчете средних показателей. В первую группу вошли 4 предприятия, характеризующиеся довольно маленькой торговой площадью, среднее значение которой составляет 34 кв.м., где средний оборот – 43,15 тыс. руб. (также саамы маленький среди всех групп). Расчет значений оборота, приходящегося на 1 кв.м. торговой площади по группам, дает информацию о самом большом обороте на 1 кв.м. предприятий, вошедших именно в первую группу среди всех рассматриваемых 18 предприятий. Вторая группа, в которую попали 3 предприятия, характеризуется средней площадью в 92,67 к.м. со средним оборотом 86,9 и с оборотом на 1 кв.м. торговой площади 0,9378 тыс.руб. Третья группа – 9 предприятий со средним оборотом 112,62 тыс.руб. и средней торговой площадью – 115,78 кв.м. и с оборотом на 1 кв.м. торговой площади в 0,9727 тыс.руб. И, наконец, четвертая группа – 2 предприятия со средней торговой площадью – 171,5 кв.м. и средним оборотом – 131,4 тыс. руб. и с оборотом на 1 к.м. торговой площади – 0,7662. По подсчитанным совокупным показателям (всего количество предприятий – 18, совокупный оборот – 1537,1 тыс.руб., совокупная торговая площадь – 1799 кв.м.) можно подсчитать средний оборот по предприятиям, который составил 99,9444 тыс.руб., и среднюю торговую площадь, приходящуюся на одно предприятие 94,9833 кв.м. Контрольные задания по теме «Средние величины» Вариант 7. Продажа товара А на рынках города за два периода:
Определите цену товара А за 1 кг в среднем по городу за каждый период. Дайте обоснование применению формул средних для расчета показателей. Решение: Средняя цена товара А за 1 кг по городу в базисном периоде Средняя арифметическая взвешенная 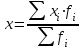
Средняя арифметическая взвешенная рассчитывается по сгруппированным статистическим величинам Х=(15*600+14*400+16*500)/(600+400+500)=22600/1500=15,07 рублей Средняя цена товара А за 1 кг по городу в отчетном периоде Средняя гармоническая применяется, когда исходные данные не содержат частот f по отдельным значениям X, а представлены как их произведение Xf (Xf=w) . Средняя гармоническая взвешенная применяется тогда, когда неизвестны частоты f, а известно w=Xf.  Х=(9500+6800+5800)/(9500/15+6800/14+5800/15)=22100/1506=14,7 рубля | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
