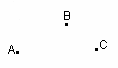Лекция по стереометрии. Лекция 1 Аксиомы стереометрии и их следствия. Аксиомы стереометрии и их следствия
 Скачать 92.96 Kb.
|
|
Дисциплина: математика Тема: Аксиомы стереометрии и их следствия. Тип урока: лекция Цели урока: образовательные: дать определение геометрии как науке и ее подразделам: планиметрии и стереометрии; ознакомить с определением геометрических фигур и рассмотреть основные геометрические фигуры. развивающие: формирование пространственного мышления воспитательные: воспитание чувства прекрасного (умение видеть красоту в повседневном) Ход занятия: Геометрия – это наука, которая изучает свойства геометрических фигур. Геометрическая фигура – это любая совокупность точек. Геометрия подразделяется на планиметрию и на стереометрию, которую мы начинаем изучать. Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве. Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять. Мы начнем изучение стереометрии с основных понятий, основных фигур, аксиом, точно также как это делалось в планиметрии. Основные фигуры в пространстве: точки, прямые и плоскости.
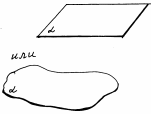
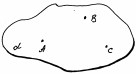
Примеры стереометрических фигур: шар, сфера, конус, цилиндр, параллелепипед и т.д. Плоскость. Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны. На рисунке плоскости изображаются в виде параллелограмма или в виде произвольной области и обозначаются греческими буквами α, β, γ и т.д. 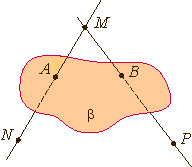 Точки А и В лежат в плоскости β (плоскость β проходит через эти точки), а точки M, N, P не лежат в этой плоскости. Коротко это записывают так: А ∈ β, B ∈ β,  Основные свойства точек, прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах: А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
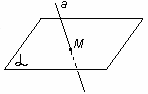
А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости
Замечание. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.
А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. 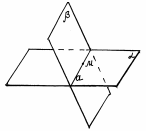    = a и пересекаются по прямой аСледствие 1. Через прямую a и не лежащую на ней точку A проходит плоскость, и притом только одна. 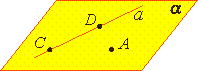 Следствие 2. Через две пересекающиеся прямые a и b проходит плоскость, и притом только одна. 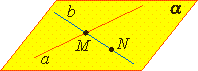 Решение задач Задача 1 Дан тетраэдр АВСD (Рис. 11). Даны следующие точки: точка Е – внутренняя точка ребра АВ, точка Р – внутренняя точка отрезка ЕD, точки М и К, соответственно, на ребрах ВD и DС. 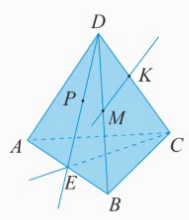 рис. 11. а) В какой плоскости лежит прямая  Ответ:  . Прямая РЕ лежит в плоскости АВD, так как в этой плоскости лежат две точки этой прямой. Точка Е лежит в плоскости АВD и точка Р лежит в этой же плоскости. Значит, по второй аксиоме все точки прямой РЕ лежат в плоскости АВD.б) В какой плоскости лежит прямая  Ответ:  . Прямая MK лежит в плоскости DBC, так как в этой плоскости лежат две точки этой прямой. Точка M лежит в плоскости DBC и точка K лежит в плоскости DBC. По второй аксиоме все точки прямой MK лежат в плоскости DBC.в) В каких плоскостях лежит прямая  Ответ: Прямая BD лежит в плоскости BDА и в плоскости BDС. Значит, прямая BD одновременно лежит в двух плоскостях. Прямая BD есть линия пересечения двух плоскостей. Говорят, что грани АBD,BDС пересекаются по прямой BD. Это можно записать так:  г) В каких гранях лежит прямая  ?Ответ: Прямая АB лежит в грани АВС и в грани АBD. Значит, прямая АВ есть линия пересечения двух этих граней.  д) В каких гранях лежит прямая  ?Ответ: Прямая EC лежит в плоскости АВС и в плоскости ECD, так как точки Е и С лежат одновременно в плоскости АВС и в плоскости ECD. Значит, прямая ЕС есть линия пересечения этих плоскостей.  Задача 2. а) Найдите точку пересечения прямой DК с плоскостью АВС. Решение: Прямая DК содержит точку С. Плоскость АВС содержит точку С. Значит, прямая DК и плоскость АВС пересекаются в точке С. б) Найдите точку пересечения прямой СЕ с плоскостью АDВ. Решение: Точка Е принадлежит и прямой СЕ, и плоскости АDВ. Значит, Прямая СЕ пересекается с плоскостью АDВ в точке Е. Задача 3. а) Найдите точки, лежащие одновременно в плоскостях АDВ и DВС. Решение: Точка В и точка D одновременно лежат и в АDВ, и в DВС. Значит,  . Все точки прямой DВ являются ответом.б) Найдите прямые, по которым пересекаются плоскость АDВ и DВС. Решение: Точка В и точка D одновременно лежат и в АDВ, и в DВС. Значит, прямая DВ есть прямая, по которой пересекаются заданные плоскости. в) Назовите прямые, по которым пересекаются плоскости АDВ и СDА. Решение: Точки А, D лежат в плоскости АDВ, а также точки А, D лежат в другой плоскости СDА. Значит, АD – линия их пересечения:  .г) Назовите прямые, по которым пересекаются плоскости РDС и АВС. Решение: Плоскость РDС совпадает с плоскостью ЕDС. Точка Е и точка С одновременно лежат в двух плоскостях: РDС и АВС. Значит, СЕ – это линия пересечения двух плоскостей.  .Вопросы для самоконтроля: Дать определение геометрии. Дать определение стереометрии Какие основные фигуры в пространстве вы знаете? Как обозначаются основные фигуры в пространстве (точка, прямая, плоскость)? Приведите примеры стереометрических фигур? Какие аксиомы стереометрии и следствия из них вы знаете? Домашнее задание: 1. Перечислите известные вам аксиомы стереометрии. 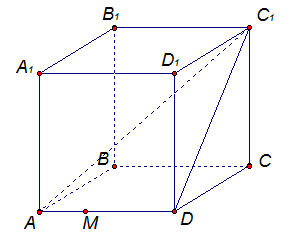 2. Дан куб  .В каких плоскостях лежат прямые: а) AB б) AC1 в) DC 3. Назовите прямые, по которым пересекаются плоскости: а) ABC и ABB1 б) DCC1 и BB1C. |
