Практическая работа по дисциплине «Математика». Математика. Алабина Евгения Игоревна

• Название: Алабина Евгения Игоревна
• Анкор: Практическая работа по дисциплине «Математика»
• Дата: 06.05.2022
• Размер: 272.28 Kb.
• Имя файла: Математика .docx
• Тип: Документы; #515038

Частное профессиональное образовательное учреждение «ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ КОЛЛЕДЖ»

Практическое задание

по	Математике

дисциплине

Выполнил(а) студент(ка)	Алабина Евгения Игоревна
			фамилия имя отчество
Идентификационный номер:		901-0800-150

Пермь 2019

1.Вычислить предел



а) x₀=1

Решение:

Вместо x в числитель и знаменатель подставляем значение 1. Получаем:



б) x₀=2

Решение:

Так как числитель и знаменатель обратились в нуль при x=2, то 2 – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет (x - 2) .

Найдем корни первого многочлена:

3 x² - x - 10 = 0

D=(-1)² - 4·3·(-10)=121



Найдем корни второго многочлена:

- x² +7 x - 10 = 0

D=7² - 4·(-1)·(-10)=9



Получаем: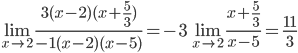


в) x₀=∞

Решение:

 =   = 

2. Найти производные функций:

а)

Решение:

Используем следующие правила дифференцирования

При вычислении были использованы следующие правила дифференцирования:
(x^a)' = ax^a-1

(a)' = 0



(5·x²)' = 5·2·x^2-1(x)' = 10·x

 =   +   +   = 0 +   + 10*x = 


Ответ:


б)

Решение:

Используем следующие правила дифференцирования

При вычислении были использованы следующие правила дифференцирования:
(x^a)' = ax^a-1

(a)' = 0



(cos(x))' = -sin(x)

(sin(x)+1)' = cos(x)

 =   = 

Ответ: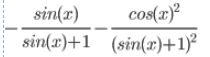

в) y=2^x·cos(x)

Решение:

Используем следующие правила дифференцирования

При вычислении были использованы следующие правила дифференцирования:
(x^a)' = ax^a-1

(a)' = 0



(cos(x))' = -sin(x)

(sin(x)+1)' = cos(x)

Решение ищем по формуле:

(a^f(x))' = a^f(x)*ln(a)*f(x)'

(2^x)' = 2^x·ln(2)(x)' = 2^x·ln(2)

(2^x)' = 2^x·ln(2)

(2^x·cos(x))' = (2^x)'·cos(x)+2^x·(cos(x))' = 2^x·ln(2)·cos(x)+2^x·(-sin(x))

Ответ: -2^x·sin(x)+2^x·ln(2)·cos(x)

г)

Решение:

При вычислении были использованы следующие правила

дифференцирования:
(x^a)' = ax^a-1

(a)' = 0

(f(g(x)))' = f(x)'*g(x)'



(x³)' = 3·x^3-1(x)' = 3·x²


(x³+4)' = 3·x²

 =   =  *3*  = 


Ответ:

3. Исследовать функцию:

y=4x/(x²+16)

Решение:

1) Четность или нечетность функции.


y(-x) = -y(x), нечетная функция

2) Точки пересечения кривой с осями координат.

Пересечение с осью 0Y

x=0, y=0

Пересечение с осью 0X

y=0

x₁=0
3) Исследование на экстремум.

y = 4*x/(x^(2)+16)

Поскольку f(-x)=-f(x), то функция является нечетной.

1. Находим интервалы возрастания и убывания. Первая производная.


или

Находим нули функции. Для этого приравниваем производную к нулю
64-4·x² = 0

Откуда:
x₁ = 4

x₂ = -4

(-∞ ;-4)	(-4; 4)	(4; +∞)
f'(x) < 0	f'(x) > 0	f'(x) < 0
функция убывает	функция возрастает	функция убывает

В окрестности точки x = -4 производная функции меняет знак с (-) на (+). Следовательно, точка x = -4 - точка минимума.

В окрестности точки x = 4 производная функции меняет знак с (+) на (-). Следовательно, точка x = 4 - точка максимума.

2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная.



Находим корни уравнения. Для этого полученную функцию приравняем к нулю.

Откуда точки перегиба:

x₁ = 0

f''(x) < 0	f''(x) > 0	f''(x) < 0	f''(x) > 0
функция выпукла	функция вогнута	функция выпукла	функция вогнута

4) Асимптоты кривой.


Уравнения наклонных асимптот обычно ищут в виде y = kx + b.

По определению асимптоты:


Находим коэффициент k:



Находим коэффициент b:


Получаем уравнение горизонтальной асимптоты:

y = 0

4. Вычислить неопределенные интегралы:

а)

Решение:

Формула интегрирования по частям:


Пусть
U=x
dV=cos(2·x) dx

Тогда:
dU = dx


Поэтому:

Находим интеграл


Ответ:


2.

Решение:

Это табличный интеграл: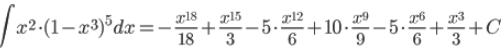



3. ∫ln²(x)dx/x

Решение:

Выражение x подведем под знак дифференциала, т.е.:

x = d(ln(x)), t=ln(x)

Тогда исходный интеграл можно записать так:



Это табличный интеграл:


Чтобы записать окончательный ответ, осталось вместо x подставить ln(x).



5. Вычислить площадь фигуры, ограниченной линиями:

y=x²-4x+3 y=x-1

Решение:

Построим график функций: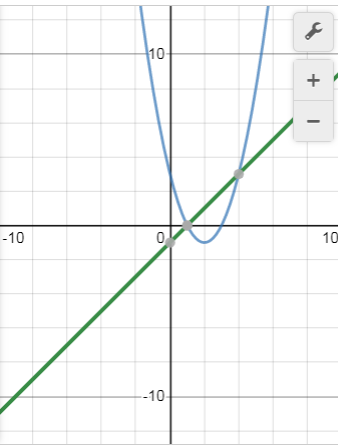



Найдем площадь фигуры:

S=∫ x²-4x+3-(x-1)









Ответ: 4,5