Главная страница
Навигация по странице:

  • Колледж: ГККП «Индустриально-технический колледж, г.Степногорск» Дата

  • Отсутствовали: Тема урока

  • Цели обучения, достигаемые на этом уроке (Ссылка на учебный план)

  • Цель урока все студенты

  • Критерии оценивания Студент достиг цели обучения, если

  • Языковые задачи Языковая цель обучения Студенты будут

  • Лексика и терминология, специфичная для предмета

  • Полезные выражения для диалогов и письма

  • Ход урока Запланированные этапы урока

  • 1. Изучение нового материала

  • Операция нахождения производной называется дифференцированием.

  • Правила дифференцирования

  • Правило деления.

    		•

    апр. План урока Правила дифференцирования. Емн 2 Правила нахождения производной


    Скачать 1.06 Mb.
    НазваниеПлан урока Правила дифференцирования. Емн 2 Правила нахождения производной
    Дата30.11.2020
    Размер1.06 Mb.
    Формат файлаdocx
    Имя файла79c7c5ec-d3d4-4b90-95eb-11113dd21ece.docx
    ТипУрок
    #155238

    Краткосрочный план урока


    7.2. Правила дифференцирования. ЕМН

    7.2.1. Правила нахождения производной

    7.2.2. Производные элементарных функций

    Колледж: ГККП «Индустриально-технический колледж, г.Степногорск»


    Дата:

    ФИО преподавателя: Джункабаева З.А.

    группа:

    Присутствовали:

    Отсутствовали:

    Тема урока
    Определение производной. Правила нахождения производных. Производная степенной функции с действительным показателем

    Цели обучения, достигаемые на этом уроке (Ссылка на учебный план)
    - Находить производную функции по определению;

    - знать и применять правила дифференцирования;

    Цель урока
    все студенты

    - знают таблицу производных элементарных функций;

    - знают правила дифференцирования;
    большинство студентов

    - знают алгоритмы дифференцирования элементарных функций;

    - умеют решать задачи по данной теме;

    некоторые

    - смогут решать задачи повышенной сложности по теме.

    Критерии оценивания
    Студент достиг цели обучения, если:

    - применяет правила дифференцирования суммы и разности

    - применяет правила дифференцирования произведения

    - применяет правила дифференцирования частного

    Языковые задачи
    Языковая цель обучения

    Студенты будут:

    • давать словесную формулировку правил дифференцирования;

    • записывать формулы производной по словесной формулировке;

    • аргументировать выбор способа вычисления дифференциала;

    • использовать правильные математические термины для описания шагов по вычислению дифференциала.


    Лексика и терминология, специфичная для предмета:

    • дифференциал;

    • дифференцировать;

    • правила дифференцирования;

    • Тендер;


    Полезные выражения для диалогов и письма:

    - если я продифференцирую эту функцию, я получу….

    - производная суммы равна ....

    - применим правило дифференцирования суммы…

    - правило вынесения постоянного множителя за знак производной.

    Воспитание ценностей



    Уважение к себе и другим, сотрудничество – через работу в паре, в группе,

    академическая честность – при работе индивидуально,

    открытость – учащиеся самостоятельно могут определить цели урока и критерии.


    Ход урока

    Запланированные этапы урока
    Виды упражнений, запланированных на урок:


    Ресурсы

    Начало урока
    Эпиграф к уроку: «…нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира…» Н.И. Лобачевский.
    1. Изучение нового материала






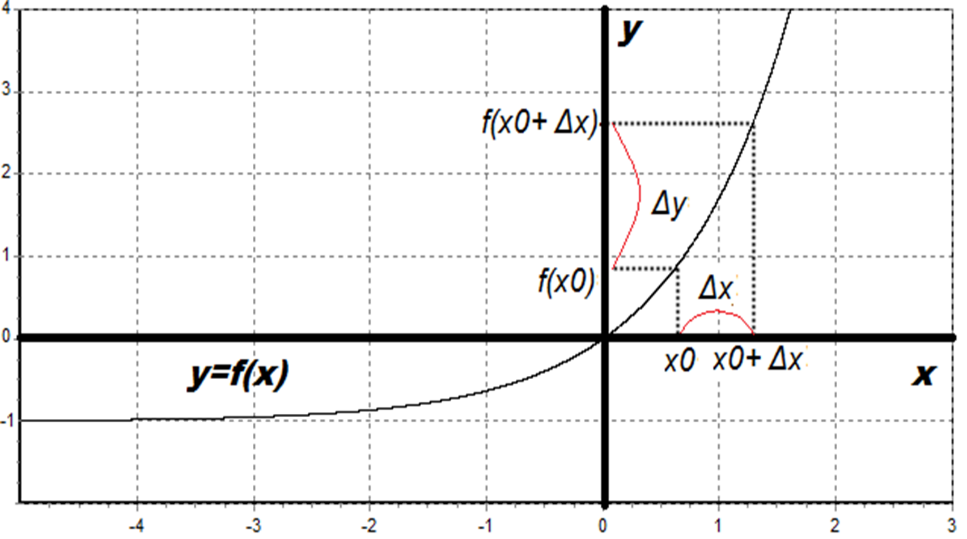
    Определение


    Операция нахождения производной называется дифференцированием.
    Теперь выполните задание по «Обменному курсу».

    Задача по «ПИЗА». ОБМЕННЫЙ КУРС


    Код 1: 12600 ZAR (единицы измерения указывать не требуется)


    Код 1: 975 SGD (единицы измерения указывать не требуется)
    Вопрос 3: Каким способом эта задача связана с нашей темой?

    К чему равняются приращение аргумента и приращение функции?


    Презентация «Определение производной»

    Сборник задач PISA (Programme for International Student Assessment)

    Середина урока
    Если u(х) и v(х) – дифференцируемые функции, то справедливы следующие правила нахождения производных. Для удобства мы запишем эти формулы без указания аргументов.

    Правила дифференцирования

    1) Правило константы. Производная константы равна нулю, т.е.

    C = 0, где С – константа.

    (C u) C u , где С – константа.

    Говорят: «константа выносится за знак производной».
    2) Правило суммы. Производная суммы (разности) равна сумме (разности) производных, т.е.

    (u v) u v
    3) Правило умножения. Производная произведения находится по правилу:

    (u v) u v u v

    4) Правило деления. Производная дроби находится по правилу:

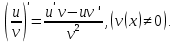
    Производные элементарных функций

    Производные элементарных функций приведены в следующей таблице.



    Задание 1





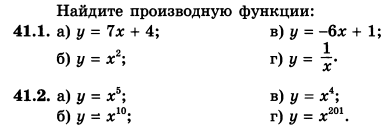
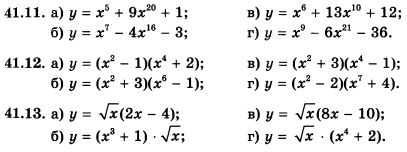
    Дескриптор:

    Студент

    - использует правило дифференцирования суммы;

    - находит производные степенной функции с целым показателем;

    - находит производные степенной функции с рациональным показателем;

    - находит производную функции.

    https://bilimland.kz/ru/subject/algebra/10-klass/pravila-naxozhdeniya-proizvodnyx-proizvodnaya-stepennoj-funkczij?mid=%info%


    Презентация Правила дифференцирования

    Конец урока
    Рефлексия

    В конце урока студенты проводят рефлексию, где возможно студенты могут оценить свою работу и работу своих одногруппников по определенным критериям в начале урока

    - что узнал, чему научился?






    - что осталось непонятным?






    - над чем необходимо работать?












    написать администратору сайта