Алгебра высказываний
 Скачать 43 Kb. Скачать 43 Kb.
|
Под высказывание понимается предложение относительно, которого можно сказать истинно оно или ложно. Высказывание обозначается буквами А,B. ¬ «НЕ», отрицание & «И», конъюнкция v «ИЛИ», дизъюнкция → «ТО» «ВСЕМ», импликация ↔ «т.к.» «т.т.», эквивалентность
Пропозициональная форма принимает значение (И) при возможном распределении при вхождении в нее пропозициональных букв называется тавтологией. Если A → B является тавтологией, то B является логическим следствием А. A → B является тавтологией, то А,B является логически эквивалентными A ↔ B => A<=>B. Предложение 1. А, A → B тавтологии, то В тавтология, т.к. предполагая противное, т.е. при некотором распределении B-Л, то А будучи тавтологией при этом распределении примет значение ИСТИНА, то B-Л, что противоречит условию, т.о. предложение неверно. Предложение 2. Если А тавтология, a1, a2,…,an. B, A1, A2,…An, то B – тавтология. A - ¬ a1 → (a1→a2) B - ¬ (a2 & a3) → (a2 & a3) → (a1 v ¬ a2) A1 A2 A3 Постановка приводит к тавтологии, т.к. если при некотором распределении А, примет значения ИСТИНЫ, то в силу построения B примет значение ИСТИНА, что и А, если вместо А1, А2, А3 поставить х1, х2, х3, т.е. значения ИСТИНА ч.т.д. Предложение 3. Если пропозициональную форму А при помощи замены А1, В1, В, то (A1 ↔ B1) → (A ↔ B) тавтология. Основные равносильности (законы) алгебры высказываний.
Предложение 4. Всякую истинностную функцию можно определить при помощи пропозициональной формы. Следствие 1. Всякую истинностную функцию, можно определить при помощи пропозициональной формы содержащую одну и следующих трех пар связей: ¬, &; ¬,v; ¬,→. Доказательство: ¬, & в силу предложения 4 получается при помощи равносильности 15; ¬,v следует из равносильности 14; ¬,→ следует из равносильности 16,17. Следствие 2. Любую истинностную функцию можно определить при помощи пропозициональной формы содержащую связку Шефера (|) определяется следующим образом
Стрелки Пирса (  ) )
Док-во: достаточность Шефера следует из того, что
A&B – (A|A)|(B|B) Достаточность Пирса:
AvB – (A  A) A) (B (B B) B)Докажем единственность, для того рассмотрим h(A,B), которая будет определять любую истинностную функцию h(И,И) = Л h(Л,Л) = И
¬ недостаточно для выражения всех истинностных функций таких как при помощи отрицания не может быть выражена тождественность функций, что и доказывается следствие 2.
Формальные теории теоремы теории L определяются, если выполняется 4 условия:
Г 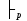 А из множества формул Г выводится формула А, в теории р, если существует конечная последовательность формул А1,А2,..,Аn, которая заканчивается формулой А и i= А из множества формул Г выводится формула А, в теории р, если существует конечная последовательность формул А1,А2,..,Аn, которая заканчивается формулой А и i=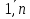 , Ai является: , Ai является:
|) L, A,B,C,…, ¬, →, (,). ||) Опр. понятие формулы теории L, является пропозициональной формой, которая содержит 2 связки ¬, →. Заметим, что другие связки будем использовать для сокращения записи формы и оставим в силу соглашение об экономии скобок. |||) A,B,C следующие формулы являются аксиомами теории L. (А1) А→(B→A) (A2) (A→(B→C) →((A→B) →(A→C)) (A3) (¬B→¬A) →((¬B→A) →B) |V) Единственным правилом вывода является правило Модус Понус (MP).
/\ 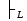 A→A A→AДок-во:
1-5, 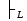 A→A (из пустого множества в теории Lвыводима A влечет А) A→A (из пустого множества в теории Lвыводима A влечет А)Теорема Дедукции теории L. Если Г, А 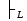 B => Г B => Г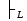 A→B A→BСледствие 1. A→B, B→C 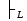 A→C. Док-во: A→B, B→C, A A→C. Док-во: A→B, B→C, A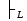 C. C.Следствие 2. A→( B→C),B 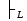 A→C. Док-во: A→( B→C),B,A A→C. Док-во: A→( B→C),B,A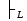 C. C.Следствие 3. A→( B→C) 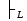 B→(A→C). Док-во: A→( B→C),B B→(A→C). Док-во: A→( B→C),B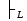 (A→C). (A→C).
Теорема 1. Всякая теорема теории L является тавтологией 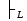 A => AT. A => AT.Док-во: теорема получается из аксиом (А1) (А2) (А3), которые являются тавтологиями (А1) А→(B→A) И Л И Л Л (A2) (A→(B→C) →((A→B) →(A→C)) И И Л Л Л Л И И Л Л И Л Л (A3) (¬B→¬A) →((¬B→A) →B) ИЛИЛИ Л ИЛИИ Л Л Теорема 2. Всякая тавтология является теоремой теории L. Теория L непротиворечива (n/n), т.к. если предположить противное. Теория L называется разрешимой, если существует алгоритм распознания формулы на теорему. Теорема. Теория L является разрешимой. 1948 г. Парский построил алгоритм, для любой формулы определяющий является ли формула теоремой.
Аксиома называется независимой подмножеству Х, если не может быть выделена из Х при помощи правила вывода. Х,Х если каждая аксиома из Х независима от Х, то Х,У – независимы. Теорема. Множество аксиом (А1) (А2) (А3) независимы. Док-во: рассмотрим 3-х значную логику 0,1,2 в которой
Называется, выделенной покажем, что
Формула принимающая только значение 0 называется гратеской. (A→(B→C) →((A→B) →(A→C)) (А2) 1 0 1 2 0 2 1 2 1 2 1 2 0 0 0 2 0 1 2 0 2 2 2 0 2 1 1 0 2 2 1 2 1 2 2 2 1 2 1 (¬B→¬A) →((¬B→A) →B) (А3) 1 1 0 0 2 2 1 1 0 2 2 1 0 2 0 1 0 2 0 2 0 0 2 2 MP: при помощи импликации MP сохраняет выделенность. (А1) А→(B→A) 1 2 2 0 1
1939 г. создана машина Тьюринга. Потенциальная бесконечная лента разбита на множество ячеек, каждый из которых записан символ а, т.е. записывается некоторое слово w. При необходимости слева или справа, может быть добавлена новая ячейка, которая записана пустым символом. 3 команды:
Множество команд называется программной машины Тьюринга. 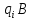 – машина находится в состоянии – машина находится в состоянии 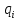 словом B называется конфигурацией. словом B называется конфигурацией.Если машина Тьюринга преобразует аргументы, некоторой функции изначально стандартной конфигурации, то она вычисляет функцию, которая вычислима по Тьюрингу. Тезис Тьюринга гласит, что функция вычислима, т.е. существует алгоритм вычисления ее значения <=> вычислима по Тьюрингу тем самым получаются точные понятия алгоритма при помощи машины Тьюринга.
Терм это:
Формула:
Терма t называется свободной, если формула не содержит связанных вхождений. Терм Xi является свободным термом для переменной Xi в любой формуле.
Интерпретация – это непустое множество D – область интерпретации и состоящее 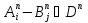 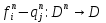 Предметная константа ai, Di, Xi, D. Например:
Если формула выполнима на любой последовательности, если не выполнима на любой последовательности, на любой интерпретации, то называется ложной. Если формула истина в любой интерпретации, то она логически общезначима. Если в некоторой интерпретации истины все аксиомы, то эта интерпретация называется моделями данной теории. Свойства выполнимости истинности:
¬A – Л <=> A – И
AvB – выполнима на 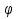 <=> А выполнима и В выполнима на <=> А выполнима и В выполнима на 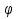 . .A→B выполнима на 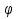 <=> А выполнима и В выполнима на <=> А выполнима и В выполнима на 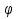 , или А не выполнима и В не выполнима на , или А не выполнима и В не выполнима на 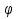 . .
Тавтология является теоремой и получается из аксиом (А1) (А2) (А3), которые являются логически общезначимыми, при помощи MP, которая в силу свойства |V сохраняет истинность формул.
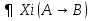 выполнима на выполнима на 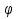 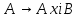 не выполнима на не выполнима на 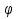 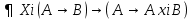 не выполнима на не выполнима на 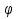 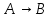 выполнима на выполнима на 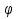 | | 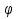 (xi) = (xi) = 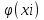 (*) (*)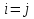 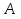 выполнима на выполнима на 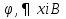 не выполнима на не выполнима на 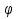 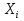 не является свободной переменной V|||, не является свободной переменной V|||, 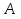 выполнима на выполнима на 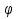 , т.о. , т.о. 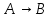 невыполнима на невыполнима на 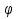 (**) (**)Т.к. * и ** противоречие, предположение неверно. Формула 11 является логически общезначимой.
Логические аксиомы теории первого порядка K (А1) А→(B→A) (A2) (A→(B→C) →((A→B) →(A→C)) (A3) (¬B→¬A) →((¬B→A) →B) (А4) 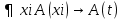 , t свободный терм xi в A(xi) , t свободный терм xi в A(xi)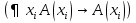 (A5) 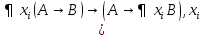 не свободная переменная А не свободная переменная АПО (правило обобщения) : 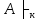 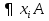
Теорема 1. Всякий частный случай тавтологии является теоремой теории первого порядка. Док-во: ]W полученная из тавтологии Т, тогда по теореме о полноте теории L. T – является теоремой теории L, т.е. имеется вывод из пустого множества формулы Т. Преобразуем этот вывод следующим образом:
T: ¬A1 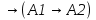 W: 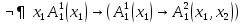 Теорема 2. Исчисления предикатов является непротиворечивой теорией.
|

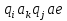 - машина находится в состоянии
- машина находится в состоянии 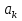 (заменяет
(заменяет 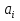 ).
).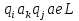 - сдвиг ячейки влево.
- сдвиг ячейки влево.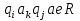 - сдвиг ячейки вправо.
- сдвиг ячейки вправо.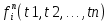
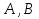 формула => A→B формула
формула => A→B формула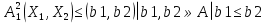
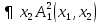
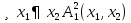
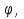 В не выполнима на
В не выполнима на 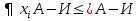
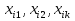 , то формула А на последовательности
, то формула А на последовательности 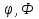 ведет себя одинаково, т.к. выполнимость формул на последовательности интуитивно можно понимать как
ведет себя одинаково, т.к. выполнимость формул на последовательности интуитивно можно понимать как 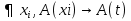 ,при этому получается
,при этому получается 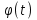 вместо Xi возможно, т.к. по условия t - свободный терм и поэтому его переменные не могут оказываться связанными, т.о. формула является логически общезначимой.
вместо Xi возможно, т.к. по условия t - свободный терм и поэтому его переменные не могут оказываться связанными, т.о. формула является логически общезначимой.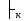 W
W