Алгоритмизации

• Название: Алгоритмизации
• Дата: 27.09.2022
• Размер: 1.15 Mb.
• Имя файла: 12_100229_1_124427 (1).docx
• Тип: Документы; #700459
• страница: 12 из 67

ЗАДАНИЕ 2. Разветвляющиеся алгоритмы

Первыйуровеньсложности

Составить программу нахождения требуемого значения с исходными данными x, y, z. Обозначение: min иmax– нахождение минимального и максимального из перечисленных в скобках значений элементов.

_{1. m;=} max ( x, y, z) _{+ 5}

2. 
   _n= min ( x
   

y, yz)

;
min ( x, y) max ( x, y)

xy<sub>3.

p</sub>y|zmin ( ,

) − max (

, ) |

max ( x

y+ z, x

yz)

= ; 4. q= ;

2 min ( xyz, +x�y+�z)

_{5. r}xmyaxz[ min ( , ) , ]

min [max ( x, y), max ( y, z) ]

=; 6.

3

s= ;

max ( y, z)

xmaxy[min ( ,5), max ( , 0)]

7. t= ; 8. v

5

max[min( x

y, y− x), 0 ] ;

9. 
   w+�m=ax² [max( x
   

y, x

y), 0 ] ; 10.

_z= min (0, x) − min ( 0, y)

;


;
max ² ( y, x)

11. u=

min ( y, z)
; 12.

_q= min ( x+ y z, xyz)

max[min ( x, y), min ( y, z)]

min ( xy z, x�y+/−z)

13. q=

max ( x

y+ z, xyz)
; 14. u=

max ( y, z) _;

max[ x

yz, x/(+y�z+)]

min[min ( x, y), min ( y, z)]

15. u=

min ( y, z ) _. max[max ( x, y), max ( y, z)]

Второйуровеньсложности

Вычислить значение y в зависимости от выбранной функции �(x), аргумент которой определяется из поставленного условия. Возможные значения функции �(x): 2x, x ², х/3. Предусмотреть вывод сообщений, показывающих, при каком условии и с какой функцией производились вычисления у.

ax1.

=xln(1

1/ 5 ₎

cos²[

+( ) +�1]+, где

^□ z² ;

x=_�

z< 1;

_�z1;

z≥+1.

2. y,= ^2a

( x) +�bcos

| x|
где

_{x= �}2 + z;

z<1;

x² + 5

�


2
_�sin z;

z≥ 1.

+ xa

2. 
   xb
   

(x)
cos^{2 3}
sin^3
2 , где

x=^�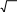


�
�

z;

z³ ;

z< 1;

z≥ 1.

2. 
   y
   

2acos³
x=²
sin ² x³
−+b�(x) , где

^�z³ + 0,2;

x=_�

z<1;

2. 
   y
   

a(x)

ln(x

2,5�)

=b+(−e^x−+e^−x) , где

_�z

x=^�

ln z;

z/ 3; z

z≥+1.

−1<;−

�
^□ | z|;

z≥ −1.

−= 6.

y� ² asin ² x

^3bcos²
(x) , где

_x=� z;

z< 0;

�
3 4 _�^{sin z;}

z≥ 0.

3 2 2

_�z2

z; z<−0;

7+.�=y+ sin [c

(x) d

x], где

x=_�

�

z³;

z≥ 0.

xa8. x
csinx² ( )
cos^{5 3}
ln ^2/5 , где

_x=� 2z1;

z≥+0;

�

2
_�ln( zz);

z<−0.

b�(x)

^�z² / 2;

z≤ 0;

9. y+=,

cos x

aln tg

2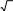

где

x=<sub>�

□</sub> z;

z> 0.

d(x)e^sin 3 ^x+�cln( x+1)

^�z² +1;

z< 1;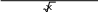

�
10.

y= , где

^x=�z−1;

z≥ 1;

11.

2,5a�e^−3x− 4bx²

y=
, где

_□ 1

x=^{� 2}

; z> 0;

ln | x| �(+x)

�z+ 2z

_□ 1 − z³;

z≤ 0.

12. 
    y
    

asin³[
(x)²�=1] +−cln | x| +e^x
, где

_x=^� z1;

z≤+1;

�

2
_�1/ z1;

z>−1.

12. 
    y
    

sin[
( )]
cos kxln
, где

_x=� z;


□ _2
�z1;

z>1;

z≤+1.

+�14=.
y+ bcos[a
(x)]

sin ^x

5

ae^x, где

_x=^� z;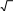


�
_�3z1;

z> 0;

z≤+0.

15. y

2. 
   (x)[asin x
   

d�e+⁽�^+x−=³⁾ ], где

_x=� 3z;

z>−0;

�
^□ z²;

z≤ 0.