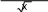ЗАДАНИЕ 3. Циклические алгоритмы
Первыйуровеньсложности
Составить программу для определения таблицы значений функции у в произвольном диапазоне [a, b] изменения аргумента хс произвольным шагом
h. Значения a, b, h вводятся с клавиатуры. Таблица должна содержать следующие столбцы: порядковый номер, значение аргумента x, значение функции, сообщение о возрастании или убывании функции.
Определить максимальное и минимальное значения функции.
1. Y(x) =
2. Y−(x=)
2 sin x
(1 − x)2
, a = –π; b = π; h = 0,4.
x
ln a2s=in0,7,; b= 1,8; h= 0,1.
2
xsin( )
3. Y(x) = a= –0,54; b= 2,,5; h= 0,2.
1 − 2xcos π+ x2
4
x2
−= 4.a= –Y0−,(9x;)b=(12,7; h)=co0s,3x.
4
xsin x, 2
xcos − x2
5. Y(x) = a4= –2; b=, 0,8; h= 0,2.
1 − 2xcos π + x2
4
x2 xx
 =6. a−=+Y–�(1x,9); b( =6. a−=+Y–�(1x,9); b(= 2,7; h=3)0,е3.2 ,
Yx x7.
4 ( ) =x 2
2
15 10+sin(
π)+,
a= –0,4π; b= 0,4π; h= 0,5.
8. (Yxе)x=
xsin ,
a= –0,3π; b= 1,3π; h= π/10.
9. Y=(x)
x2 cos xsin x,
a= –π/2; b= π/2; h= π/10.
Y10x.
x(−)=x
log(
0,6 ),
a= –3; b = 3; h = 0,5.
11x.
Y−(x=) хπ; sbin= π, ; h= π/6.
12. ac=os– 2 ( ) Yеxxa= =–10 ,9е+;2bx=−+21,, h= 0,3.
x2
−= 13a. = –Y0−,(9x;)b=(12,7; h)=co0s,3x.
4
xsin x, 2
14.
Y(x) =
1
2
a= –0,1,; b= 2; h= 0,1.
1
15.
Y=( x)
sin
xcos x,
a = π; b= 2π; h = π/15.
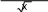 Второйуровеньсложности Второйуровеньсложности Значение аргумента xизменяется от aдо bс шагом h. Для каждого x найти значения функции Y( x), суммы S( x) и | Y( x)– S( x)| и вывести в виде таблицы. Значения a, b, hи nвводятся с клавиатуры. Так как значение S( x) является рядом разложения функции Y( x), значения S и Y для заданного аргумента x должны совпадать в целой части и в первых двух-четырех позициях после десятичной точки. Работу программы проверить для a= 0,1; b= 1,0; h= 0,1; значение параметра n выбрать в зависимости от задания.
S(x)
n∑(−1=)kk=0x2 k+1, (2 k+1)!Y( ) =.sin( )
S(x)
n∑ k=1(−1=)k+1 sin(kx),kkY=(x. ) x2
ncos( )
xcos π
3. S(x) = ∑ 4xk,
Y(x) e
4 cos(xsin(π=/ 4)) .
k=0 k!
4. S(x)
n
∑(−1=)k
x2k
,
Y( )
cos( ) .
k=0
n
5. S(x) = ∑
k=0
(2k)!
cos(kx),
k!
Y(x) = ecos xcos(sin(x)) .
6. S(x) =
n2k+1 2k
=. Y+(x)
2
(1 2x2x)e
∑ x,
k=0 k!
n7. S( x) = ∑k=1xkcos k 3 ,kY+(x)1 −=.ln(1 2 3 x2 )
S(x)
n∑ k=1(−1=),kcos(kx)k21 ( ) Y. x(4 2 −=πx2 / 3)
n
k+1
x2k+1
1 + x2
S(x)
∑ (−1=)k=14 k2 −1 ,Y−(x) =.2 arctg(x)x/ 2
k=0
nx2kex+ e− x
S( x) = ∑ (2k)! ,Y( x) =.2
n
1(1./ S2)(x) =,∑
k=0
k2 +1
k
x=
k!
+ Y+(x)
(x2 / 4
x/ 2
1)e
x/ 2 .
nk2k2 +1 2kx2 x
12.
S(x)
∑(−1=)
k=0
n
k
−x= ,
(2k)!
(2x)2k
Y−(x) (1
) cos(x)
2
2
sin( x) .
2
13.
S(x)
∑(−1=)
k=1
,
(2k)!
( )Y
2x(cos
−=1)x.
k=0
nx2k+1 ex− e− x
14.
S(x) = ∑ (2k+1)! ,
Y(x) =.
2
n
k+1
x2k
15.
S(x)
∑Y(−+1=x−)= . xarctgx
(x)
( ) ln
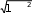 k=1 k=12 k(2 k−1) |
 Скачать 1.15 Mb.
Скачать 1.15 Mb. =6. a−=+Y–�(1x,9); b(
=6. a−=+Y–�(1x,9); b( ( ) Yеxxa= =–10,9е+;2bx=−+21,, h= 0,3.
( ) Yеxxa= =–10,9е+;2bx=−+21,, h= 0,3.