ФИЗИКА ЗАЧЕТНЫЕ ВОПРОСЫ. Аналитический в виде уравнения или формулы у f(х)

• Название: Аналитический в виде уравнения или формулы у f(х)
• Анкор: ФИЗИКА ЗАЧЕТНЫЕ ВОПРОСЫ .doc
• Дата: 04.03.2017
• Размер: 1.28 Mb.
• Имя файла: ФИЗИКА ЗАЧЕТНЫЕ ВОПРОСЫ .doc
• Тип: Документы; #3378
• страница: 2 из 7

две свои составляющие части — корреляционный анализ и регрессионный анализ. Корреляционный анализ — это количественный метод определения тесноты и направления взаимосвязи между выборочными переменными величинами. Регрессионный анализ — это количественный метод определения вида математической функции в причинно-следственной зависимости между переменными величинами. Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными. Корреляционный анализ тесно связан с регрессионным анализом (также часто встречается термин «корреляционно-регрессионный анализ», который является более общим статистическим понятием), с его помощью определяют необходимость включения тех или иных факторов в уравнение множественной регрессии, а также оценивают полученное уравнение регрессии на соответствие выявленным связям (используя коэффициент детерминации)

Вопрос 26

Линейный коэффициент корреляции Для устранения недостатка ковариации был введён линейный коэффициент корреляции (или коэффициент корреляции Пирсона), который разработали Карл Пирсон, Фрэнсис Эджуорт и Рафаэль Уэлдон (англ.)русск. в 90-х годах XIX века. Коэффициент корреляции рассчитывается по формуле^[10][8]: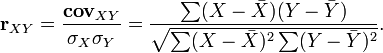



где ,  — среднее значение выборок.

Коэффициент корреляции изменяется в пределах от минус единицы до плюс единицы^[11].

ДоказательствоЛинейный коэффициент корреляции связан с коэффициентом регрессии в виде следующей зависимости: где — коэффициент регрессии, — среднеквадратическое отклонение соответствующего факторного признака^[12].Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определенного символа. Такой график называется «диаграммой рассеяния». Свойства коэффициента корреляцииНеравенство Коши — Буняковского:если принять в качестве скалярного произведения двух случайных величин ковариацию , то норма случайной величины будет равна , и следствием неравенства Коши — Буняковского будет:Коэффициент корреляции равен тогда и только тогда, когда X и Y линейно зависимы (исключая события нулевой вероятности, когда несколько точек «выбиваются» из прямой, отражающей линейную зависимость случайных величин):где . Более того в этом случае знаки и k совпадают:Если X,Y независимые случайные величины, то . Обратное в общем случае неверно.

Вопрос 27

Физика — это наука о природе в самом общем смысле (часть природоведения). Она изучает вещество (материю) и энергию, а также фундаментальные взаимодействия природы, управляющие движением материи.Некоторые закономерности являются общими для всех материальных систем, например, сохранение энергии, — называют физическими законами. Физику иногда называют «фундаментальной наукой», поскольку другие естественные науки (биология, геология, химия и др.) описывают только некоторый класс материальных систем, подчиняющихся законам физики. Например, химия изучает атомы, образованные из них вещества и превращения одного вещества в другое. Химические же свойства вещества однозначно определяются физическими свойствами атомов и молекул, описываемыми в таких разделах физики, как термодинамика, электромагнетизм и квантовая физика.Физика тесно связана с математикой: математика предоставляет аппарат, с помощью которого физические законы могут быть совершенно точно сформулированы. Физические теории почти всегда формулируются в виде математических выражений, причём используются более сложные разделы математики, чем обычно в других науках. И наоборот, развитие многих областей математики стимулировалось потребностями физических теори

Вопрос 28

Физика и другие естественные науки. Тесная связь Ф. с др. отраслями естествознания привела к тому, что Ф. глубочайшими корнями вросла в астрономию, геологию, химию, биологию и др. естеств. науки. Образовался ряд пограничных дисциплин: астрофизика, геофизика, хим. физика, биофизика, молекулярная биология и др. физика всегда оказывала и продолжает оказывать огромное влияние на все развитие науки. Физика - это основная область естествознания, наука о свойствах и строении материи, о формах ее движения и изменения, об общих закономерностях явлений Природы.

Физ. методы исследования получили решающее значение для всех естеств. наук. Электронный и туннельный микроскопы на неск. порядков превысили границы оптич. методов исследований и дали возможность наблюдать отд. атомы и молекулы. С помощью рентг. структурного анализа изучена и продолжает изучаться структура сложнейших биол. молекул и живых тканей. Революция в биологии, связанная с возникновением молекулярной биологией и генетики, была бы невозможна без Ф.

Искусств, радиоакт. изотопы («меченые атомы») сыграли неоценимую роль для исследования обмена веществ в живых организмах. Mн. проблемы биологии, физиологии и медицины были решены с их помощью. Законы квантовой механики лежат в основе теории хим. связи. С помощью физ. методов удаётся осуществить хим. реакции, не идущие в обычных условиях. «Меченые атомы» позволяют проследить кинетику хим. реакций. Создана методика измерения скорости протекания быстрых хим. реакций с помощью пучков мюонов, полученных на ускорителях. Для решения некоторыхрых физ--хим. вопросов используют структурные аналоги атома водорода - позитроний и мюонмий, свойства которых были установлены физиками.

Идеи ядерной Ф. становятся неотъемлемой частью геол. концепций. С их помощью, в частности, измеряют возраст минералов Земли.

На современном этапе развития астрономия и физика так сильно переплетаются, а их влияние друг на друга так огромно, что порой трудно отличить, где кончается астрономия и начинается физика. Развитие физ. электроники позволило наблюдать процессы, протекающие в миллиардные доли секунды, привело к революции в астрономии-созданию радиоастрономии. Все естественные науки оказывают огромное взаимное влияние друг на друга, они все взаимосвязаны. Так на стыке химии и физики возникла физическая химия, на стыке физики и биологии - биофизика. Геофизика, геохимия, астрофизика,- все это только небольшое число так называемых смежных наук.

Вопрос 29

Физика и биология.

Революцию в биологии обычно связывают с возникновением молекулярной биологии и генетики, изучающих жизненные процессы на молекулярном уровне. Основные средства и методы, используемые молекулярной биологией для обнаружения, выделения и изучения своих объектов (электронные и протонные микроскопы, рентгеноструктурный анализ, электронография, нейтронный анализ, меченые

атомы, ультрацентрифуги и т. п.), заимствованы у физики. Не располагая этими средствами, родившимися в физических лабораториях, биологи не сумели бы осуществить прорыв на качественно новый уровень исследования процессов, протекающих в живых организмах.

С физикой тесно связана и химия. Чем больше усложнялись химические исследования, тем больше аппаратура и методы расчетов физики проникали в химию. Необходимость измерения тепловых эффектов реакции, развитие спектрального и рентгеноструктурного анализа, изучение изотопов и радиоактивных химических элементов, кристаллических решеток вещества, молекулярных структур потребовали создания и привели к использованию сложнейших физических приборов эспектроскопов, масс-спектрографов, дифракционных решеток, электронных микроскопов и т.д. С возникновением теории относительности, квантовой механики и учения об элементарных частицах раскрылись еще более глубокие связи между физикой и химией. Оказалось, что разгадка объяснения существа свойств химических соединений, самого механизма превращения веществ лежит в строении атомов, в квантово-механических процессах его элементарных частиц и особенно электронов внешней оболочки. Именно новейшая физика сумела решить такие вопросы химии, как природа химической связи, особенности химического строения молекул органических и неорганических соединений и т.д. Еще одним свидетельством плодотворности влияния физики на химическую науку является все расширяющееся применение физических методов в химических исследованиях. Поразительный прогресс в этой области особенно отчетливо виден на примере спектроскопических методов. Открытие физиками явления магнитного резонансного поглощения привело к появлению спектроскопии ядерного магнитного резонанса, наиболее информативного современного аналитического метода и метода изучения электронного строения молекул, и спектроскопии электронного парамагнитного резонанса, уникального метода изучения нестабильных промежуточных частиц - свободных радикалов, появились лазеры.

Вопрос 30

Гармонические колебательные движения. Ур-е гармонического колебания. Условия невозможности колебательного движения.

Повторяющиеся движения или изменения состояния называют колебаниями. Всем колебаниям независимо от их природы присущи некоторые общие закономерности. Колебания распространяются в среде в виде волн. Среди различных видов колебаний наиболее простой формой является гармоническое колебание, т.е. такое, при котором колеблющаяся величина изм-ся в зависимости от времени по закону sin или cos. Гармонические колебания совершают: 1)пружинный маятник(изм-ие упругой силы, согласно закону Гука, пропорц-но изм-ю длины пружины или смещению х точки: F=-kx), 2) Математический маятник. На материальную точку действуют сила натяжения Fн нити и сила тяжести mg. Их равнодействующая равна F =-kx, где k=mg/l, -kx=m(d2x/dt2),

Решение дифференциального уравнения второго порядка приводит к гармоническому закону x = А cos (ωt + φ0)- уравнение гармонического колебания. Здесь х – смещение тела от положения равновесия, А – амплитуда колебаний, т. е. максимальное смещение от положения равновесия, ω – циклическая или круговая частота колебаний, t – время. Величина, стоящая под знаком косинуса φ = ωt + φ0 называется фазой гармонического процесса. При t = 0 φ = φ0, поэтому φ0 называют начальной фазой. Минимальный интервал времени, через который происходит повторение движения тела, называется периодом колебаний T. Амплитуда и начальная фаза колебаний определяются начальными условиями движения, т.е. положением и скоростью материальной точки в момент t=0. ω определяет частоту колебаний системы и показывает, от каких факторов эта частота зависит: упругости и массы пружинного маятника в одном примере, длины нити и ускорения свободного падения — в другом. Период колебаний может быть найден из формулы T=2π/ω 0, период пружинного маятника: . период математического маятника: Физическая величина, обратная периоду колебаний, называется частотой колебаний: ν= 1/T Частота колебаний показывает, сколько колебаний совершается за 1 с. Единица частоты – герц (Гц). Частота колебаний связана с циклической частотой ω и периодом колебаний T соотношениями: ω=2πν.

Скорость

Ускорение Колебания, происходящие в системе при отсутствии внешних воздействий после какого-нибудь начального отклонения ее от состояния равновесия, называются свободными или собственными. Если в системе отсутствует переход механической энергии в другие ее виды (консервативная система), то свободные колебания будут незатухающими.

Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной.Классическим примером этого утверждения являются пружинный или математический маятники с пренебрежимо малым затуханием. существуют три основных фактора, определяющих процесс свободных колебаний систем, - масса, жесткость и демпфирование

Эффект затухания колебаний объясняется наличием трения; иногда его называют демпфированием. чаще используются чисто механические методы демпфирования.

Вопрос 31.

Процесс распространения колебательного движения в среде называется волновым процессом или просто волной. Простейший вид волнового движения – это волны, которые распространяются в одном направлении.

Волны - это изменение состояния среды (возмущения), распространяющиеся в этой среде и несущие с собой энергию и импульс без переноса вещества. Наиболее часто встречающиеся виды волн — упругие (звук) и электромагнитные (свет, радиоволны и другие). Несмотря на разную природу, все волны подчиняются общим закономерностям. Если возмущение ориентировано вдоль направления распространения, волна называется продольной (напр., звуковая волна в газе); если же возмущение лежит в плоскости, перпендикулярной направлению распространения, волна называется поперечной (напр., упругая волна, распространяющаяся вдоль струны, электромагнитная волна в свободном пространстве). Примером волнового движения может быть возмущение воды от падающих капель, которое распространяется в виде расширяющихся концентрических кругов.

Волновое уравнение и особенности волнового движения зависят от отдельных, разновидностей частей этого явления и от свойств среды, где происходит волновое движение. Волновое уравнение: A = A0 cos(ωt + kx) Волновое уравнение описывает распространение гармонических колебаний в пространстве. Характерными параметрами, описывающими гармоническую волну являются: A0 - амплитуда колебаний; ω - круговая частота (рад/с); период колебаний T (с), который связан с круговой частотой соотношением: T = 2π/ω; частота колебаний γ (Гц = 1/с) выражается через период: γ = 1/T; волновое число k = ω/v (где v- скорость распространения волны, измеряется в м/с); λ - длина (м) волны (λ = vT). Скорость распространения каждого вида волн зависит от свойств среды, в которой они распространяются.

Плотностью потока энергии волны называют вектор U, направленный в сторону распространения волны и равный по модулю отношению потока энергии dФw сквозь малый элемент площади dS поверхности к площади проекции этого элемента на плоскость, перпендикулярную направлению распространения волны:

Таким образом, вектор плотности потока энергии волны равен произведению вектора скорости распространения энергии волны и её объёмной плотности. Для упругих волн этот вектор был впервые введён в 1875 г. Н.А. Умовым и называется вектором Умова.

Вопрос 32

Многие колебательные системы могут одновременно участвовать в нескольких колебательных процессах. Под сложением колебаний понимают нахождение закона движения тела, участвующего одновременно в нескольких колебательных процессах. Любое движение можно представить как сумму двух или более движений, имеющих разные направления. Рассмотрим сложение двух одинаково направленных колебаний, которые совершаются вдоль оси OX декартовой системы координат с амплитудами A1 и A2, частотами ω1 и ω2, начальными фазами ϕ1 и ϕ2, соответственно: Х₁=А₁cos(ω₁t+φ₁), x₂=A₂ cos(ω₂t+φ₂), Результирующее движение также является одномерным и совер-шается вдоль той же OX декартовой системы координат. Для сложения одинаково направленных колебаний наиболее эф-фективным методом является метод векторной диаграммы. Для применения этого метода представим каждое колебание в виде вектора, длина которого равна амплитуде, вращающегося вокруг начала координат с частотой, равной частоте колебаний. Гармони́ческий ана́лиз (или Фурье́-ана́лиз) — раздел математики, в котором изучаются свойства функций с помощью представления их в виде рядов или интегралов Фурье. Также метод решения задач с помощью представления функций в виде рядов или интегралов Фурье. Метод анализа был основан на так называемых рядах Фурье. В соответствии с принципом интерференции ряд начинается с разложения сложной формы на простые — например, изменение земной поверхности объясняется землетрясением, изменения орбиты кометы — влиянием притяжения нескольких планет, изменение потока тепла — его прохождением сквозь препятствие неправильной формы из теплоизолирующего материала. Фурье показал, что сложная форма волны может быть представлена как сумма простых волн. Как правило, уравнения, описывающие классические системы, легко решаются для каждой из этих простых волн. Далее Фурье показал, как эти простые решения можно суммировать, чтобы получить решение всей сложной задачи в целом. (Говоря языком математики, ряд Фурье — это метод представления функции суммой гармоник — синусоид и косинусоид, поэтому анализ Фурье был известен также под названием «гармонический анализ».)

Вопрос 33

Установление гармонического спектра является основным приемом при анализе сложного колебания. Этот анализ делается с помощью специальных приборов —гармонических анализаторов. Они применяются и в медицине при исследовании, например, колебаний биопотенциалов головного мозга и др. Многие процессы человеческого организма являются периодическими: сердечные сокращения, дыхание, кровенаполнение сосудов и т. П. Гармонический анализатор - Устройство для автоматического определения коэффициентов ряда Фурье, в основу работы которого может быть положен принцип механический, оптический, фотоэлектрический и др.

Вопрос 34

Гидравлические потери или гидравлическое сопротивление — безвозвратные потери удельной энергии (переход её в теплоту) на участках гидравлических систем (систем гидропривода, трубопроводах, другом гидрооборудовании), обусловленные наличием вязкого трения[1][2]. Хотя потеря полной энергии — существенно положительная величина, разность полных энергий на концах участка течения может быть и отрицательной (например, при эжекционном эффекте). Потери энергии (уменьшение гидравлического напора) можно наблюдать в движущейся жидкости не только на сравнительно длинных участках, но и на коротких. В одних случаях потери напора распределяются (иногда равномерно) по длине трубопровода - это линейные потери; в других - они сосредоточены на очень коротких участках, длиной которых можно пренебречь, - на так называемых местных гидравлических сопротивлениях: вентили, всевозможные закругления, сужения, расширения и т.д., короче всюду, где поток претерпевает деформацию. Источником потерь во всех случаях является вязкость жидкости.Гидравлические потери принято разделять на два вида:
потери на трение по длине — возникают при равномерном течении, в чистом виде — в прямых трубах постоянного сечения, они пропорциональны длине трубы;
местные гидравлические потери — обусловлены т. н. местными гидравлическими сопротивлениями — изменениями формы и размера канала, деформирующими поток. Примером местных потерь могут служить: внезапное расширение трубы, внезапное сужение трубы, поворот, клапан и т. п.
Гидравлические потери выражают либо в потерях напора дельта h в линейных единицах столба среды, либо в единицах давления :( дельта) P: дельта h=дельта Р деленный на ро умноженный g , где (ро) — плотность среды, g — ускорение свободного падения.

Вопрос 35

Физические характеристики звука Одной из важнейших характеристик звуковых волн является спектр.Спектром называется набор различных частот, образующих данный звуковой сигнал. Спектр может быть сплошным или дискретным.Сплошной спектр означает, что в данном наборе присутствуют волны, частоты которых заполняют весь заданный спектральный диапазон.Дискретный спектр означает наличие конечного числа волн с определенными частотами и амплитудами, которые образуют рассматриваемый сигнал.По типу спектра звуки разделяются на шумы и музыкальные тона.Шум — совокупность множества разнообразных кратковременных звуков (хруст, шелест, шорох, стук и т.п.) — представляет собой наложение большого числа колебаний с близкими амплитудами, но различными частотами (имеет сплошной спектр).Физиологические характеристики звуковых колебаний Физическим характеристикам звуковых колебаний соответствуют определенные физиологические (субъективные) характеристики, связанные с восприятием его конкретным человеком. Это обусловлено тем, что восприятие звука — процесс не только физический, но и физиологический.Основными субъективными характеристиками звука можно считать громкость, высоту и тембр.Громкость (степень слышимости звука) определяется, как интенсивностью звука (амплитудой колебаний в звуковой волне), так и различной чувствительностью человеческого уха на разных частотах. Наибольшей чувствительностью человеческое ухо обладает в диапазоне частот от 1000 до 5000 Гц.При увеличении интенсивности в 10 раз уровень громкости увеличивается на 10 дБ. Вследствие этого, звук в 50 дБ оказывается в 100 раз интенсивнее звука в 30 дБ. высота звука определяется частотой звуковых колебаний, обладающих наибольшей интенсивностью в спектре.Тембр (оттенок звука) зависит от того, сколько обертонов присоединяются к основному тону и какова их интенсивность и частота. По тембру мы легко отличаем звуки скрипки и рояля, флейты и гитары, голоса людей 

Вопрос 36

Сложная структура крови приводит к тому, что описание ее динамических характеристик несколько отличается от описания традиционных жидкостей. Несмотря на это ученые смело используют некоторые приемы и упрощения из традиционной гидродинамики. Приведем пример. В наиболее простой и общей модели системы кровообращения сердце — это насос, создающий направленное движение крови в «трубах»: артериях, венах и капиллярах. Принято считать, что протекание крови ламинарное (то есть безвихревое), при этом профиль распределения скорости внутри сосудов носит параболический характер (рис. 1). Максимальная скорость течения наблюдается на оси сосуда, посередине, а на его краях жидкость неподвижна (см. также анимацию). Этот простой вид течения известен в физике как течение Пуазейля. В нормальных условиях ток крови почти во всех отделах сосудистого русла ламинарный. Это положение в настоящее время признается большинством исследо­вателей. Ламинарная форма движения жидкости подчиняется закону Пуазейля, который принято выражать следую­щей:

   

Формула(4)

    где, применительно к системе кровообращения, Q — ко­личество крови, протекающей через сосуд за единицу времени; r — радиус сосуда; АР — разница в давлении в начале и в  конце исследуемого участка сосудистого

русла; µ — вязкость крови; 

—  потеря давления, от­несенная к единице длины сосуда, называемая в физике градиентом давления.

    Для выражения зависимости линейной скорости кро­вотока от градиента давления и просвета  сосудистого русла формула  (4)  может быть преобразована следую­щим образом:



Формула(5)

или



Формула(6)

где v — линейная скорость кровотока; 

— пло­щадь поперечного сечения сосуда.

     Выражение 

есть не что иное, как проходимость данного участка сосудистой системы — величина, об­ратная тому общему гидравлическому сопротивлению R, которое данная трубка или система трубок оказыва­ет ламинарному движению жидкости Число, или, правильнее, критерий Рейно́льдса (), — безразмерная величина, характеризующая отношение нелинейного и диссипативного членов в уравнении Навье — Стокса^[1]. Число Рейнольдса также считается критерием подобия течения вязкой жидкости.Число Рейнольдса определяется следующим соотношением:

где  — плотность среды, кг/м³; — характерная скорость, м/с; — характерный размер, м; — динамическая вязкость среды, Н·с/м²; — кинематическая вязкость среды, м²/с() ; — объёмная скорость потока; — площадь сечения трубы.

Вопрос 37

Ультразвук - упругие волны высокой частоты, которым посвящены специальные разделы науки и техники. Человеческое ухо воспринимает распространяющиеся в среде упругие волны частотой приблизительно до 16 000 колебаний в секунду (Гц); колебания с более высокой частотой представляют собой ультразвук (за пределом слышимости). Обычно ультразвуковым диапазоном считают полосу частот от 18 000 герц. Хотя о существовании ультразвука ученым было известно давно, практическое использование его в науке, технике и промышленности началось сравнительно недавно. Сейчас ультразвук широко применяется в различных физических и технологических методах. По скорости распространения звука в среде судят о ее физических характеристиках. Измерения скорости на ультразвуковых частотах производятся с очень большой точностью; вследствие этого с весьма малыми погрешностями определяются, например, адиабатические характеристики быстропротекающих процессов, значения удельной теплоемкости газов, упругие постоянные твердых тел. Ультразвук по определению не воспринимается непосредствен-но органами чувств человека, и поэтому необходимо использовать какой-то физическийэффект или последовате-льность таких эффектов, чтобы действие ультразвукамогло проявиться, причем главным образом количественно. Таким образом,выбор метода для конкретной задачи производится сточки зрения удобства егоприменения, а также точности измерения интересующего параметраакустического поля. Применение АКУШЕРСТВО, ОФТАЛЬМОЛОГИЯ, ИССЛЕДОВАНИЕ ВНУТРЕННИХ ОРГАНОВ, ПРИПОВЕРХНОСНЫЕ И НАРУЖНЫЕОРГАНЫ, КАРДИОЛОГИЯ, НЕВРОЛОГИЯ, Болеутоляющее действие, Повышение подвижности суставов,Уменьшение мышечного спазма. Все процедуры должны выполнятся хорошо обученным персоналом или под егоруководством.Если следовать этим рекомендациям, то ультразвук можно эффективноиспользовать в медицине с большой уверенностью в его безопасности В технике ультразвук получают с помощью устройств, называемые УЗ-излучателями (генераторы УЗ). Наибольшее распространение получили электромеханические излучатели, основанные на явлениях магнитострикционного эффекта и обратного пьезоэлектрического эффекта.

Магнитострикционные излучатели применяются для генерирования низкочастотных ультразвуков (до 80 кГц).Пьезоэлектрические излучатели применяются для генерирования ультразвуков с частотами до 50 МГц.Явление обратного пьезоэлектрического эффекта заключается в механической деформации некоторых материалов (кристаллы кварца и турмалина, сегнетова соль, фосфорнокислый аммоний, керамический материал на основе титаната бария) под действием переменного электрического поля. Приемники ультразвука.В качестве приемников ультразвука на низких и средних частотах чаще всего применяют электроакустические преобразователи пьезоэлектрического типа. Такие приемники позволяют воспроизводить форму акустического сигнала, то есть временную зависимость звукового давления. В зависимости от условий применения приемники делают либо резонансными, либо широкополосными. Для получения усредненных по времени характеристик звукового поля используют термическими приемниками звука в виде покрытых звукопоглощающим веществом термопар или термисторов[4]. Интенсивность и звуковое давление можно оценивать и оптическими методами, например по дифракции света на УЗ.

Вопрос 38
Инфразвук (от