|
Николаева Т.М.,
2 ПОБ-нач-к-в
   Анализ аксиоматики школьных учебников в сравнении с аксиоматикой Д. Гильберта Анализ аксиоматики школьных учебников в сравнении с аксиоматикой Д. Гильберта
Автор
|
Аксиомы
|
Группы
|
Основные понятия
и отношения
|
Сходства и различия
|
Д. Гильберт
|
Аксиомы принадлежности:
1. Через две точки проходит одна и только одна прямая.
2. На каждой прямой лежат по меньшей мере две точки.
3. Существуют три точки, не лежащие на одной прямой.
4. Через каждые три точки, не лежащие на одной прямой, проходит одна и только одна плоскость.
5. Если две точки прямой принадлежат некоторой плоскости, то и все точки этой прямой принадлежат указанной плоскости.
6. Если две плоскости имеют общую точку, то они имеют по крайней мере еще одну общую точку.
7. Существует по крайней мере 4 точки, не лежащие в одной плоскости.
|
Первая группа
В них устанавливаются отношения между точками, прямыми и плоскостями.
|
Основные понятия:
точка,
прямая,
плоскость.
Основные отношения:
лежать между,
принадлежать,
конгруэнтность.
|
|
Аксиомы порядка:
1. Если точка В лежит между точками А и С, то она лежит между точками С и А.
2. Для любых двух точек прямой А и В существует на этой прямой такая точка С, что точка В лежит между точками А и С.
3. Из трех точек на прямой не более чем одна лежит между двумя другими.
4. Пусть точки А, В и С не лежат на одной прямой, и прямая не проходит ни через одну из этих точек. Если при этом прямая а пересекает отрезок АВ (то есть проходит через точку, лежащую между точками А и В), то она пересекает один из отрезков ВС или А С.
|
Вторая группа
Они определяют понятие «лежать между» и выражают свойства взаимного расположения точек на прямой и плоскости.
|
Аксиомы равенства (конгруэнтности):
1. На данной прямой по данную сторону от данной на ней точки можно отложить отрезок, равный данному, и притом единственным образом.
2. Два отрезка, порознь равные третьему, равны между собой.
3. Пусть на некоторой прямой точка В лежит между точками А и С и на некоторой другой или той же прямой точка В1 лежит между двумя точками А1 и С1. Если при этом отрезок АВ равен отрезку А1В1 и отрезок ВС равен В1С1, то АС = А1С1.
4. По данную сторону от данного луча можно отложить данный угол и притом единственным образом.
5. Два угла, порознь равные третьему, равны между собой.
6. Пусть А, В, С - три точки, не лежащие на одной прямой, А1, В1, С1- тоже три точки, не лежащие на одной прямой. Если при этом АВ = А1В1, 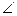 ВАС = ВАС = 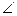 В1А1С1 то В1А1С1 то 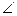 ABC = ABC = 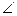 А1В1С1. А1В1С1.
|
Третья группа
Они определяют равенства отрезков и углов.
|
Аксиома непрерывности:
1. Если все точки прямой произвольным образом разбить на два класса так, что каждая точка первого класса лежит левее каждой точки второго класса, тогда непременно либо в первом классе есть самая правая точка (и во втором нет самой левой), либо во втором классе есть самая левая точка (и в первом нет самой правой).
|
Четвертая группа
Утверждается, что прямая не имеет проколов, что она непрерывна.
|
Аксиома параллельности:
1. В плоскости через точку вне данной прямой нельзя провести более одной прямой, не пересекающей данную прямую.
|
Пятая группа
В плоскость через точку вне данной прямой нельзя провести более одной прямой, не пересекающей данную прямую.
|
А. В. Погорелов
|
Аксиомы принадлежности:
1. Каковы бы ни были две точки, существует прямая, которая проходит через эти точки, и причем только одна.
2. На каждой прямой лежат, по крайней мере, две точки. Существуют три точки, не лежащие на одной прямой.
|
I группа
|
Основные понятия:
точка,
прямая,
плоскость
отрезок
полуплоскость.
Основные отношения:
лежать между,
принадлежать,
длина отрезков,
градусная мера углов.
|
��Аксиоматика Д. Гильберта состоит из 20 аксиом, поделенных на 5 групп.
У А. В. Погорелова 12 аксиом и 7 групп.
Сравнивая аксиоматику школьного курса в книге А.В. Погорелова и систему аксиом Гильберта выделяются основные понятия, используемые в них.
Так в школьном курсе основные понятия это точки, прямые, плоскости и отрезок, также используются понятия полуплоскости.
Гильберт использует следующие основные понятия: точка, прямая, плоскость.
Основные понятия в аксиоматике Гильберта - неопределяемые.
В связи с тем, что аксиоматика Погорелова школьная, то и доказываются аксиомы и решаются задачи практическим путём. А у немецкого учёного аксиомы выстроены и представлены по логике и любые задачи будут решаться логически.
|
Аксиомы порядка:
1. Из трех точек одна и только одна лежит между двумя другими.
2. Прямая разбивает множество точек плоскости, которые ей не принадлежат, на два подмножества (полуплоскости) так, что отрезок соединяет точки одной полуплоскости, не пересекает прямую, а отрезок, который соединяет точки разных полуплоскостей, пересекается этой прямой.
|
II группа
|
Аксиомы меры для измерения углов:
1. Каждый отрезок имеет определенную длину, большую нуля. Если точка С лежит на отрезке АВ, то длина отрезка АВ равна сумме длин отрезков АС и ВС.
2. Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 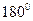 . Если луч с проходит между сторонами угла (ав), то градусная мера угла (ав) равна сумме градусных мер углов (ас) и (вс). . Если луч с проходит между сторонами угла (ав), то градусная мера угла (ав) равна сумме градусных мер углов (ас) и (вс).
|
III группа
|
Аксиома существования треугольника, равного данному:
1. Пусть АВС – треугольник и а – луч. Тогда существует треугольник 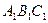 равного треугольнику АВС, в котором вершина равного треугольнику АВС, в котором вершина 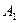 совпадает с началом луча а, вершина совпадает с началом луча а, вершина 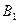 лежит на луче а, а вершина лежит на луче а, а вершина 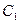 лежит в заданной полуплоскости относительно прямой, которая определяется лучом а. лежит в заданной полуплоскости относительно прямой, которая определяется лучом а.
|
IV группа
|
Аксиома существования отрезка данной длины:
1. Каким бы ни было действительное число 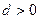 , существует отрезок длины d. , существует отрезок длины d.
|
V группа
|
Аксиома параллельности:
1. Через точку, которая не лежит на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.
|
VI группа
|
Пространственные аксиомы:
1. Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
2. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, переходящей через эту точку.
3. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.
|
VII группа
|
Л. С. Атаносян
|
Взаимное расположение точек и прямых:
1. Каждой прямой принадлежат по крайне мере две точки.
2. Имеются по крайне мере три точки, не лежащие на одной прямой.
3. Через любые две точки проходит прямая, и причём только одна
4. Из трёх точек прямой одна и только одна лежит между двумя другими.
5. Каждая точка O прямой разделяет ее на две части (два луча) так, чтобы любые две точки одного и того же луча лежат по одну сторону от точки О, а любые две точки разных лучей лежат по разные стороны от точки О.
6. Каждая прямая а разделяет плоскость на две части (две полуплоскости) так, что любые две точки одной и той же полуплоскости лежат по одну сторону от прямой а, а любые две точки разных полуплоскостей лежат по разные стороны от прямой а.
|
Первая группа
|
Основные понятия:
Точка
Прямая
Луч
Плоскость
Полуплоскость
Угол
Основные отношения
Лежать между
Принадлежать
Наложение
Совмещение
Равенство, равный данному
|
Рассматривая аксиоматику Гильберта и аксиоматику школьного учебника Л.С. Атанасяна можно прийти к следующим выводам.
Аксиоматика Л.С. Атанасяна состоит из 16 пунктов, разделенных на 3 группы.
Наибольшую схожесть аксиом Гильберта и аксиом Л.С. Атанасяна можно отметить в первой группе аксиом (аксиомы принадлежности), где почти для каждой аксиомы Гильберта можно соотнести аксиому из школьного учебника. Отличие состоит лишь в том, какие термины при этом используются. В школьном учебнике дана более упрощенная формулировка некоторых аксиом. В одной аксиоме также может обобщаться две аксиомы Гильберта.
Во второй группе аксиом (аксиомы порядка) в аксиоматике Гильберта выстроен целый ряд аксиом, в аксиоматике школьного учебника присутствует единственная схожая аксиома.
Третья группа аксиом школьного учебника в своей основе имеет такое понятие как наложение, т.е. отображение пространства на себя, чего нет в аксиомах Гильберта.
Четвертая группа аксиом Гильберта описывает длину отрезка и величину угла, а также свойства непрерывности расположения точек на прямой. В школьном учебнике кратко и просто сформулированы две аксиомы, связанные лишь с измерением отрезков.
Аксиомы пятой группы и Гильберта и в школьном учебнике представлены лишь одной аксиомой (аксиома параллельности). Различие в том, что Гильберт использует обозначения в аксиоме, а школьный учебник в более упрощенной форме описывает ту же самую аксиому.
|
Понятия наложения и равенства фигур
7. Если при наложении совмещаются концы двух отрезков, то совмещаются и сами отрезки.
8. На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.
9. От любого луча в данную полуплоскость можно отложить угол, равный данному неразвернутому углу, и притом только один.
10. Любой угол hkможно совместить наложением с равным ему углом h1k1 двумя способами: 1) так, что луч h совместится с лучом h1, а луч k – с лучом k1; 2) так, что луч h совместится с лучом k1, а луч k – с лучом h1.
11. Любая фигура равна самой себе.
12. Если фигура Ф равна фигуре Ф1, то фигура Ф1 равна фигуре Ф.
13. Если фигура Ф1 равна фигуре Ф2, а фигура Ф2 равна фигуре Ф3, то фигура Ф1 равна фигуре Ф3.
|
Вторая группа
|
Измерение отрезков
14. При выбрано единице измерения отрезков длина каждого отрезка выражается положительным числом.
15. При выбранной единице измерения отрезков для любого положительного числа существует отрезок, длина которого выражается этим числом.
16. Через точку, не летающую на данной прямой, проходит только одна прямая, параллельная данной.
|
Третья группа
|
Вывод:
Рассмотрев аксиоматику Д. Гильберта, А.В. Погорелова и Л.С. Атанасяна хочется выделить некоторые отличия по:
количеству аксиом и групп;
отношениям и понятиям.
Эти отличия вызваны тем, что А.В. Погорелов и Л.С. Атанасян создавали эти аксиоматические системы для школьных учебников, а значит, они должны быть адаптированы под возраст учащихся.
Все три аксиоматики опираются на полную систему аксиом евклидовой геометрии. Поэтому аксиомы всех 3 систем похожи по смыслу.
Таким образом, аксиоматика Гильберта хоть и схожа с аксиоматикой школьных учебников, но имеет при этом существенные отличия. По моему мнению, аксиомы учебника представлены в более упрощенном виде специально для усвоения их школьниками. Аксиомы построены с использованием других терминов, но, по сути, являются выводами или следствиями аксиом Гильберта.
Департамент образования города Москвы
Государственное автономное образовательное учреждение
высшего образования города Москвы
«Московский городской педагогический университет»
(ГАОУ ВО МГПУ)
Анализ аксиоматики школьных учебников в сравнении с аксиоматикой Д. Гильберта
по предмету
«Математика и элементы геометрии»
Выполнила студентка
Николаева Татьяна Михайловна
Группа: ПОБ-НАЧ-к-в
Проверила:
Чернова Александра Дмитриевна
2018 год |
 Скачать 34.41 Kb.
Скачать 34.41 Kb.

 Анализ аксиоматики школьных учебников в сравнении с аксиоматикой Д. Гильберта
Анализ аксиоматики школьных учебников в сравнении с аксиоматикой Д. Гильберта