Электротехника. Анализ цепи постоянного тока (задание 1, вариант 17 )

• Название: Анализ цепи постоянного тока (задание 1, вариант 17 )
• Анкор: Электротехника
• Дата: 27.09.2022
• Размер: 483.5 Kb.
• Имя файла: Электротехника.doc
• Тип: Анализ; #699528

Министерство образования и науки РФ

Кабардино-Балкарский государственный

Университет им. Х.М.Бербекова

Факультет информатики и управления

Кафедра САКТУ

Анализ цепи постоянного тока

(задание № 1, вариант №17 )

Выполнил: студент

2 курса

группы №1

Сабанов А.Х.

Проверил: доцент

Шаков Х.К.

Нальчик 2009

Исходные данные

На рис.1 приведена обобщенная схема цепи, а в таблице записаны значения параметров схемы в соответствии с вариантом задания.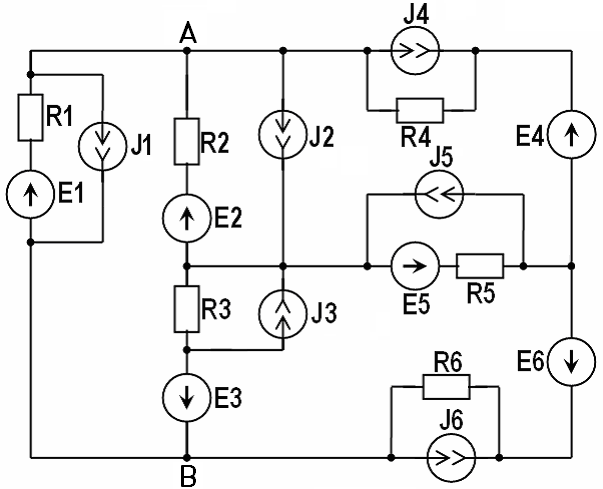



Рис.1. Обобщенная схема электрической цепи

Сопротивление R, Ом						Напряжение E, В						Ток J, А
R1	R2	R3	R4	R5	R6	E1	E2	E3	E4	E5	E6	J1	J2	J3	J4	J5	J6
7	2	5	6	3	2	0	0	15	0	0	0	3	0	0	0	0	9

Для обобщенной схемы и заданных значений параметров:

1. 
   составить расчетную схему электрической цепи;
   
2. 
   записать систему уравнений Кирхгофа для определения токов в ветвях схемы;
   
3. 
   определить значения токов в ветвях схемы по методу контурных токов;
   
4. 
   выполнив эквивалентное преобразование «треугольник – звезда», трансформировать расчетную схему в схему с двумя узлами и определить токи в ветвях схемы на основе метода узловых потенциалов;
   
5. 
   определить значение тока в ветви с резистором R6 по методу эквивалентного генератора;
   
6. 
   рассчитать напряжение между точками A и B, изображенными на рис.1;
   
7. 
   выполнить проверку баланса мощностей.
   

1. 
   Расчётная схема
   

В соответствии со значениями параметров элементов схемы, представленными в таблице, в расчетную схему следует включить 6 резисторов, 1 источник ЭДС и 2 источника тока.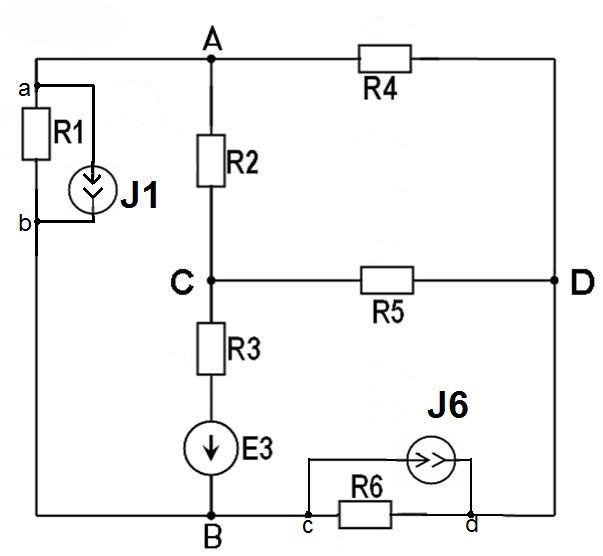



Рис.2.Расчётная схема, заданная по варианту

Анализировать схему будет проще, если источники тока заменить эквивалентными источниками ЭДС. Выполним такое преобразование для источников тока J1 и J6.

Эквивалентные значения ЭДС E1 и E6 будут равны соответственно

E1_э= R1 *J1; E1_э=7*3=21 (В);

E6_э=R6*J6; E6_э=2*9=18 (B).
На рис.3 представлена расчетная схема с учетом эквивалентного преобразования источников энергии.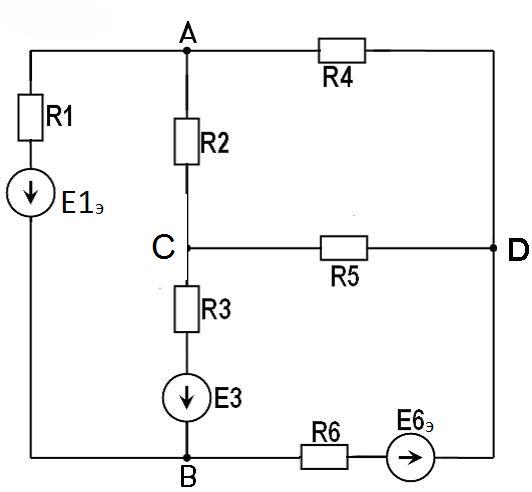



Рис.3. Расчетная схема электрической цепи

2. Система уравнений Кирхгофа для определения токов в ветвях схемы

Расчетная схема имеет 6 ветвей и 4 узла (см.рис.3). Следовательно, система должна включать 6 уравнений.

Произвольно выбираем направление протекания тока для каждой ветви. На рис.4 показаны принятые направления протекания токов в ветвях схемы. Закруглённые стрелки показывают принятые направления обхода контуров.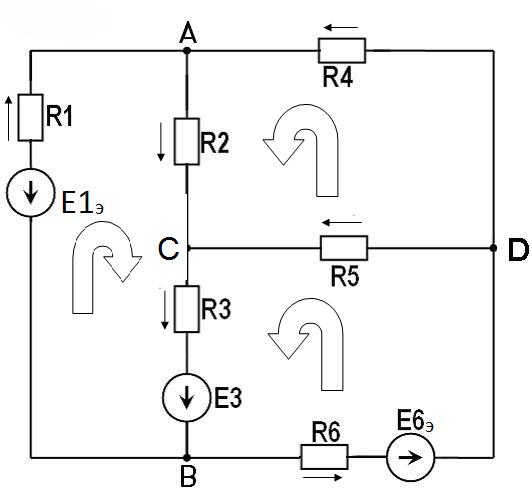



Рис.4. Расчетная схема электрической цепи с принятыми

направлениями протекания в ней токов
Так как в схеме 4 узла, то по первому закону Кирхгофа составляем три уравнения для узлов A, С и B.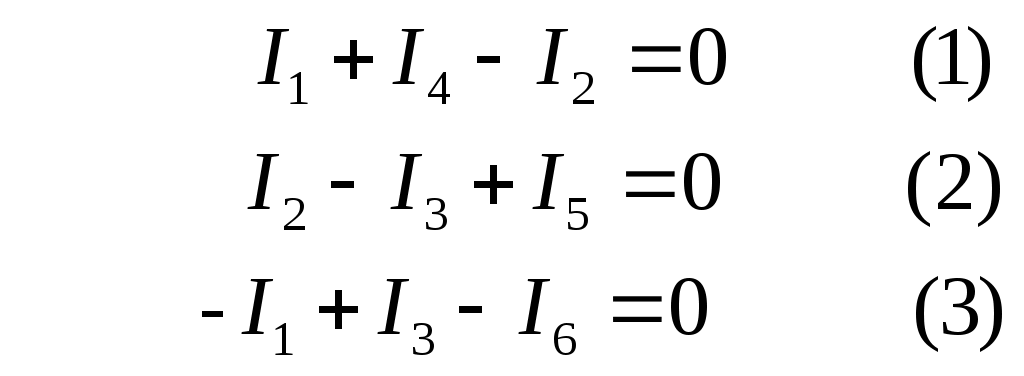



Еще 3 уравнения составим по второму закону Кирхгофа для левого контура (включающего ветви с резисторами R1, R2 и R3), правого верхнего и правого нижнего контура: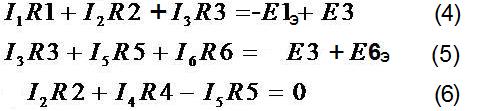



Для определения токов в ветвях схемы имеем систему уравнений (1)-(6):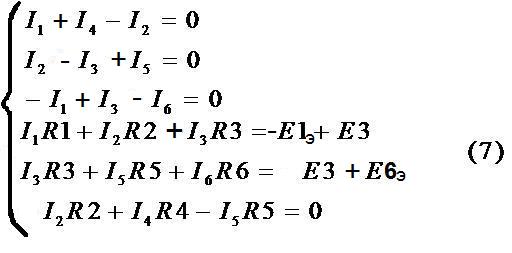



3.Анализ схемы методом контурных токов

На рис.5 показаны произвольно выбранные направления протекания контурных токов в непересекающихся контурах схемы.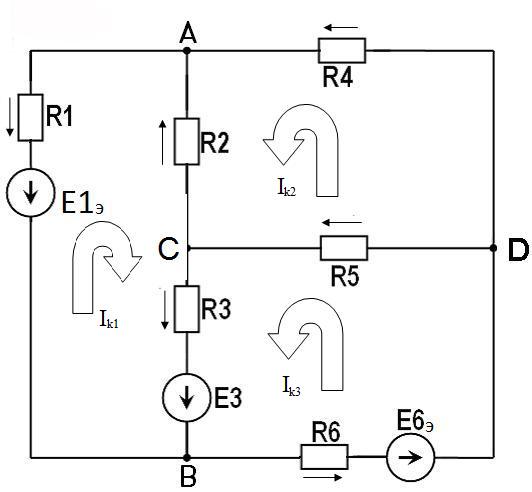



Рис.5.Схема цепи с произвольными направлениями контурных токов

С учетом принятых направлений контурных токов запишем систему уравнений: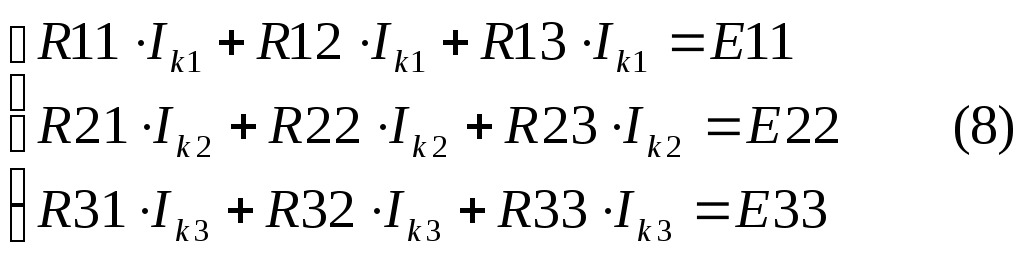



В системе уравнений (8)

R11, R22 и R33 – собственные сопротивления соответственно первого, второго и третьего контуров;

R12=R21, R13=R31, R23=R32 являются смежными сопротивлениями между соответственно первым контуром и вторым, первым и третьим, а также вторым и третьим;

E11, E22 и E33 – контурные ЭДС.

Определим значения параметров, входящих в систему уравнений (8).

R11 = R1 + R2 + R3; R11 = 7 + 2 + 5 = 14 (Ом)

R22 = R2 + R4 + R5; R22 = 2 + 6 + 3 = 11 (Ом)

R33 = R3 + R5 + R6; R33 = 5 + 3 + 2 = 10 (Ом)

R12 = R21 = R2; R12 = R21 = 2 (Ом);

R13 = R31 = R3; R13 = R31 = 5 (Ом);

R23 = R32 = -R5; R23 = R32 = -3 (Ом);

Для смежных сопротивлений R23 и R32 записаны отрицательные значения, т.к. через сопротивление R5 контурные токи протекают в противоположных направлениях, а для смежных сопротивлений R12=R21 и R13=R31 записаны положительные направления, т.к. через другие смежные сопротивления контурные токи протекают в одинаковых направления.

E11 =-E1_э + E3; Е11 = -21 + 15 =-6 (B); E22 = 0; т.к. в контуре отсутствует источники энергии;

E33 = E3 + E6_э; Е33 = 15 + 18 = 33 (B);

При подстановке вычисленных параметров в систему уравнений (8) получаем: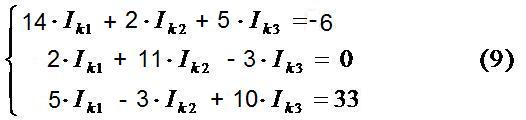



Вычислим значения главного определителя Δ системы уравнения (9) и определителей Δ₁, Δ₂, Δ₃: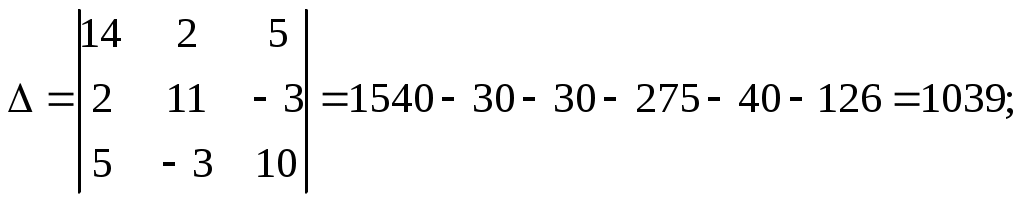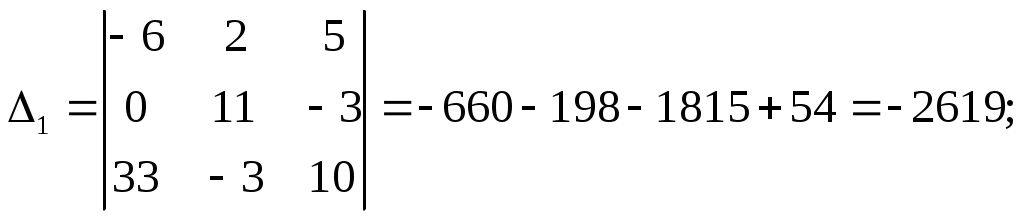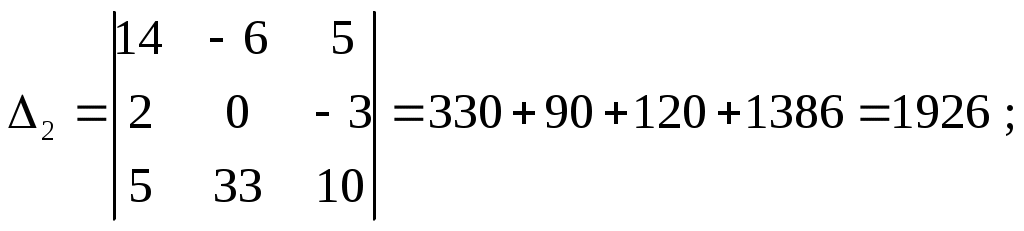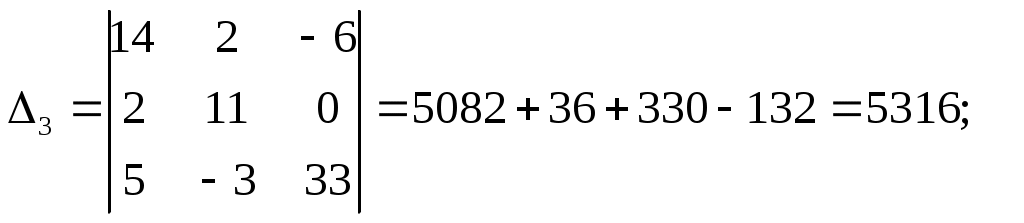









Значения контурных токов



Определение значения токов в ветвях схемы






Действительные направления протекания токов показаны на рисунке 6.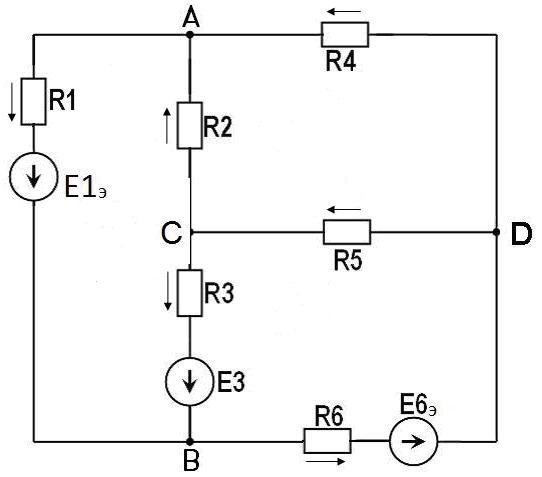



Рис.6.Схема с действительными направлениями токов в ветвях

4. Расчет схемы методом узловых потенциалов с дополнительным эквивалентным преобразованием

В расчетной схеме (см.рис.3) резисторы R2, R4 и R5 соединены по схеме «треугольник». Для этого соединения осуществим эквивалентное преобразование « ».

На рис.7 представлена часть анализируемой схемы, подвергаемая эквивалентному преобразованию.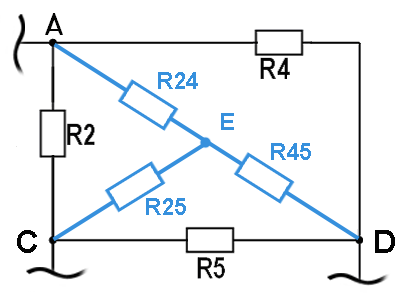



Рис.7. Участок эквивалентного преобразования «треугольник-звезда»

Определим значения R24, R45 и R25:



С учетом выполненного преобразования расчетная схема имеет вид, представленный на рис.8.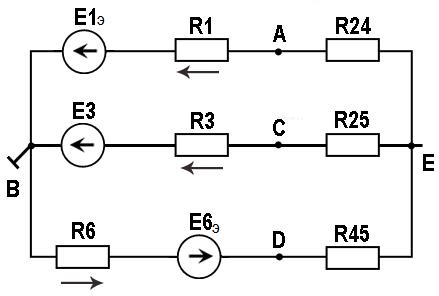



Рис.8. Расчетная схема после эквивалентного преобразования

Преобразованная схема имеет два узла (в точках «B» и «E»), к которым подключены три ветви. Принимаем потенциал точки «B» равным нулю. Для определения потенциала в точке «Е» можно использовать уравнение для этого узла:

G_∑•φ_Е=I_Е(10)

В уравнений (10):

G_∑ - узловая проводимость, определяемая суммой проводимостей ветвей, сходящихся в узле «Е»;

I_Е – узловой ток, равный алгебраической сумме слагаемых, каждое из которых равно произведению ЭДС ветви на проводимость соответствующей ветви.

Обозначим проводимости верхней, средней и нижней ветви на рис.6 соответственно как G1, G3 и G6. Эти параметры, очевидно, можно вычислить:







Определим значение G_∑и I_E:

G_∑ =

G_∑=



В последнем уравнений два слагаемых имеют знак «-», т.к. в верхней и средней ветви стрелка в условном обозначении ЭДС направлена от узла «Е», последнее слагаемое имеет знак «+», т.к. в нижней ветви стрелка в условном обозначении ЭДС направлена к узлу «Е».



Из (10) следует, что



Потенциалы точек «B» и «E» известны, поэтому токи в ветвях можно вычислить по закону Ома:



В преобразованной схеме на рис.6 отсутствуют ветви с резисторами R2, R4 и R5. Чтобы определить значение токов в ветвях с этими резисторами надо определить потенциалы точек «A», «C» и «D».

Потенциал φ_Aниже потенциала φ_Е (с учетом направления тока I₁ на рис.8) на значение, определяемое падением напряжения на резисторе R24 следовательно,



Аналогично находим

Определяем значения токов



5. Определение тока в ветви с резистором R6 методом эквивалентного генератора

При использовании метода эквивалентного генератора надо для анализируемой ветви схемы определить напряжение холостого хода и входное сопротивление.

На рис.7 показана схема для определения напряжения холостого хода.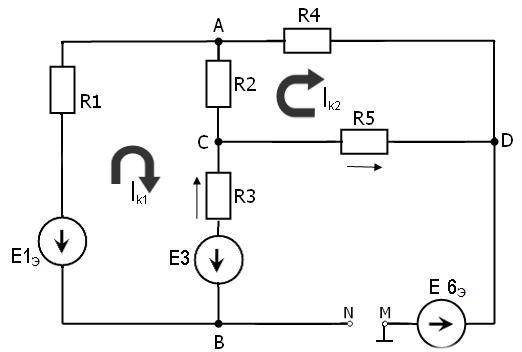



Рис.9. Схема для определения напряжения холостого хода

Эта схема отличается от расчётной схемы тем, что в ней исключен участок с резистором R6 и точки разрыва обозначены буквами М и N.

Для напряжения холостого хода получаем



Принимаем . Определим потенциал .

В схеме только два непересекающихся контура, поэтому расчет цепи выполним методом контурных токов.

Определим значения собственных сопротивлении, смежного сопротивления и контурных ЭДС (аналогично тому, как это было сделано в третьем разделе задания).

R11 = R1 + R2 + R3; R11 = 7 + 2 + 5 = 14 (Ом)

R22 = R2 + R4 + R5; R22 = 2 + 6 + 3 = 11 (Ом)

R12 = R21 = -R2; R12 = R21 = -2 (Ом);

E11 = -E1э + E3; E11 = -21 + 15 = -6 (B);

E22 = 0; E22 = 0 (В);

Система контурных уравнений имеет вид: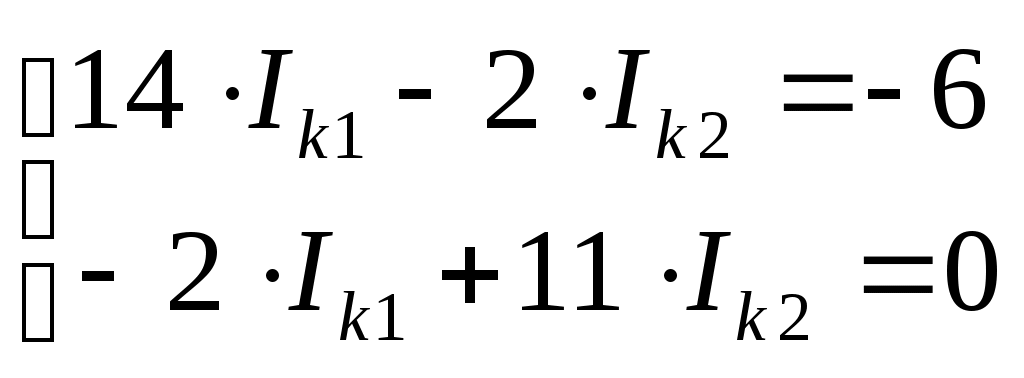

(11)

Вычислим значения главного определителя 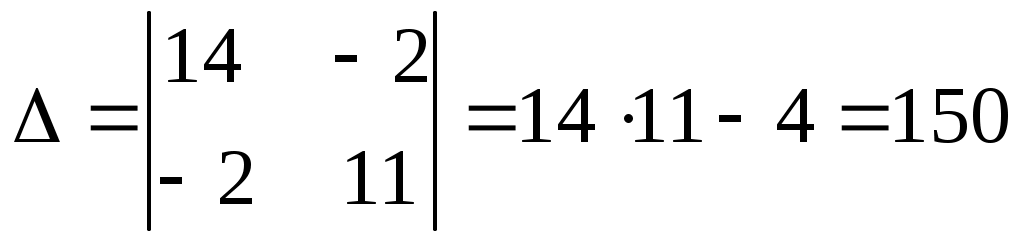Δ и определителей Δ₁ и Δ₂.







Получаем для контурных токов





Рассматривая изменение потенциала в направлении от точки «М» к точкам «Д», «С», «В», «N», получаем что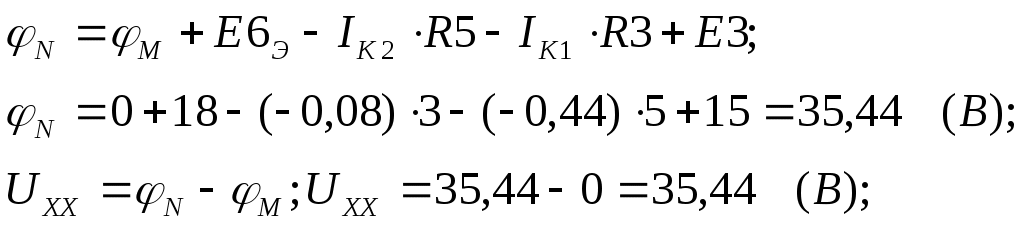



Для определения входного сопротивления из схемы рис.9 надо удалить источники напряжения (источники ЭДС) и вычислить эквивалентное сопротивление относительно входных зажимов N и М. Соответствующая схема показана на рис.10.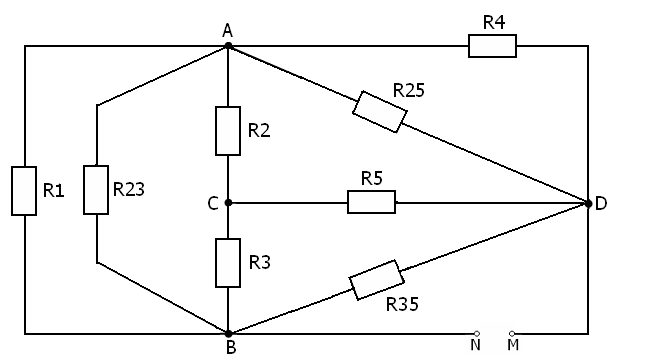



Рис.10. Схема для расчета входного сопротивления

Для определения R_BX предварительно выполним эквивалентное преобразование « ».





С учетом преобразования имеем: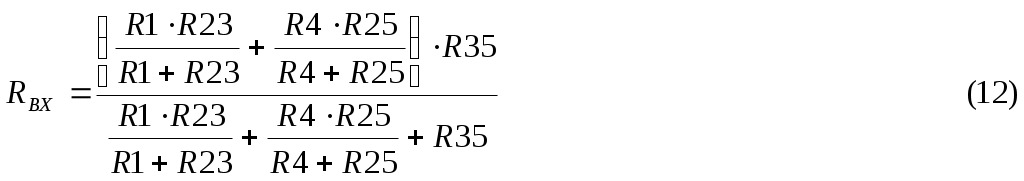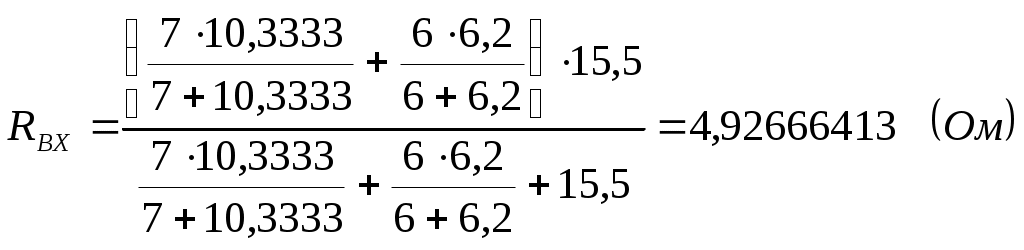





Значение тока I₆ находим по соотношению






Полученный ток I₆ соответствует полученным другими методами значениям того же тока I₆. Это подчёркивает высокую точность вычислений и достоверность значения.

6. Расчет напряжений между точками «А» и «В»


Потенциалы точек «А» и «В» уже были определены в четвертом разделе, поэтому



Проверим достоверность этого значения, используя результат определения

тока I₁ в разделе 3: I₁ = - 2,5207 (A)
В соответствии с рис.3
φ_А= φ_B-E1Э+ I₁·R1 (14)
Принимаем φ_B = 0, тогда
φ_A=0-21+2,5207·7= -3,3551(В)
Поэтому
U_AB= φ_A - φ_B ; U_AB= -0,3552-0=-3,3552 (В).

7. Проверка баланса мощностей

Генерируемая мощность (см. рис.6) по результатам расчета в третьем разделе значений токов:

Pген = E1э·I₁ + E3·I₃ + E6э·I₆ (15)

Pген = 21· 2,5207 + 15·2,5958 + 18·5,1165 = 183,9687 (Вт)

Потребляемая мощность:

P= I₁²·R1+I₂² ·R2+I₃² ·R3+I₄² ·R4+I₅² ·R5+I₆² ·R6 (16)

P= 2,5207² · 7 + 0,667² · 2 + 2,5958² · 5 + 1,8537² · 6 +

+ 3,2628² · 3 + 5,1165² · 2 = 183,97012 (Вт)

Относительная погрешность расчета мощностей:





Список использованных источников

1. 
   Бессонов Л.А. Теоретические основы электротехники.
   

Электрические цепи: Учебник ­­– 9-е изд., -М.:ВШ, 1996.-638 с.: илл.

2. 
   Конспект лекций по дисциплине «Электротехника и электроника».