ер. вар_21 задача 1 (1). Задание Расчет электрической цепи постоянного тока
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
Задание 1. Расчет электрической цепи постоянного токаЗадана схема электрической цепи (рис. 1) и численные значения ее параметров, приведенные в таблице 1. Требуется: 1. Начертить граф цепи, деревья и дополнения. Количество деревьев должно быть не менее количества узлов, уменьшенного на единицу. Составить топографические матрицы цепи. 2. Определить токи во всех ветвях методом узловых потенциалов. 3. Определить токи во всех ветвях методом контурных токов, сравнить с результатами расчета по п.2. 4. Определить показания вольтметров. 5. Проверить баланс мощностей. 6. Рассчитать потенциалы в точках соединения элементов внешнего контура цепи, построить потенциальную диаграмму. Выбрать оптимальную точку заземления. 7. Рассчитать значение тока методом эквивалентного источника тока. 8. Рассчитать значение тока методом эквивалентного источника ЭДС. Таблица 1 – Исходные данные
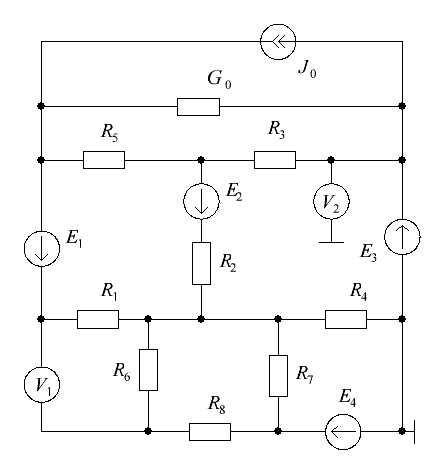 Рисунок 1 – Схема электрической цепи Решение: 1. Так как сопротивление вольтметров бесконечно велико при расчете их можно исключить. Источник тока заменим источником ЭДС: Выполним эквивалентное преобразование сопротивлений: 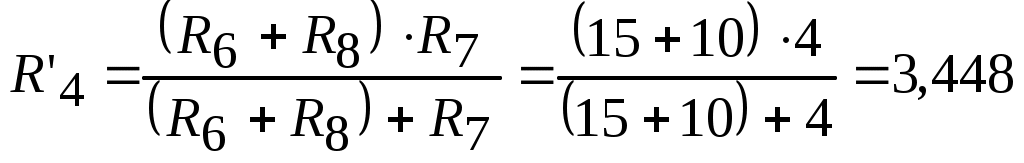 Ом. Ом.Расчетная схема электрической цепи изображена на рисунке 2. 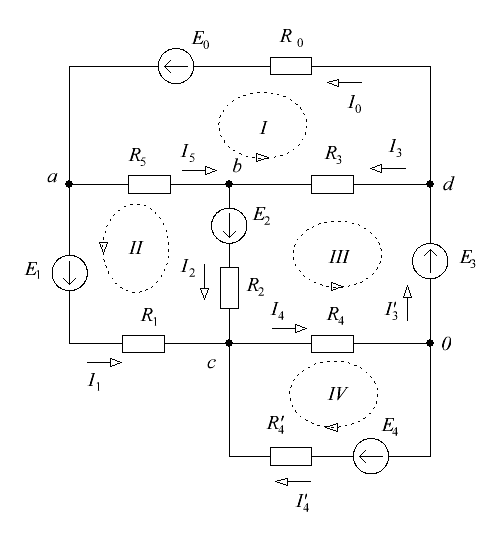 Рисунок 2 – Расчетная схема электрической цепи Составим систему уравнений, необходимую для определения токов в ветвях цепи, по законам Кирхгофа. Для определения токов в ветвях цепи по законам Кирхгофа необходимо составить  , ,2. Граф электрической цепи, деревья (выделены жирным) и дополнения (пунктирные линии), соответствующие расчетной схеме изображены на рисунках 3-6. 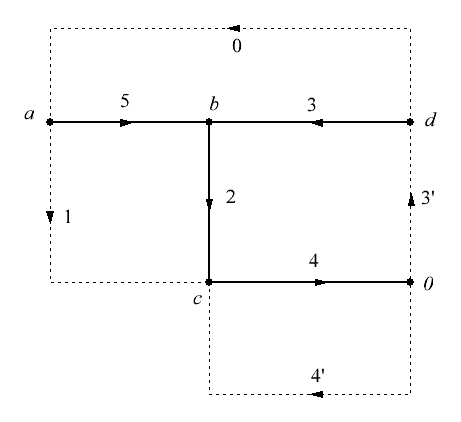 Рисунок 3 – Граф расчетной цепи 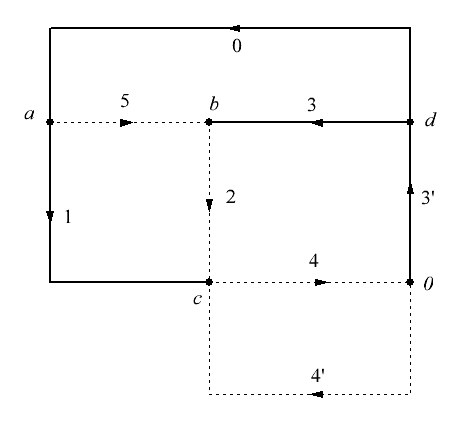 Рисунок 4 – Граф расчетной цепи 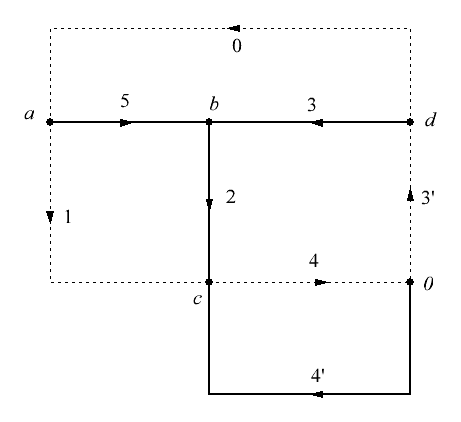 Рисунок 5 – Граф расчетной цепи 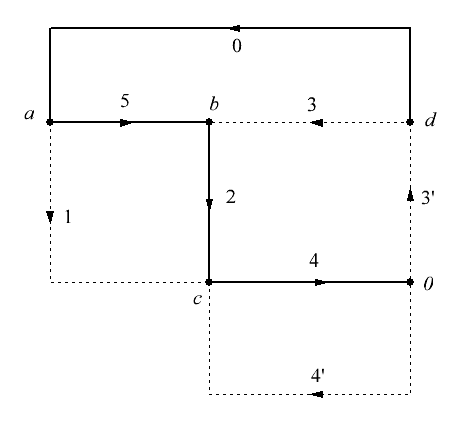 Рисунок 6 – Граф расчетной цепи 3. Составим топографические матрицы цепи. Составим матрицу соединений. Выбираем узлы a, b, с и d, для которых  Составим матрицу главных сечений.  Составим матрицу главных контуров  4. Выполним расчет цепи методом контурных токов. Выбираем направление контурных токов (см. рис. 2). Для рассматриваемой трехконтурной цепи система уравнений относительно контурных токов, примет вид: 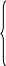 , ,Подсчитаем значения коэффициентов системы: – собственные сопротивления контуров: – общие сопротивления контуров: – контурные ЭДС: После подстановки численных значений коэффициентов и необходимых преобразований система уравнений примет вид: 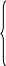 , ,В результате расчета системы уравнений с использованием ЭВМ получим: В соответствии с принятыми положительными направлениями токов в ветвях вычисляем их значения: 5. Выполним расчет цепи методом узловых потенциалов. Примем потенциал узла 0 равным нулю ( 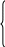 , ,Рассчитаем значения коэффициентов системы: – собственная проводимость узлов: – общие проводимости узлов: – узловые токи: После подстановки численных значений коэффициентов система уравнений примет вид 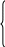 , ,В результате расчета системы уравнений с использованием ЭВМ получим: По закону Ома рассчитаем токи ветвей: Ток I'3 определим из уравнения, составленного по первому закону Кирхгофа: Сравним значения токов, рассчитанных разными методами. Результаты сравнения представлены в виде таблицы (см. таблицу 2). Таблица 2 – Сравнение результатов расчета
6. Определим показания вольтметров из уравнений, составленных по второму закону Кирхгофа: где 7. Проверим соблюдение баланса мощностей. где 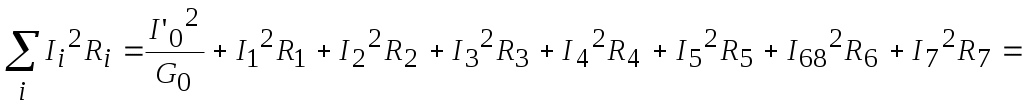 где В результате следовательно, баланс мощностей соблюдается. 8. Построим потенциальную диаграмму для внешнего контура цепи (см. рис. 7). 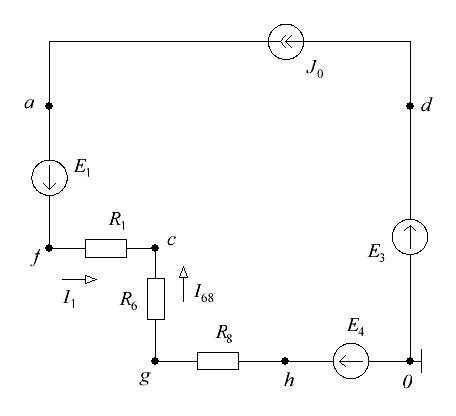 Рисунок 7 – Внешний контур исходной электрической цепи Определим потенциалы узлов (точек): Таким образом, оптимальной точкой заземления является т. 0. Потенциальная диаграмма изображена на рисунке 8. 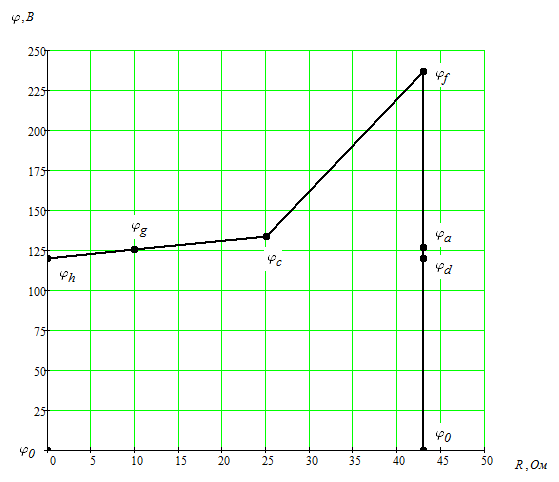 Рисунок 8 – Потенциальная диаграмма 9. Методом эквивалентного источника тока определим ток в ветви с резистором R3. Закоротим зажимы резистора и обозначим ток короткого замыкания (см. рис. 9). 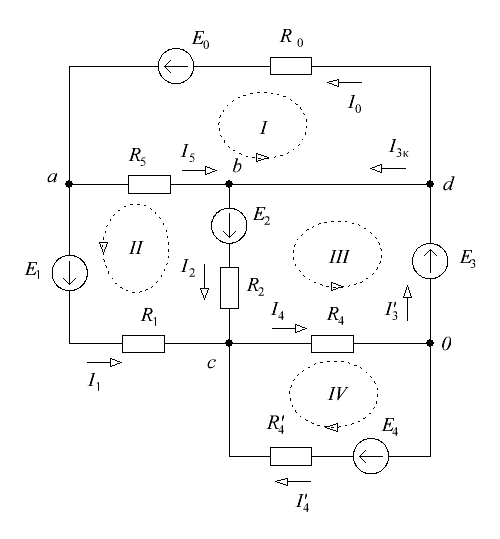 Рисунок 8 – Схема цепи для расчета тока методом эквивалентного источника тока Определим ток эквивалентного генератора, используя метод контурных токов (аналогично п. 4). Выбираем направление контурных токов (см. рис. 8). Для рассматриваемой трехконтурной цепи система уравнений относительно контурных токов, примет вид:  , ,Подсчитаем значения коэффициентов системы: – собственные сопротивления контуров: – общие сопротивления контуров: – контурные ЭДС: После подстановки численных значений коэффициентов и необходимых преобразований система уравнений примет вид:  , ,В результате расчета системы уравнений с использованием ЭВМ получим: Таким образом, Для определения входного сопротивления эквивалентного генератора исключим из цепи все источники ЭДС и выполним преобразование цепи (замена треугольника сопротивлений эквивалентной звездой). Схема цепи для определения входного сопротивления после преобразования изображена на рисунке 9. Входное сопротивление: 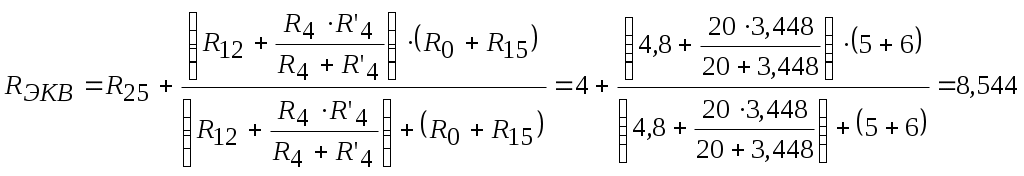 Ом. Ом.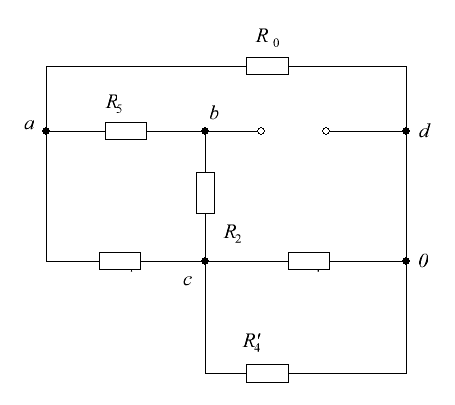 Рисунок 9 – Схема цепи для определения входного сопротивления эквивалентного генератора Схема эквивалентного генератора изображена на рисунке 10. 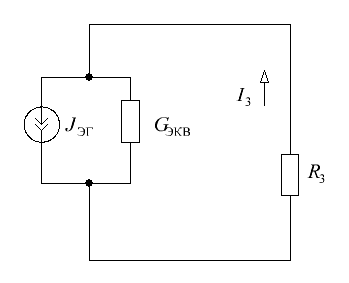 Рисунок 10 – Схема эквивалентного генератора тока В результате искомый ток равен 10. Методом эквивалентного источника ЭДС определим ток в ветви с резистором R3. Изобразим схему электрической цепи без учета резистора R3 (см. рис. 11). Расчет выполним методом узловых потенциалов аналогично п.5. Схема эквивалентного генератора изображена на рисунке 11. 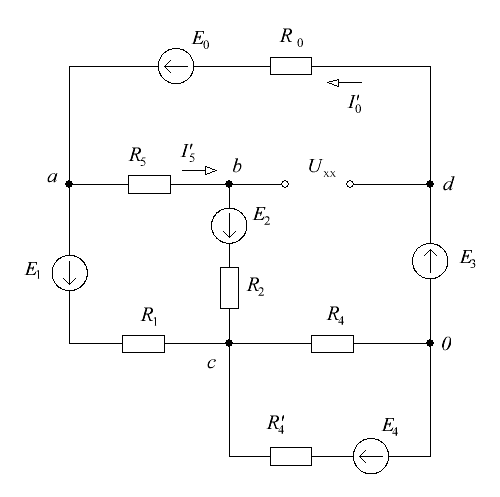 Рисунок 11 – Схема цепи для расчета тока методом эквивалентного источника ЭДС Примем потенциал узла 0 равным нулю (  , ,Рассчитаем значения коэффициентов системы: – собственная проводимость узлов: – общие проводимости узлов: – узловые токи: После подстановки численных значений коэффициентов система уравнений примет вид  , ,В результате расчета системы уравнений с использованием ЭВМ получим: ЭДС эквивалентного генератора: где 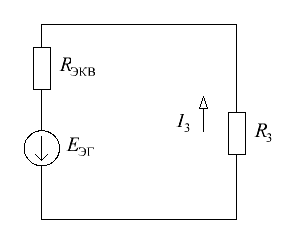 Рисунок 12 – Схема эквивалентного генератора ЭДС Ток в резисторе R3 методом эквивалентного генератора ЭДС: Список используемой литературыЭлектротехника. / Под ред. В. Г. Герасимова. - М.:Высшая школа, 1985. Нейман Л.Р. Демирчян К.С. Теоретические основы электротехники. Т. 1-2. - Л.: Энергоиздат, 1981. Борисов Ю.М. Липатов Д.Н. Зорин Ю.Н. Электротехника - М.: Энергоатомиздат,1985. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. - М.: Высш. школа.1984. |
