Конспект_3. Потенциальная диаграмма. Законы Кирхгоффа

• Название: Потенциальная диаграмма. Законы Кирхгоффа
• Анкор: Конспект_3
• Дата: 04.02.2022
• Размер: 1.02 Mb.
• Имя файла: Конспект_3.doc
• Тип: Закон; #351708
• страница: 1 из 2

§2.5. Потенциальная диаграмма. Законы Кирхгоффа.

Потенциальная диаграмма представляет собой график изменения потенциалов точек цепи от величины сопротивлений участков между этими точками. Для построения потенциальной диаграммы одну из точек электрической цепи условно заземляют (потенциал ее принимают равным нулю), а потенциал остальных точек равен напряжению между этими точками и заземленной точкой. Потенциальная диаграмма изображается в виде ломаной линии.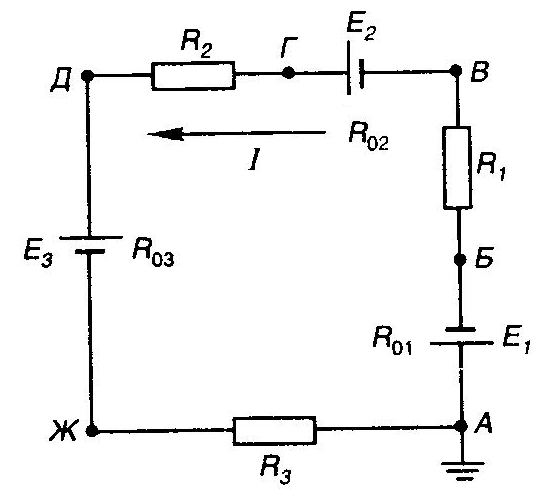



Рис. 2.6.

Элементы электрической цепи. В схемах электрических цепей можно выделить характерные элементы: ветвь, узел, контур.

Ветвью электрической цепи называется ее участок, на всем протяжении которого величина тока имеет одинаковое значение.

Узлом электрической цепи (узловой точкой) называется место соединения ветвей. В узловой точке сходятся минимум три ветви (проводника) (рис. 2.8,а).

Контуром электрической цепи называют замкнутый путь, в который могут входить несколько ветвей (рис. 2.8, б).

Ветви, содержащие источник электрической энергии, называются активными; а ветви, не содержащие источников, называются пассивными.

Первый закон Кирхгофа В разветвленной цепи ток в различных ветвях может иметь различное значение. Сумма токов, входящих в узловую точку разветвленной цепи, должна быть равна сумме токов, выходящих из этой точки.

На рис. 8, а показана узловая точка А цепи, для которой можно записать:

I₁+I₃+I₅=I₂+I₄или I₁-I₂+I₃- I₄+I₅=0, т. е. = 0. (2.31)

Выражение (2.7.1.) представляет собой математическую запись первого закона (правила) Кирхгофа. Первый закон Кирхгофа формулируется: алгебраическая сумма токов в ветвях, соединенных в один узел, равна нулю. Токи, входящие в узел, принято считать положительными, а выходящие из узла – отрицательными.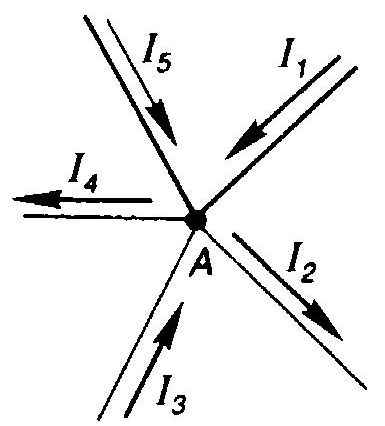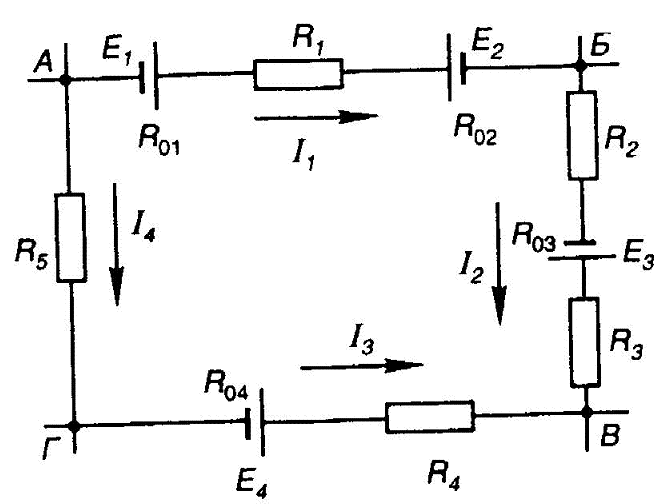



а) б)

Рис. 2.8.

Второй закон Кирхгофа устанавливает зависимость между ЭДС и падениями напряжения в замкнутом контуре любой электрической цепи. Согласно второму закону Кирхгофа алгебраическая сумма ЭДС в замкнутом контуре электрической цепи равна алгебраической сумме падений напряжений на всех участках этой цепи, т. е.

∑E = ∑IR (2.32)

Выражение (2.32.) представляет собой математическую запись второго закона (правила) Кирхгофа.

Для определения знаков в алгебраической сумме произвольно задаются направлением обхода контура: по часовой или против часовой стрелки.

ЭДС источника, совпадающая с выбранным направлением обхода контура, считается положительной, а не совпадающая – отрицательной.

Падение напряжения на сопротивлении резистора считается положительным, если ток, протекающий через резистор, совпадает с выбранным направлением обхода контура, или отрицательным – если не совпадает.

Для электрической цепи, изображенной на рис. 2.8, б, второй закон Кирхгофа записывается так:

Направление обхода выбрано по часовой стрелке. Точки А, Б, В и Г – узловые.

§2.6. Соединения резисторов.

Законы Кирхгофа позволяют анализировать и рассчитывать электрические цепи с одним источником при различных соединениях резисторов.

Последовательным соединением участков электрической называют соединение, при котором через все участки цепи проходит один и тот же ток (рис. 2.9). Напряжение на каждом последовательно включенном участке пропорционально величине сопротивления этого участка.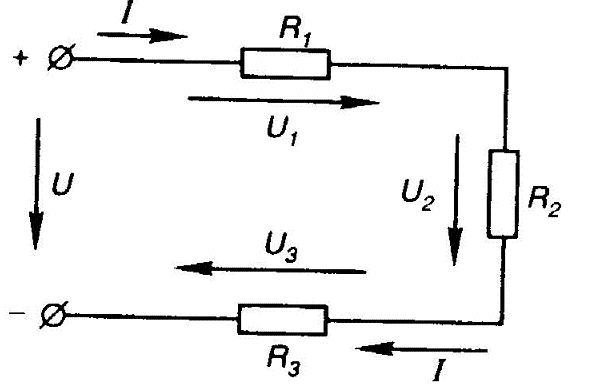



Рис. 2.9.

При последовательном соединении потребителей с сопротивлениями R_1,R₂и R₃ напряжение на их зажимах равно:



Воспользовавшись вторым законом Кирхгофа для рассматриваемой цепи (рис.9.), можно записать:



Или



Откуда

(2.33)

т. е. общее (эквивалентное) сопротивление последовательно включенных потребителей равно сумме сопротивлений этих потребителей.

Ток в цепи последовательно включенных потребителей (рис. 2.9.) определяется выражением:



Из этого выражения следует, что при изменении сопротивления хотя бы одного потребителя изменяется ток цепи, а следовательно, и режим работы (напряжение) всех последовательно включенных потребителей (резисторов).

Характерно, что при последовательном соединении потребителей на большем сопротивлении тратится большая мощность:



Распределение напряжений, пропорциональное сопротивлениям последовательно соединенных резисторов, используется в работе потенциометра (делителя напряжения). В качестве потенциометра можно использовать реостат с подвижным контактом, 'Включенным как показано на рис. 2.10.

Меняя сопротивление реостата, можно плавно изменять напряжение U₂ на потребителе от величины входного напряжения U₂ (движок реостата в точке А) до нуля (движок реостата в точке Б). Потребитель подключается к клеммам 2'-2".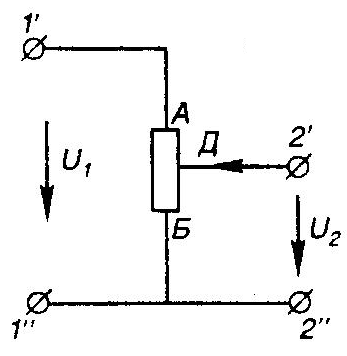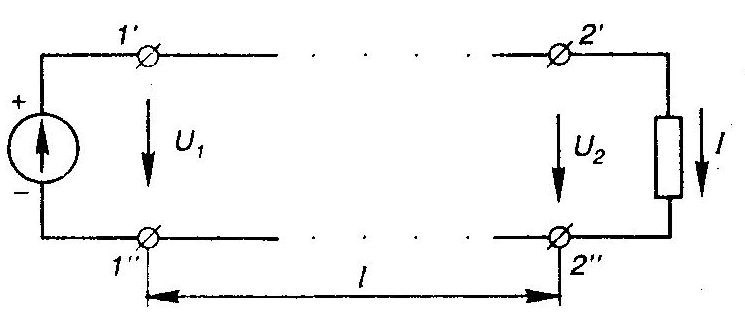



Рис. 2.10. Рис. 2.11.

Делитель напряжения может состоять из нескольких резисторов с постоянными сопротивлениями, соединенными последовательно. Напряжение можно снимать с каждого резистора или группы резисторов.

В линиях электропередачи (ЛЭП) электрической энергии на, расстояние соединительные провода включаются последовательно с потребителями (рис. 2.11).

Так как провода линии электропередачи обладают сопротивлением (двухпроводная линия), то при прохождении тока по проводам происходит потеря напряжения на них . За счет этой потери напряжение в конце линии электропередачи U₂меньше, чем напряжение в начале линииU₁. Величина потери напряжения в проводах

∆U=U₁ – U₂ = I•R_пр. (2.34)

Как видно из (2.6.2.), потеря напряжения в проводах зависит тока потребителя I (нагрузки).

Для того чтобы увеличение тока в линии не приводило к значительной потере напряжения в ней и к ощутимому уменьшению напряжения на потребителе U₂, расчет сечений проводов ЛЭП производят с учетом допустимой потери напряжения

е% = (2.35)

Допустимая потеря напряжения в длинных ЛЭП – до 10%.

Расчет сечения проводов (двухпроводной линии) по допустимой потере напряжения производят по следующему выражению!

(2.36)

где S – сечение проводов ЛЭП, мм²; р – удельное сопротивление материала проводов; l – длина ЛЭП, м; Р₂ – мощность потребителя, Вт; U₂ – напряжение на потребителе.

Выбранное по допустимой потере напряжения сечение проводов ЛЭП должно быть проверено по допустимому току.

Из выражения (2.36) видно, что сечение проводов зависит от напряжения на потребителе U₂. Так как эта зависимость квадратичная, то для уменьшения сечения проводов рационально увеличивать напряжение ЛЭП. В настоящее время напряжение ЛЭП переменного тока увеличено до 1150 кВ, постоянного тока до 1500 кВ.

КПД линии электропередачи определяется выражением:

, (2.37)

где Р₂ – мощность потребителя; Р₁ – мощность источника.

Как видно из формулы, чем больше потеря напряжения в проводах , тем меньше КПД линии электропередачи. КПД длинных линий электропередачи от 90 до 98%.

Параллельным соединением участков электрической цепи называют соединение, при котором все участки цепи присоединяются к одной паре узлов, т. е. находятся под действием одного и того же напряжения (рис. 2.12). Токи параллельно включенных участков обратно пропорциональны сопротивлениям этих участков.

При параллельном соединении потребителей с сопротивлениями

R₁, R₂и R₃токи потребителей равны:



Воспользовавшись первым законом Кирхгофа для рассматриваемой цепи, можно определить ток (I) в неразветвленной части цепи:

I = I₁ + I₂ + I₃ или

тогда

(2.38)

Т.е. обратная величина общего (эквивалентного) сопротивления (R) параллельно включенных потребителей равна сумме обратных величин сопротивлений этих потребителей.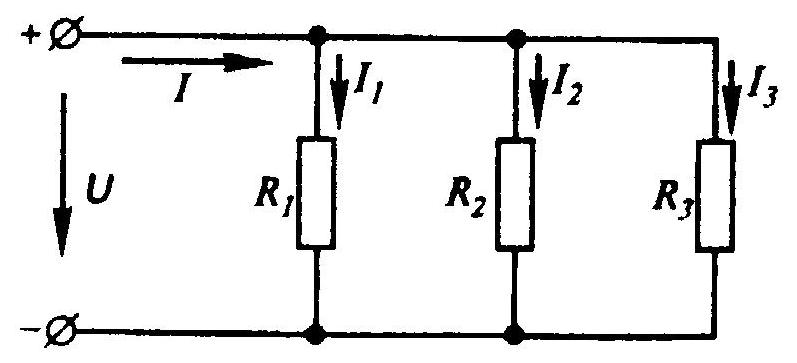



Рис. 2.12.

Величина обратная сопротивлению, определяет проводимость потребителя (g). Общая (эквивалентная) проводимость цепи при параллельном соединении потребителей определяется выражением:

(2.39)

Если параллельно включены n одинаковых потребителей с сопротивлением R' каждое, то эквивалентное сопротивление этих потребителей . Если параллельно включены два потребителя с сопротивлениями R₁ и R₂ , то общее (эквивалентное) их сопротивление по (2.6.6.):

(2.40)

Если параллельно включены три потребителя с сопротивлениями R₁, R₂и R₃, то общее их сопротивление (8.9):

(2.41)

Изменение сопротивления какого-либо из параллельно соединенных потребителей не влияет на режим работы (напряжение) всех потребителей, включая изменяемый. Поэтому параллельное соединение потребителей нашло широкое практическое применение.

При параллельном соединении потребителей на большем сопротивлении тратится меньшая мощность:



Вопросы для самопроверки

1. 
   Как формулируется первый закон Кирхгофа?
   
2. 
   Какими формулами описывается первый закон Кирхгофа?
   
3. 
   Дайте определение элементов электрической цепи.
   
4. 
   Как формулируется второй закон Кирхгофа?
   
5. 
   Какие параметры электрической цепи связывает второй закон Кирхгофа?
   
6. 
   Какими формулами определяются зависимости второго закона Кирхгофа?
   
7. 
   Может ли сопротивление участка двух параллельно соединенных проводников быть больше (меньше) любого из них? Объясните ответ.
   
8. 
   Какие законы сохранения используются для вывода формул сопротивления параллельного и последовательного соединения проводников?
   
9. 
   Проанализируйте аналогию между приводимыми здесь формулами и формулой для расчета сопротивления одного проводника через его геометрические параметры: . В чем заключается эта аналогия?
   
10. 
    Дайте определение электрической проводимости. Приведите формулы расчёта проводимости последовательного и параллельного участка цепи.
    

§2.7. Расчет электрических цепей постоянного тока.

Метод эквивалентных преобразований

В ряде случаев расчет сложной электрической цепи упрощается, если в ее схеме замещения заменить группу резистивных элементов другой эквивалентной группой, в которой резистивные элементы соединены иначе. Взаимная эквивалентность заключается в том, что после замены режим работы остальной части цепи не изменится.

А. Смешанное соединение резистивных элементов. При наличии в цепи одного источника внешнюю по отношению к нему часть схемы можно в большинстве случаев рассматривать как смешанное (последовательно - параллельное) соединение резистивных элементов.

Для расчета такой цепи удобно преобразовать ее схему замещения в эквивалентную схему с последовательным соединением резистивных элементов. Например, в цепи на рис. 1, а между узлами а и b включены три резистивных элемента с сопротивлениями r₂, r ₃ и r ₄, т.е. проводимостями

, , ;

эквивалентная проводимость:

,

После замены параллельного соединения резистивных элементов эквивалентным резистивным элементом с сопротивлением 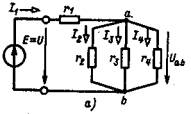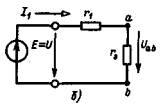получается эквивалентная схема с последовательным соединением двух резистивных элементов г₁, и r_э (рис. 1, б).



Рис. 2.13.

Ток в неразветвленной части



и токи в параллельных ветвях

где , , .

Б. Соединение резистивных элементов по схеме звезды и треугольника. В общем случае схему замещения цепи по схеме n-лучевой звезды из резистивных элементов можно заменить эквивалентной схемой в виде n-стороннего многоугольника. Обратное преобразование возможно в ограниченном числе случаев. В частности, преобразования в обоих направлениях возможны для случая треугольника и трехлучевой звезды.

Эквивалентность схем в виде треугольника и звезды (рис. 2.13) получается приравниванием значений сопротивлений или проводимостей между одноименными узлами этих схем, отсоединенных от остальной части цепи.

Найдем сопротивление между узлами А и В.

Проводимость между узлами А и В для схемы треугольника на рис. 2.13, а – g_AB.

Сопротивление между узлами А и В - величина, обратная проводимости между этими узлами, т. е.

R_AB = .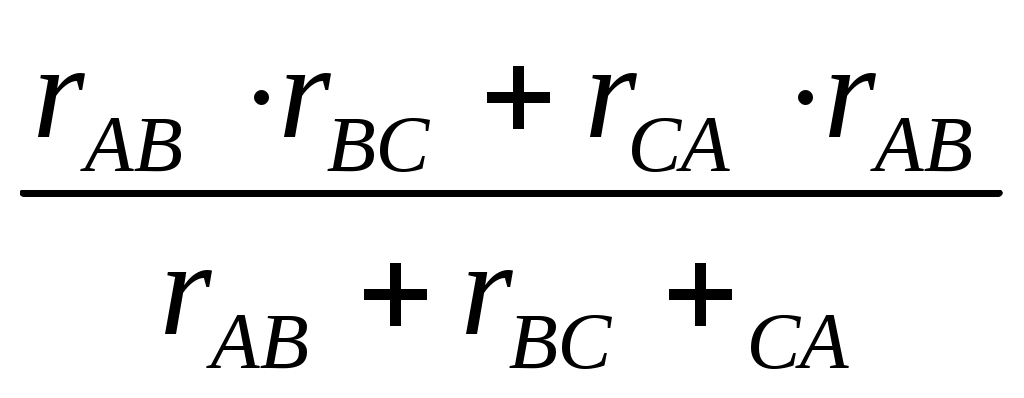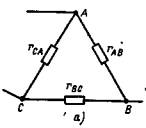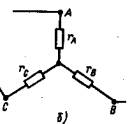



Рис. 2.14.

Для схемы звезда на рис. 2.13, б сопротивление между теми же узлами А и В равно сумме сопротивлений двух ветвей: r_A + r_B.

Если заданы сопротивления R₁₂, R₂₃, R₃₁ треугольника, то сопротивления каждого луча звезды определяются по формулам:







Наоборот, если заданы сопротивления R₁,R₂,R₃ звезды, то сопротивления каждой стороны треугольника определяются по формулам:







При совмещении треугольника и звезды сопротивлениилегко запомнить графическое правило для «звезды»:

сопротивление луча звезды равно произведению сопротивлений прилегающих сторон треугольника, деленному на сумму сопротивлений трех сторон треугольника

и правило для «треугольника»:

сопротивление стороны треугольника равно сумме сопротивлений прилегающих луней звезды и их произведения, разделенного на сопротивление третьего луча.

Метод контурных токов.

Для расчета сложных электрических цепей широко используют метод контурных токов, в основу которого положены расчетные (условные) контурные токи, замыкающиеся по смежным контурам разветвленных электрических цепей.

Метод контурных токов позволяет при составлении системы уравнений для расчета электрических цепей не записывать уравнения по первому закону Кирхгофа и тем самым уменьшить общее количество уравнений, необходимых для расчета. Истинные значения токов в ветвях электрической цепи определяются направлениями контурных токов. При этом  во всех замкнутых контурах для упрощения процесса расчета целесообразно задавать контурным токам одинаковые положительные направления. Число уравнений при расчете по методу контурных токов равно числу контурных токов.

При составлении контурных уравнений по второму закону Кирхгофа для замкнутых контуров ЭДС источников питания принимаются положительными, если их направления совпадают с направлениями контурных токов, при несовпадении с контурным током их записывают со знаком « – ». Со знаком « – » записывают напряжения, а также падения напряжений, направленные против контурного тока, а со знаком « + », если они совпадают с ним.

При этом величины контурных токов во внешних (не смежных) ветвях оказываются равными по значению токам в ветвях, которые нанесены на электрическую схему. Токи смежных ветвей равны разности контурных токов соседних контуров. Со знаком « + » записывается контурный ток, совпадающий с направлением тока в смежной ветви.

Применительно к электрической цепи (рис. 2.18) в соответствии с заданным направлением ЭДС, напряжения, токов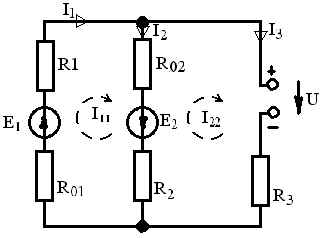



Рис. 2.18.

в ветвях и контурных токов уравнения, составленные по второму закону Кирхгофа для замкнутых контуров, записывают в следующем виде:

E₁+E₂ = (R₀₁+R₀₂+R₁+R₂)•I₁₁ – (R₀₂+R₂)•I_22.

–E2 = ( R₀₂+R₂+R₃)I22 – (R₀₂+R₂)•I₁₁+U

В результате решения полученной системы уравнений определяют контурные токи I₁₁ и I₂₂. При этом токи во внешних (несмежных) ветвях электрической цепи оказываются численно равными соответствующим контурным токам: I₁=I₁₁, I₃=I₂₂.

Ток в смежной ветви определяют из уравнения, составленного по первому закону Кирхгофа для точки разветвления электрической цепи: I₁ – I₂ – I₃=0, откуда I₂=I₁ – I₃=I₁₁ – I₂₂.

Расчёт электрических цепей постоянного тока методом контурных токов.

Пример 1. Определить токи в цепи. Самостоятельно выбрать направления токов и найти их численное значение. Указать, возможно ли реальное существование цепи с такими характеристиками. Обосновать свой ответ.

Дано: 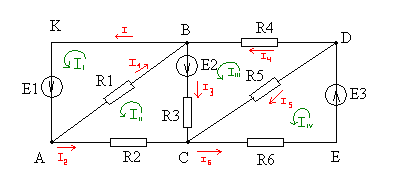Определить:



Решение:

1. Выбираем направление токов в цепи через каждое сопротивление. Численное значение токов определим методом контурных токов.

Выделим четыре независимых контура с токами

Токи внешних ветвей равны контурным токам:



Остальные токи определяем через соответствующие контурные токи.

2. Составляем систему уравнений: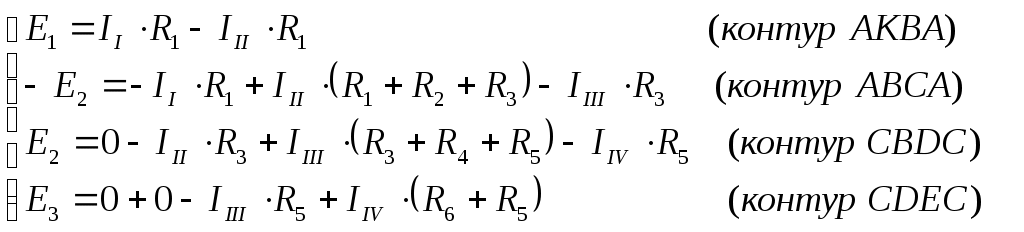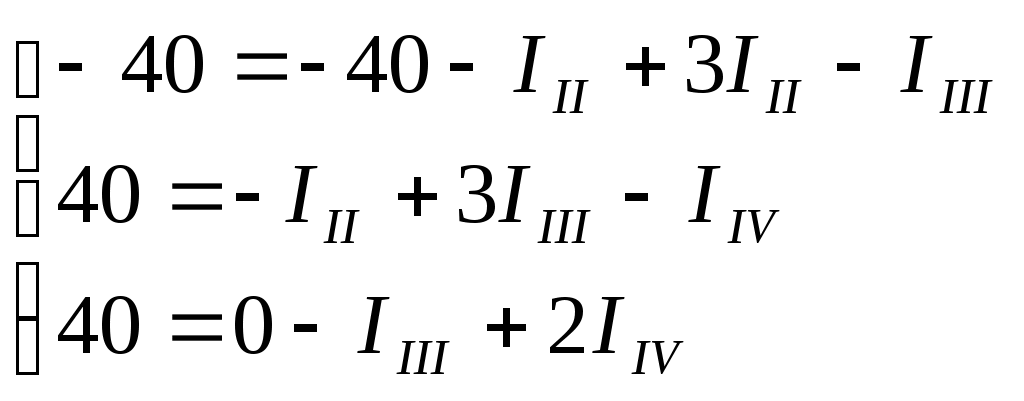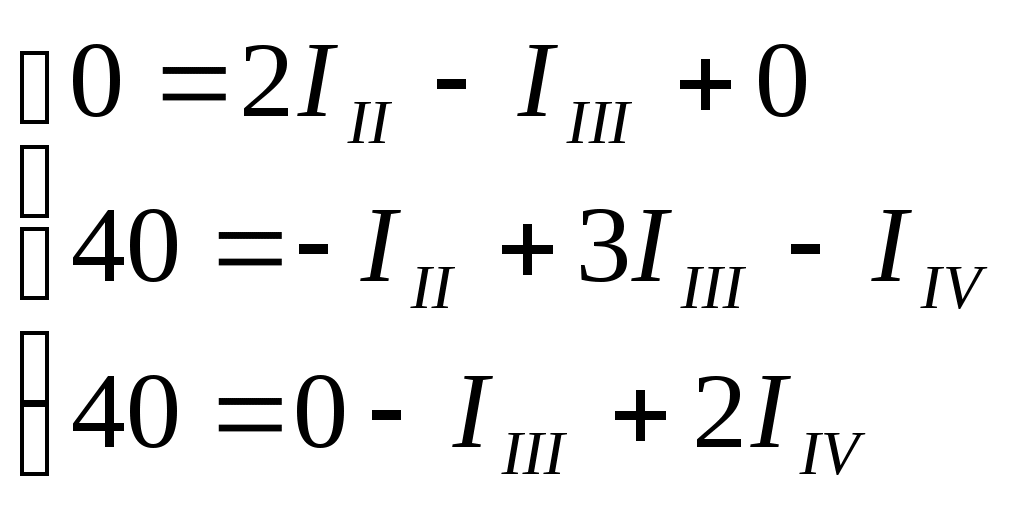









3. Определитель системы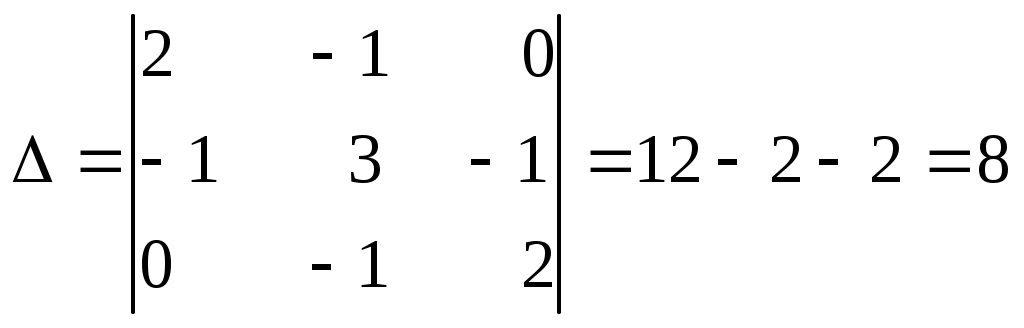



4. Определяем контурные токи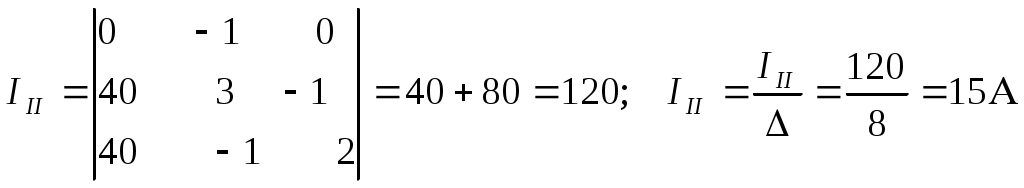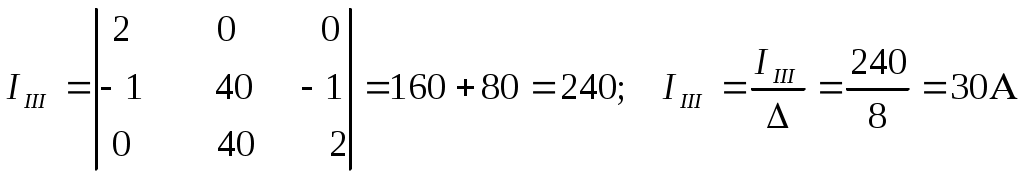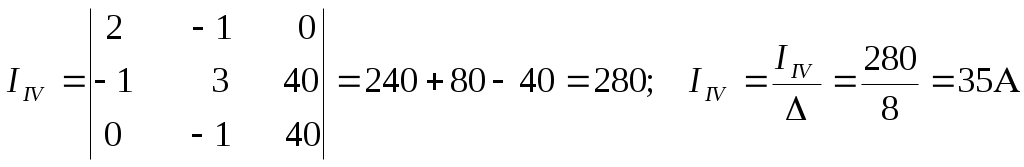





5. Определяем токи ветвей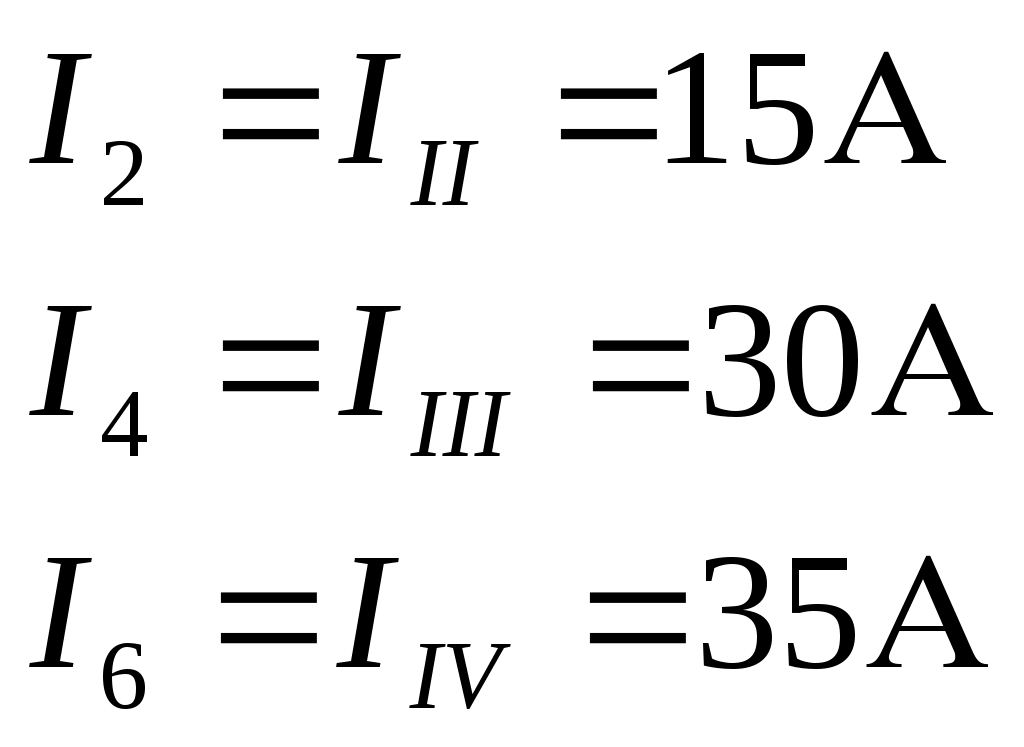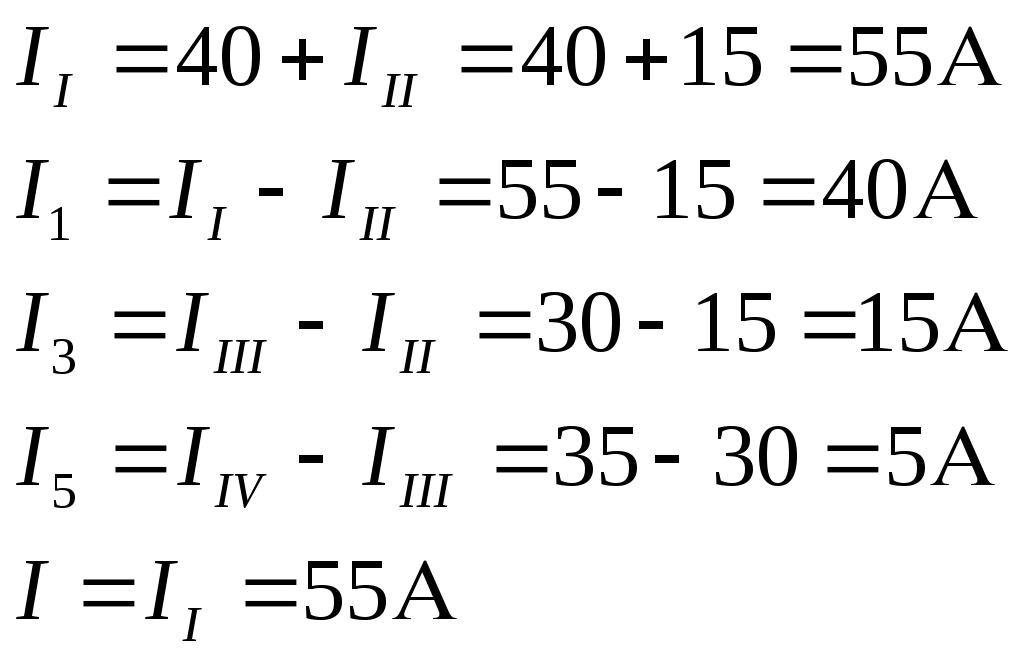





6. Проверяем решение по первому закону Кирхгофа для каждого узла.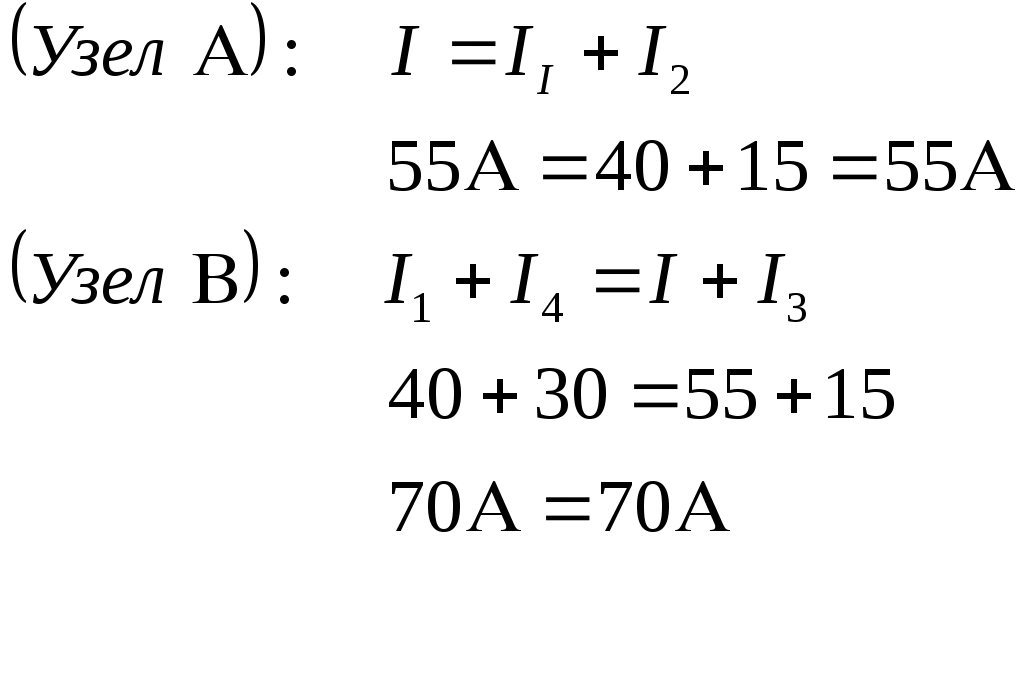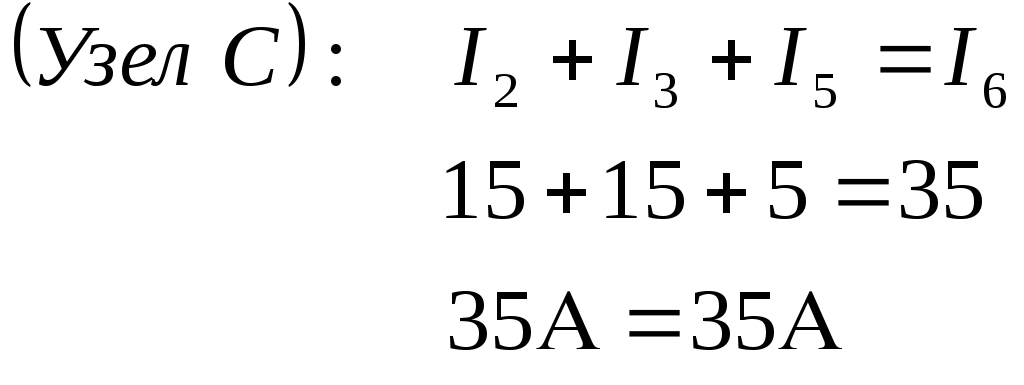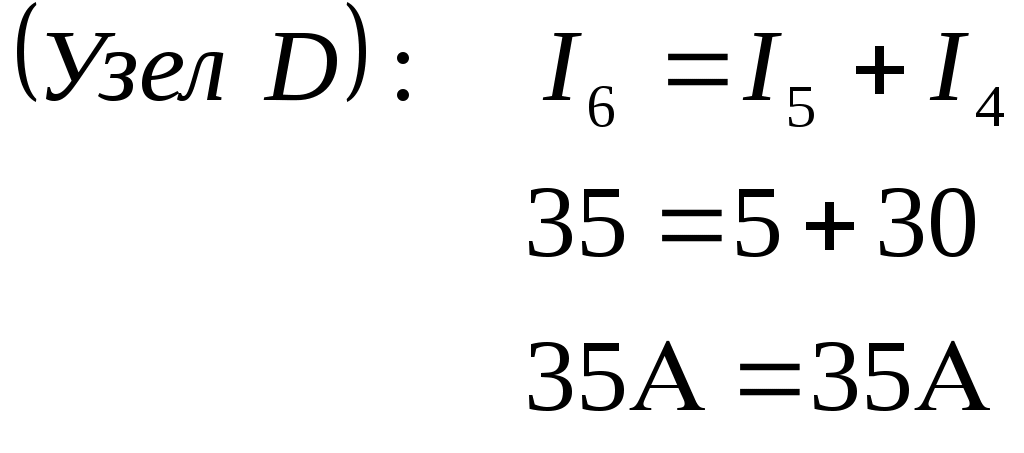







7. Реально существовать цепи с такими характеристиками не могут, так как источники тока обязательно обладают внутренним сопротивлением.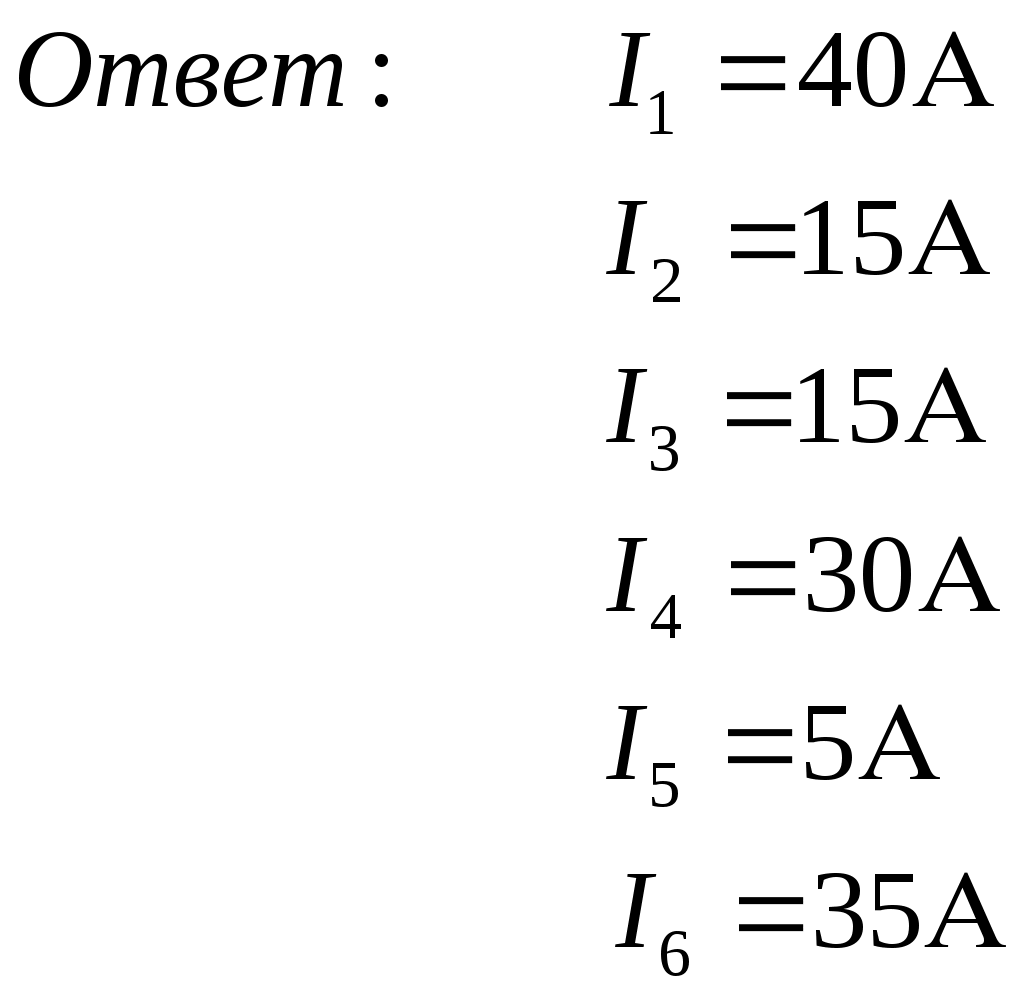



Задача. (выполнить самостоятельно) Определить общий ток I и токи I₁ – I₅ в ветвях электрической цепи постоянного тока (рис. 18). ЭДС источников питания: E₁=32 B, E₂=120 B, E₃=10 B, внутреннее сопротивление источника E1: R₀ = 2 Ом (внутренним сопротивлением других источников пренебречь). Сопротивление резисторов: R₁ = 10 Ом, R₂ = 4 Ом, R₃ = 6 Ом, R₄=5 Ом, R₅ = 8 Ом.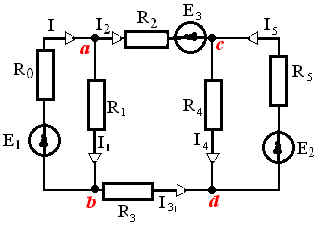



Рис. 2.19.
Задача. (выполнить самостоятельно) Электрическая цепь постоянного тока (рис. 20) содержит источники питания: E₁ = 50 B, E₂ = 20 B, E₃ = 45 B и резисторы с сопротивлением: R₁ = 10 Ом, R₂ = 30 Ом, R₃ = 50 Ом, R₄ = 20 Ом, R₅ = 1 Ом, R₆ =20 Ом, R₇ = 10 Ом. Напряжение, приложенное к цепи U = 80 В. Внутренние сопротивления источников R₀ = 0. Определить токи I₁ – I₆ в ветвях электрической цепи и напряжение U₁₄, действующее между точками 1 и 4 цепи.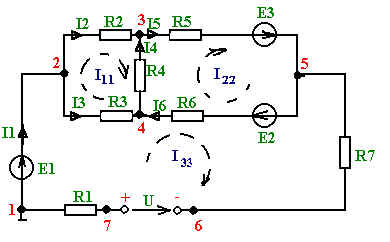



Рис. 2.20.

Метод узлового напряжения.

Используется для расчета электрических цепей, содержащих несколько параллельных ветвей, присоединенных к паре узлов. Определение узлового напряжения позволяет достаточно просто определять токи в параллельных ветвях и другие величины, характеризующие подобные цепи.

Узловое напряжение между двумя узлами определяют по выражению: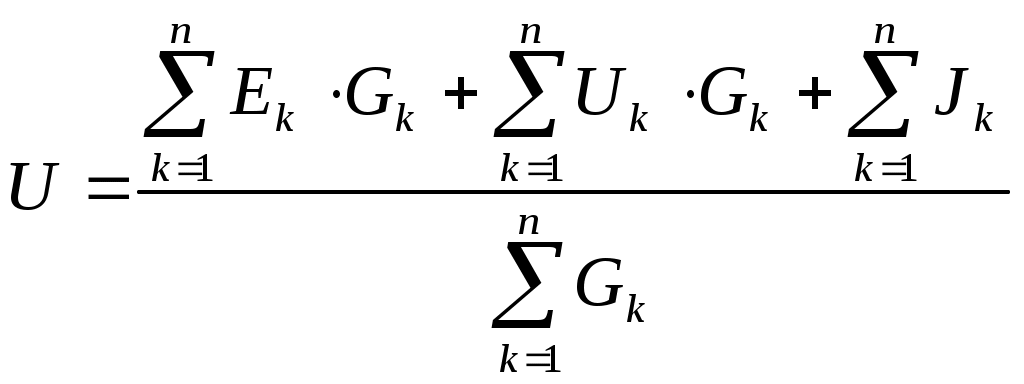

, где

– алгебраическая сумма произведений ЭДС на проводимости соответствующих ветвей;

– алгебраическая сумма произведений напряжений на проводимости соответствующих ветвей;

– алгебраическая сумма токов источников токов в ветвях;

– сумма проводимостей всех ветвей.

Алгоритм расчета цепей по методу узлового напряжения в цепи с источниками тока:

• 
  определить проводимости всех ветвей, выбрав условные положительные направления токов в ветвях;
  
• 
  задать положительное направление указанного напряжения, рассчитывая его по соответствующей формуле;
  
• 
  выбрать направления обходов контуров и составить уравнения по второму закону Кирхгофа, затем (при необходимости) – по первому закону Кирхгофа.
  

Значения ЭДС, напряжения и токи источников тока положительны, если они направлены по направлению обхода контура, и наоборот.

Алгоритм расчета цепей по методу узлового напряжения в цепи без источников тока упрощается, т.к. выражение для определения узлового напряжения приводится к виду: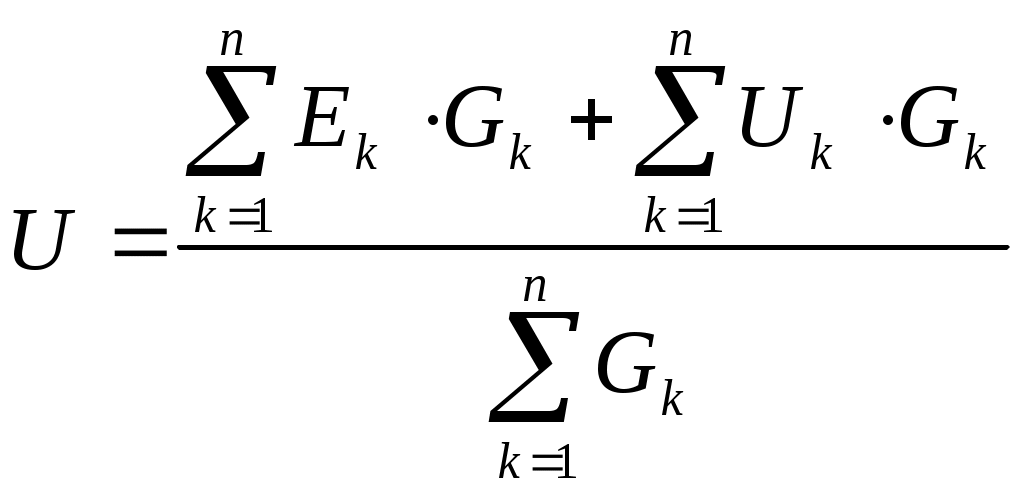



Пример 2. Два источника постоянного тока с ЭДС E₁=E₂=115 B и внутренними сопротивлениями R₀₁=0,2 Ом и R₀₂=0,4 Ом включены параллельно на нагрузку R_н=5 Ом (рис. 21). Определить токи I, I₁, I₂ в ветвях электрической цепи.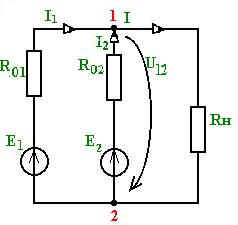



Рис. 2.21.

Решение:

Вычислим проводимости ветвей цепи:

G₁=1/R₀₁=1/0,2=5 См; G_н=1/R_н=1/5=0,2 См; G₂=1/R₀₂=1/0,4=2,5 См.

Тогда узловое напряжение, действующее между узлами 1 и 2 цепи:

= 112,0 В

Положительные направления токов в ветвях показаны на рис.1. По второму закону Кирхгофа для ветви с ЭДС E₁ получаем:

U₁₂+R₀₁ I₁=E₁, откуда

= (E₁ – U₁₂)•G₁ =(115 – 112)•5= 15 A.

Аналогично для ветви с ЭДС E₂:

= (E₂ – U₁₂)•G₂ =(115 – 112)•2,5= 7,5 A.

Ток для резистора R_н найдем по закону Ома:

I = U₁₂/R_н = 112/5 = 22,4 А.

Ответ: I₁ =15 A, I₂ = 7,5 A, I = 22,4 А.
Задача: (выполнить самостоятельно)

ЭДС аккумуляторной батареи E₁ = 8 B, ЭДС источника питания E₂ = 10 B, его внутреннее сопротивление R₀₂ = 0,5 Ом, сопротивление резистора

R₁ = 0,5 Ом, R_н = 5 В. Определить токи в ветвях в цепи постоянного тока.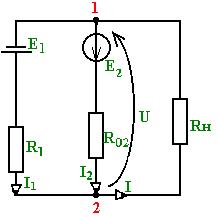



Рис. 2.22.

Метод наложения токов (метод суперпозиции).

Применяется для расчета электрических цепей с несколькими источниками тока. Удобен в случаях, когда не нужен полный расчет цепи, а достаточно определить токи на участках с источниками питания.

Заключается в том, что в каждой из ветвей электрической цепи ток определяется как алгебраическая сумма токов, вызываемых в ней воздействием каждого из источников. Рассматриваемая цепь с несколькими источниками ЭДС и напряжений заменяется расчетными цепями с одним источником, число которых равно числу источников, действующих в исходной цепи. В результате определяются частичные токи от действия данного источника. Значение действительных токов определяются как алгебраическая сумма частичных токов в этих ветвях.

Пример 3. Определить ток I в электрической цепи постоянного тока (рисунок 23). Сопротивление резистора R = 4 Ом, ЭДС Е₁ = 36 В, R₀₁ = 0,3 Ом ЭДС аккумуляторной батареи E₂ = 12 В, ее внутреннее сопротивление R₀₂ = 0,01 Ом.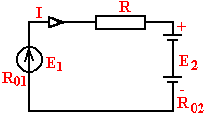



Рис. 2. 23.

Решение:

Ток в цепи при ЭДС E₂=0 (рис. а) по закону Ома для всей цепи: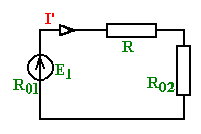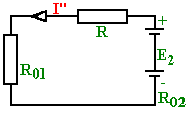

А



а). б).

Рис. 2.24.

Ток в цепи при ЭДС E₁ = 0 (рис. б):

А.

Ток в цепи при ЭДС E₂ = 0 (рис. а) по закону Ома для всей цепи:

Ток при наличии обоих источников питания:

I =I′-I″=8,35 – 2,78 = 5,57 A.

Ответ: I = 5,57 A.

Задача: (выполнить самостоятельно)

Два источника постоянного тока с ЭДС E₁ = 8 В, E₂ = 10 B и внутренними сопротивлениями R₀₁ = 0,6 Ом и R₀₂ = 0,5 Ом включены параллельно на нагрузку R_н = 2 Ом (рис. 25). Определить общий ток I в цепи, токи I₁ и I₂ в ветвях. (Ответ: I = 4,15 А, I₁ = 0,15 А, I₂ = 4А.)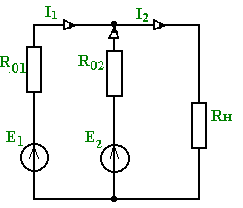



Рис. 2.25.