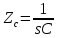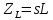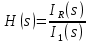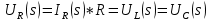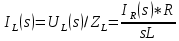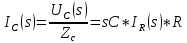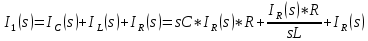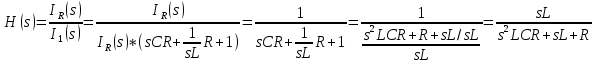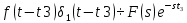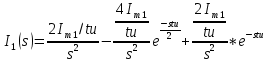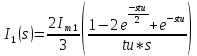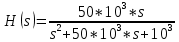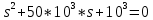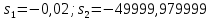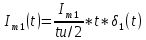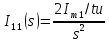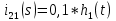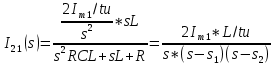курсач по тоэ. Анализ и моделирование переходных процессов в
 Скачать 46.13 Kb. Скачать 46.13 Kb.
|
|
МИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА) Факультет измерительных и биотехнических систем Кафедра теоретических основ электротехники КУРСОВАЯ РАБОТАпо дисциплине «Теоретические основы электротехники» Тема: АНАЛИЗ И МОДЕЛИРОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНОЙ ЦЕПИ ПРИ ВОЗДЕЙСТВИИ СИГНАЛОВ ПРОИЗВОЛЬНОЙ ФОРМЫ ВАРИАНТ №14
Санкт-Петербург 2022 ЗАДАНИЕ НА КУРСОВУЮ РАБОТУСтудент(ка) Мамыкова Виолетта Данияровна Группа 0586 Тема работы: Анализ и моделирование переходных процессов в линейной цепи при воздействии сигналов произвольной формы Исходные данные: 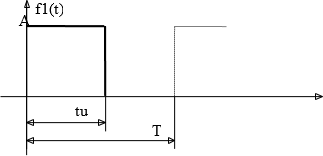 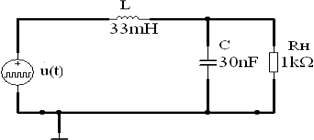 Рис. 1. Импульснапряженияf1(t) Рис. 2. Схема электрическойцепи 𝑈𝑚 = 10 В 𝑡и = 0.5 мс 𝑇 = 1 мс Содержание пояснительной записки: «Аннотация», «Содержание», «Введение», «Заключение», «Список использованных источников», «Анализ электрической цепи» Предполагаемый объём пояснительной записки: Не менее 5 страниц. Дата выдачи задания: 10.02.2022 Дата сдачи реферата: 07.04.2022 Дата защиты реферата: 12.04.2022
АННОТАЦИЯЦелью данной курсовой работы является расчёт и анализ переходных процессов при воздействии произвольной формы. Используется цепь второго порядка с RLC-элементами. Требуется найти выходную реакцию и произвести спектральный анализ схемы. Используются различные методы для нахождения выходной реакции: численный метод переменных состояния, операторный метод, а также аппроксимация сигналов в ходе гармонического анализа. На этих этапах применяется система MathCAD. Моделирование схемы в MultiSim отображает осциллограмму выходной реакции. Результатом исследования стал полученный разными способами график выходной реакции, который имеет одинаковый вид во всех разделах курсовой работы, а также оценка искажений входного сигнала. SUMMARYThe purpose of this course work is the calculation and analysis of transients under the influence of an arbitrary shape. A second-order chain with RLC elements is used. It is required to find the output reaction and perform a spectral analysis of the circuit. Various methods are used to find the output reaction: the numerical method of state variables, the operator method, as well as the approximation of signals during harmonic analysis. At these stages, the MathCAD system is used. The simulation of the circuit in MultiSim displays an oscillogram of the output reaction. The result of the study is a graph of the output reaction obtained in different ways, which has the same appearance in all sections of the course work, and an assessment of input signal distortion. СОДЕРЖАНИЕВведение 5 Численный метод переменных состояния 6 Составление дифференциальных уравнений состояния цепи 6 Расчёт реакции на выходе методом Рунге-Кутта 7 Операторный метод 8 Определение функции передачи цепи 8 Расчёт реакции через обратное преобразование Лапласа 10 Спектральный анализ 11 Построение частотных характеристик 11 Гармонический анализ 15 Входное воздействие 15 Выходная реакция 16 Моделирование переходного процесса в цепи 18 Заключение 21 Список использованных источников 22 ВВЕДЕНИЕОбъектом исследования являются различные методы определения реакции на выходе электрической цепи при воздействии произвольной формы и её анализ. Для этого используется электрическая цепь с двумя накопительными элементами и источником напряжения произвольной формы. Элементы в цепи изменяют вид реакции. Для начала следует записать воздействие в аналитическом виде с помощью ступенчатых дельта-функций и найти реакцию, руководствуясь изученными методами расчёта цепей. Схема достаточно простая, чтобы использовать уравнения Кирхгофа, однако её расчёт усложняет наличие двух накопительных элементов. Поэтому, наряду с численным методом переменных состояния, используется операторный метод. Переход в операторную область обусловлен не только необходимостью рассчитать точную реакцию на выходе. Благодаря получению передаточной функции цепи, можно анализировать искажения, вносимые цепью в изначальное воздействие. Мы руководствуемся двумя критериями оценки ширины спектра воздействия: критерий первого лепестка и амплитудный критерий. Таким образом, мы сравниваем ширину спектра с полосой пропускания, которую получаем из передаточной функции. В основе этой оценки лежит предположение, что на определённом уровне спектр обладает наибольшей мощностью, передача которой не вносит значимых искажений. Используется и гармонический анализ – разложение воздействия и реакции на сумму гармонических функций. Определяется их амплитудный и фазовый дискретный спектры, с помощью которых в итоге можно изобразить аппроксимацию. Использование рядов Фурье не даёт большой точности: для получения идентичных изображений в аппроксимации, теоретически, необходимо найти бесконечное число слагаемых, что невозможно сделать. Поэтому достаточно найти 5-6 слагаемых для приемлемой точности. Чтобы завершить работу и убедиться в правильности расчётов реакции, необходимо обратиться к специальному программному обеспечению, которое позволяет построить электрическую цепь и увидеть изображение сигнала на различных элементах. Одним из таких ПО является MultiSim, который используется в электронике для расчёта сложных цепей. ЧИСЛЕННЫЙ МЕТОД ПЕРЕМЕННЫХ СОСТОЯНИЯСоставление дифференциальных уравнений состояния цепиАналитический вид временной функции воздействия f1(t) (рис. 1): 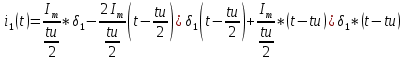 Система дифференциальных уравнений состояния цепи: КАРТИНКА'>КАРТИНКА 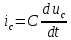 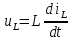 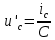 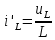 ЗНК: 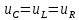 ЗТК: 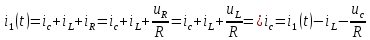 Уравнения состояния: 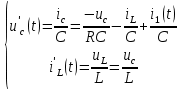 Определим вынужденные составляющие для проверки системы: КАРТИНКА Проверка: 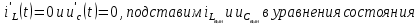 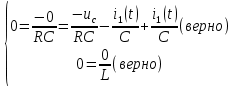 Расчёт реакции на выходе методом Рунге-КуттаСоставляются матрицы коэффициентов. В дальнейшем используется функция Rkfixed для решения систем однородных дифференциальных уравнений методом Рунге-Кутта с постоянным шагом. Используется 1000 точек для построения графиков:
|

 ОПЕРАТОРНЫЙ
ОПЕРАТОРНЫЙ