|
|
моделирование системы интеграции. Анализ исходных данных 5 Анализ процесса резания как объекта управления 8 Разработка структурной схемы сар 10 Основной контур системы 14 14 Рисунок
Оглавление Введение 4Анализ исходных данных 5Анализ процесса резания как объекта управления 8Разработка структурной схемы САР 10Основной контур системы 14 14Рисунок 6. Основной контур системы 14 15 16Рисунок 8.основной контур системы с подачей возмущений. 16 16Рисунок 9. Переходный процесс замкнутой САР при максимальном скачке возмущения. 16Обоснование необходимости применения адаптивного управления 17Рисунок10. Переходной процесс при изменении Кпр в 3 раза. 18Рисунок11. работа классической системы при пульсирующем изменении Кпр. 19Выбор класса адаптивной системы управления, функциональная схема 20Разработка структурной схемы адаптивной системы управления, расчет элементов контура адаптации 21Выводы о качестве работы АдСУ по результатам моделирования 24Заключение 27Список литературы 28
Введение
В последние десятилетия возникла необходимость осуществлять автоматическое управление объектами, параметры которых в результате изменений во внешней среде также изменяются в широком диапазоне. К такого рода объектам прежде всего относятся промышленные объекты, работающие на сырье с сильными случайными колебаниями параметров, летающие объекты – самолеты и ракеты, проникающие в верхние слои атмосферы. Параметры и структура систем управления могут меняться непредвиденным образом в процессе функционирования системы управления, характер возмущающих воздействий, принятых при расчете может не соответствовать их действительным характеристикам. Все это на практике приводит к расстройке системы, отклонению от расчетных режимов работы, снижению качества управления и даже к потере устойчивости.
В последнее время установилось более или менее общепризнанное представление об одном из наиболее разработанных и распространенных в практике классе адаптивных систем, получивших название самонастраивающихся (СНС), разработка одной из которых является основной целью данной курсовой работы.
Анализ исходных данных
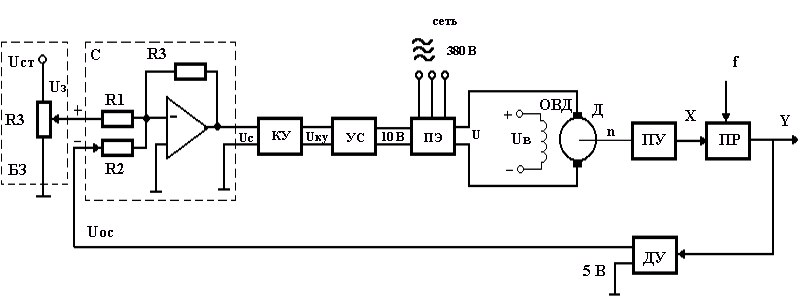
Схема системы автоматического регулирования (САР) выходной координаты Y приведена на рис. 1:
Рисунок 1. Схема системы автоматического регулирования (САР) выходной
координаты.
САР регулирует выходную координату процесса резания металла с заданной точностью. Каждый процесс резания характеризуется своей выходной координатой, которая на функциональной схеме обозначена буквой Y. Процесс резания на схеме (рис.1) обозначен функциональным блоком ПР, управляющей координатой ПР является глубина резания S (на схеме обозначена Х), возмущающим воздействием является подача t и скорость резания V (на схеме обозначены буквой f).
ПУ – передаточное устройство, это механическая система, преобразующая механическую энергию вала двигателя в механическую энергию управляющего воздействия процесса резания. ПУ является линейным звеном. С точки зрения динамики является апериодическим звеном первого порядка с постоянной времени 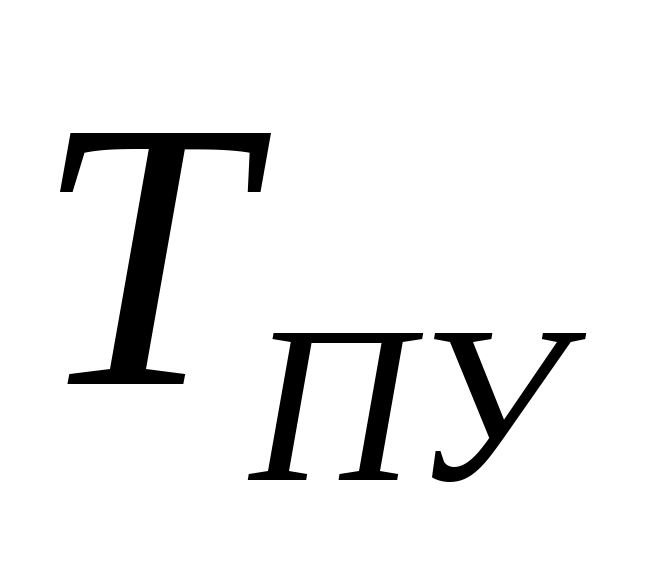 . Двигатель Д преобразует электрическую энергию в механическую энергию вращения вала. Двигатель является машиной постоянного тока с независимым возбуждением. Возбуждение машины осуществляется обмоткой ОВД. Поток возбуждения в процессе регулирования не изменяется и остается равным его номинальному значению. Регулирование скорости nд двигателя осуществляется изменением напряжения якоря U. . Двигатель Д преобразует электрическую энергию в механическую энергию вращения вала. Двигатель является машиной постоянного тока с независимым возбуждением. Возбуждение машины осуществляется обмоткой ОВД. Поток возбуждения в процессе регулирования не изменяется и остается равным его номинальному значению. Регулирование скорости nд двигателя осуществляется изменением напряжения якоря U.
ПЭ – преобразователь электрической энергии, преобразует электрическую энергию промышленной сети трехфазного переменного тока в электрическую энергию постоянного тока и регулирует величину выходного напряжения U, питающего цепь якоря двигателя Д. Преобразователь электрической энергии является линейным звеном. Выходное напряжение U равно номинальному значению при напряжении управления 10 В. С точки зрения динамики процесса ПЭ представляет собой апериодическое звено второго порядка с постоянными времени 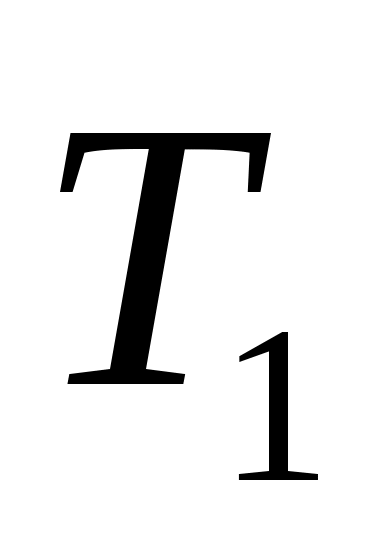 и и 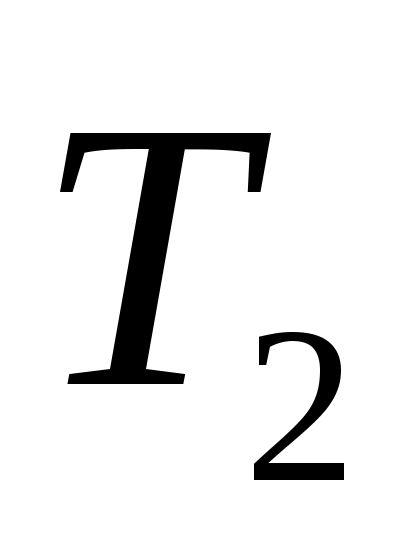 . .
УС – усилитель. Является безынерционным звеном, усиливает напряжение, поступающее от корректирующего устройства.
КУ – корректирующее устройство. Корректирует динамические свойства САР. Статический коэффициент передачи КУ равен единице.
БЗ – блок задания. Блоком задания задается напряжение 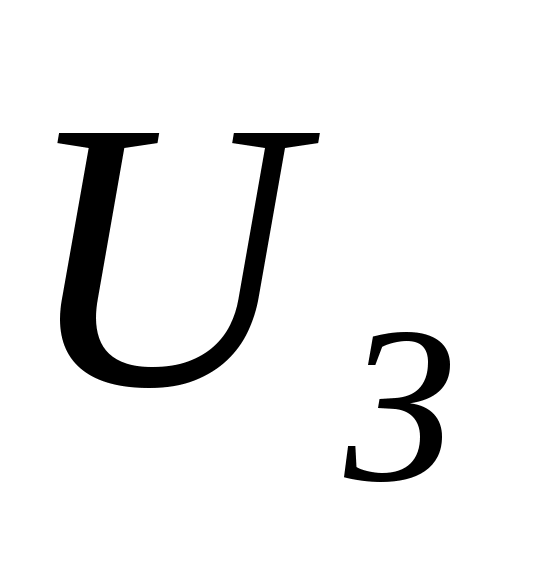 , его величина определяет величину задания выходной координаты САР. БЗ содержит в себе источник стабилизированного напряжения , его величина определяет величину задания выходной координаты САР. БЗ содержит в себе источник стабилизированного напряжения 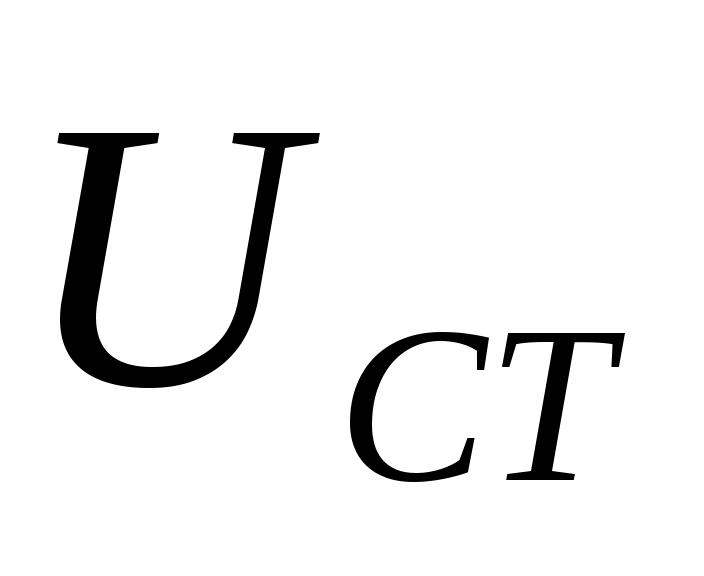 и резистор R3. и резистор R3. 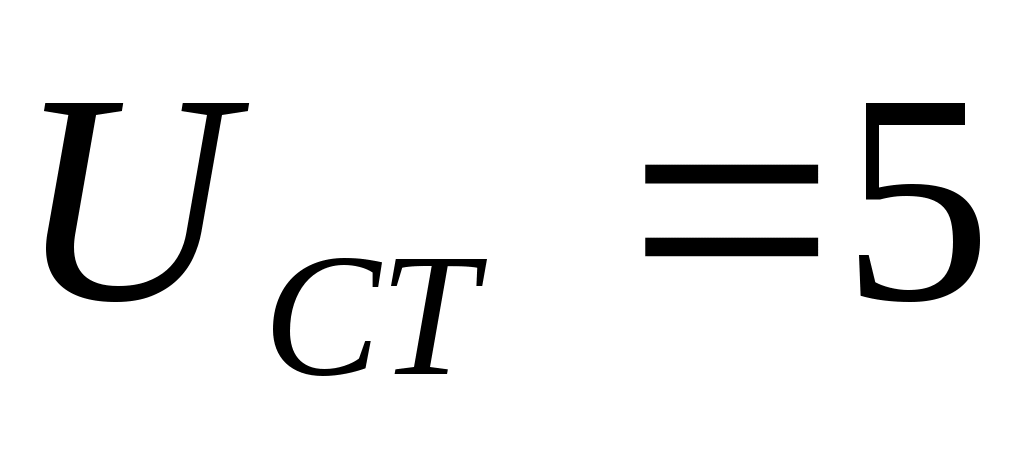 В. В.
ДУ – измерительная система выходной координаты процесса резания. Представляет собой с точки зрения динамики апериодическое звено первого порядка с постоянной времени 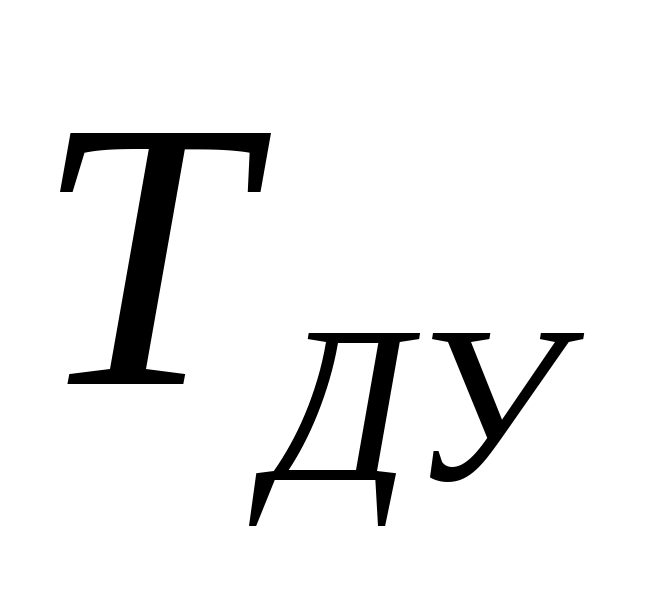 . При номинальном значении выходной координаты выдаёт напряжение . При номинальном значении выходной координаты выдаёт напряжение 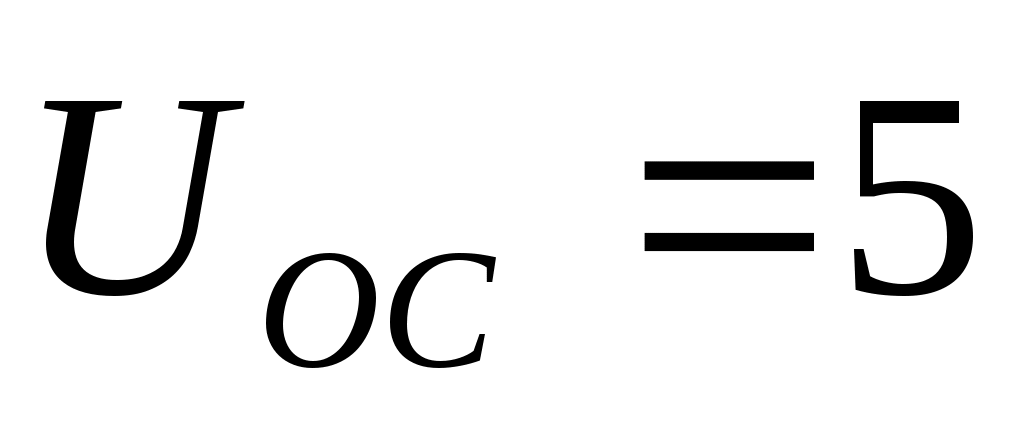 В. В.
С – сумматор на базе операционного усилителя и на резисторах R1, R2, R3. Является безынерционным звеном с коэффициентом передачи равным единице. На резистор R1 сумматора поступает положительное напряжение U3 с блока задания. На резистор R2 поступает напряжение обратной связи UОС с отрицательным знаком. Просуммированное напряжение поступает с сумматора на КУ. Суммирование осуществляется по алгоритму 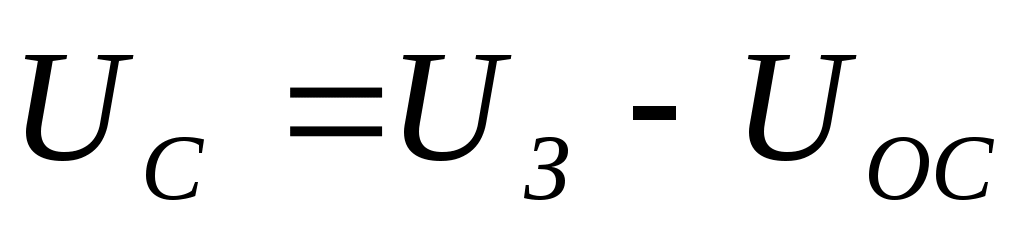 . .
Функциональная схема САР представлена на рис.2:
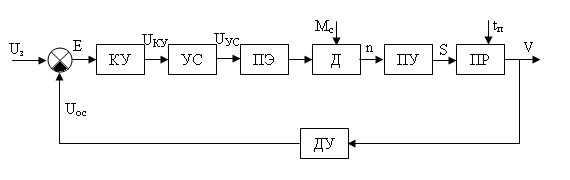
Рисунок 2. Функциональная схема САР.
По алгоритму функционирования данная САР является следящей. В ней выходная величина – скорость – регулируется с заданной точностью при изменении напряжения на входе, т.е. система управляет выходной координатой. На вход системы подается напряжение 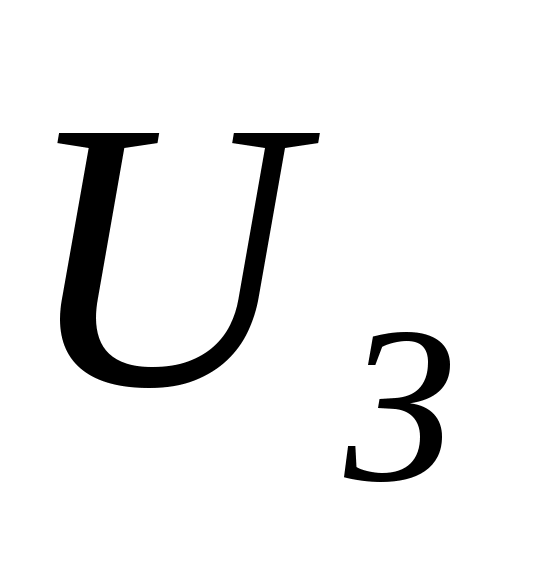 , соответствующее заданной скорости резания. Это напряжение сравнивается с напряжением , соответствующее заданной скорости резания. Это напряжение сравнивается с напряжением 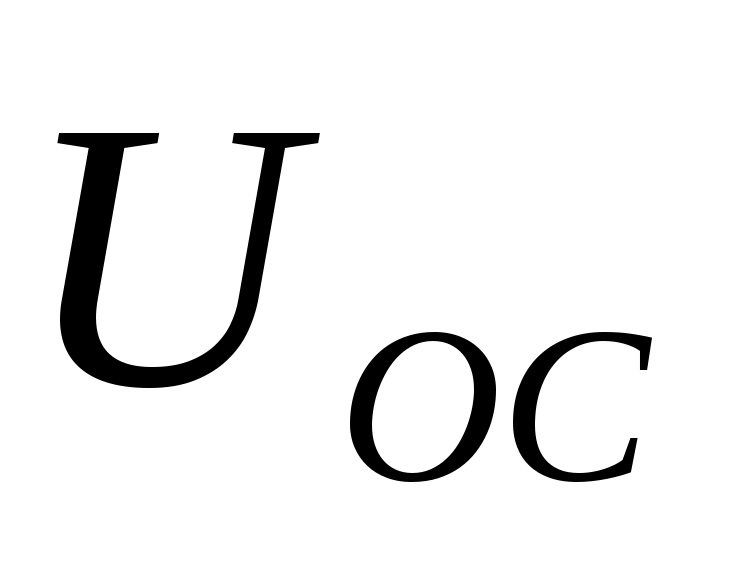 , поступающим с датчика обратной связи – например, естественной термопары. Если существует ненулевая разница этих напряжений – ошибка регулирования , поступающим с датчика обратной связи – например, естественной термопары. Если существует ненулевая разница этих напряжений – ошибка регулирования 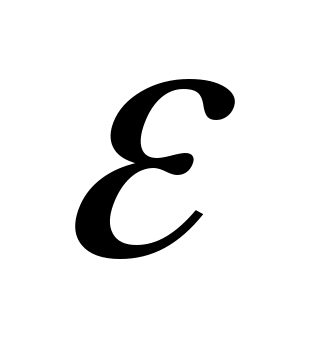 , то она с соответствующим знаком поступает на КУ, УС, ПЭ. ПЭ таким образом меняет напряжение на своем выходе, чтобы свести ошибку регулирования путем изменения скорости вращения двигателя к минимуму или нулю. Если на систему действуют возмущения, то система с обратной связью будет компенсировать эти возмущения, поддерживая температуру в области резания постоянной. , то она с соответствующим знаком поступает на КУ, УС, ПЭ. ПЭ таким образом меняет напряжение на своем выходе, чтобы свести ошибку регулирования путем изменения скорости вращения двигателя к минимуму или нулю. Если на систему действуют возмущения, то система с обратной связью будет компенсировать эти возмущения, поддерживая температуру в области резания постоянной.
Анализ процесса резания как объекта управления
1. Определение состава выходных координат ПР. В качестве выходных координат можно взять температуру в зоне резания, параметры стружки, силу резания, уровень шероховатости обработанной поверхности, скорость резания и др.
2. Выбор выходной координаты, наиболее эффективно действующей на процесс резания. За выходную координату возьмём скорость резания, будем стремиться поддерживать ее на уровне оптимальной, которой соответствует минимальный износ инструмента, максимальное качество процесса резания и др.
3. Математическое описание ОУ: уравнение (1) отражает влияние на оптимальную скорость различных факторов.
ОУ описывается следующим уравнением:
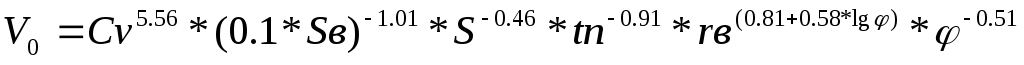 (1) (1)
4. Определение ограничений, в условии которых должен действовать ПР.
Температура в зоне резания не должна превышать 800 С, чтобы не плавился резец. Также рекомендуется работать в той зоне скоростей (температур), где не образуется нарост на вершине режущего инструмента.
5. Определение состава управляющих координат(УК). На выходную координату оказывают влияние глубина резания tр, подача S, радиус вершины.
6. Выбор управляющей координаты , оказывающей самое эффективное воздействие на выходную координату. Из уравнения (1) видно, что подача наиболее эффективно влияет на скорость резания. Кроме того, изменять подачу металлорежущего станка несложно. Поэтому выберем в качестве управляющей координаты подачу S.
7. Определение состава возмущений. По условию, на ПР в качестве возмущения действует изменение величины снимаемого припуска, твердость инструмента, величина износа задней поверхности инструмента.
8. Определение диапазона изменения возмущений
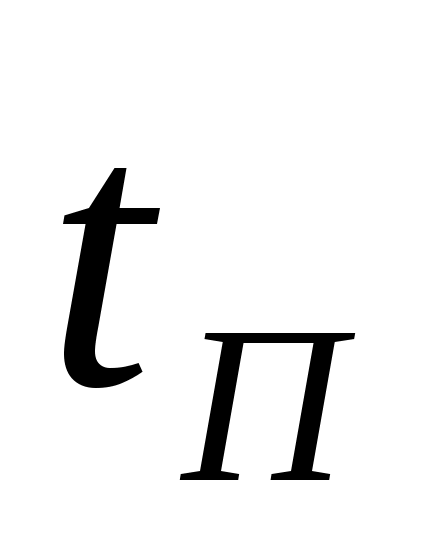 изменяется в пределах от 0,5 до 0,7 мм, т.е.Δ изменяется в пределах от 0,5 до 0,7 мм, т.е.Δ 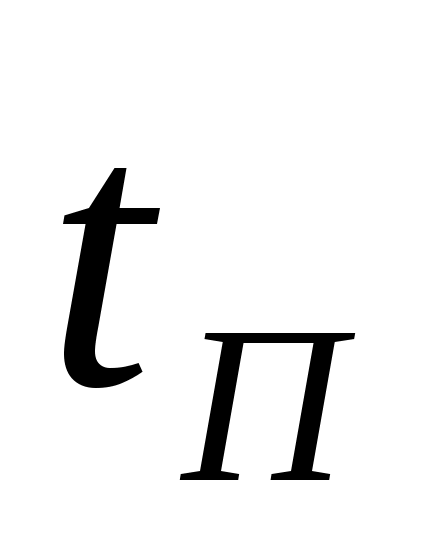 =0,2мм. =0,2мм.
Учитывая вышесказанное, ПР в качестве объекта управления можно представить в упрощенном виде следующим образом:
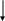 ∆tп ∆tп

  S Процесс резания V S Процесс резания V
Рисунок 3. Функциональная схема процесса резания как объекта управления.
9. Определение отклонения выходной координаты при совместном действии возмущений: скорость резания будет изменяться в пределах
(Sв при температуре 680 составляет 710 МПа)
V0мин= 105.56•(0,1•920•106)-1.01•(0,21•10-3)-0.46•(0,5•10-3)-0.91•(0,5•10-3) (0.81+0,58•lg45)•
45-0.51=44 м/мин
V0макс=105.56•(0,1•920•106)-1.01•(0,21•10-3)-0.46•(0,7•10-3)-0.91•(0,5•10-3) (0.81+0,58•lg45)•
45-0.51=59,8 м/мин
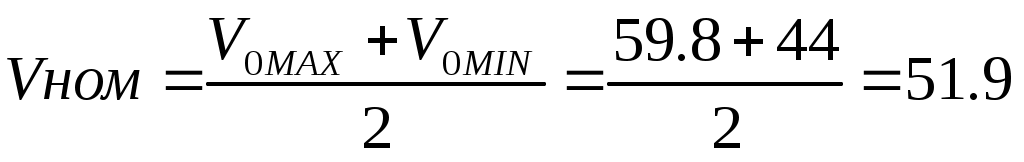 м/мин м/мин
0тклонение выходной координаты получилось равным
Сравнение точности с заданной:
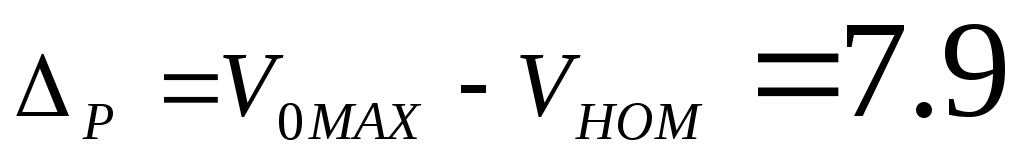
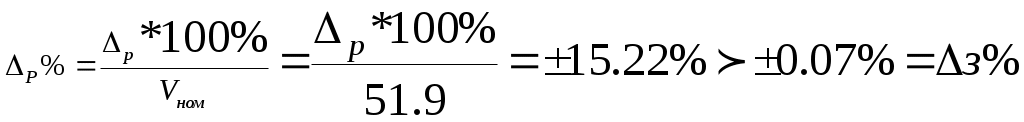
Реальное отклонение выходной координаты больше допустимого .
Разработка структурной схемы САР
Структурную схему составим на основании функциональной схемы на рис. 2. Структурная схема неизменяемой части САР будет включать в себя все элементы САР, кроме корректирующих устройств.
Преобразователь энергии. С точки зрения динамики процесса ПЭ представляет собой апериодическое звено второго порядка с постоянными времени Т1 и Т2. Его передаточная функция имеет вид:
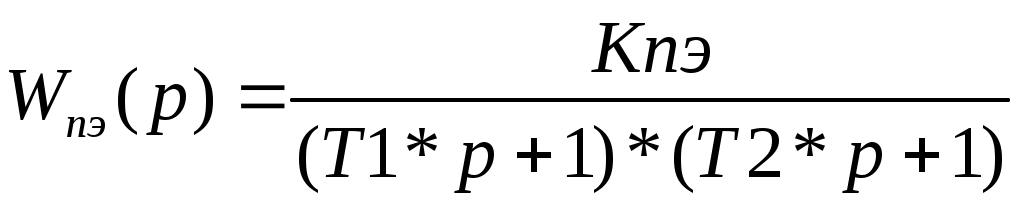 , ,
значения постоянных времени даны в таблицах, коэффициент Кпэ=Uc/10=11В,
Тогда 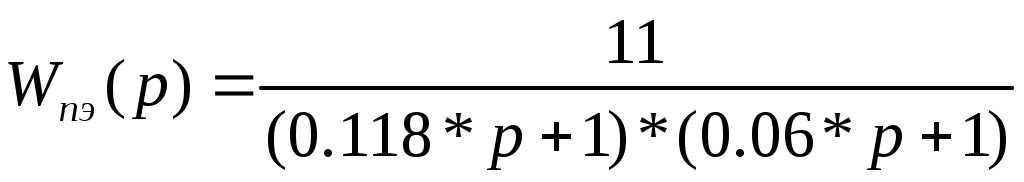 . .
Двигатель. Используя систему уравнений (2) двигателя
U=E+I*R+L*dI/dt;
E=Ce*Ф* ω; (2)
M=Mc+J*d ω/dt;
M=Cm*Ф*I;
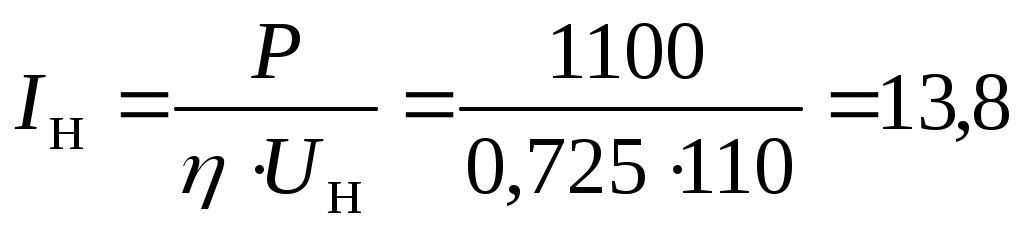 А А
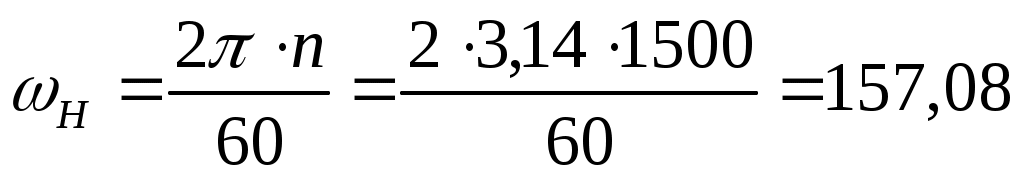 рад/с рад/с
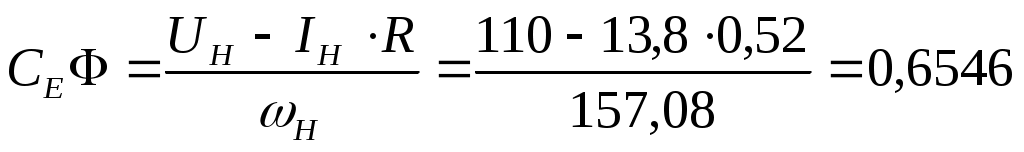 В*с/рад В*с/рад
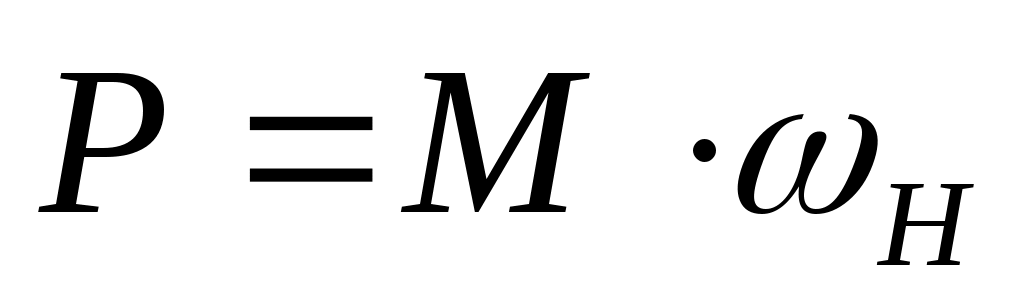  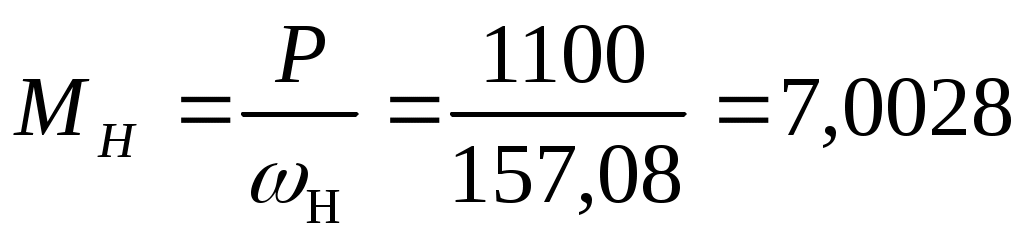 Н*м Н*м
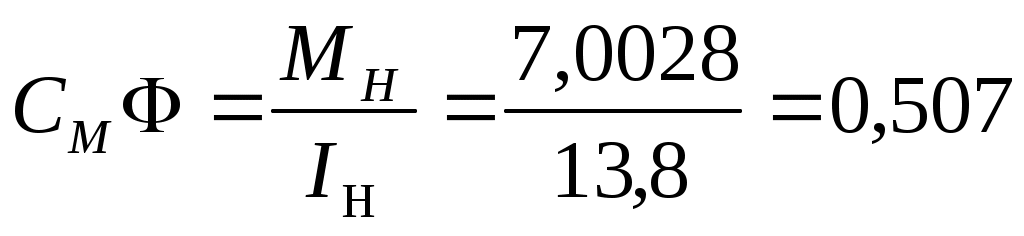 Н*м/А Н*м/А
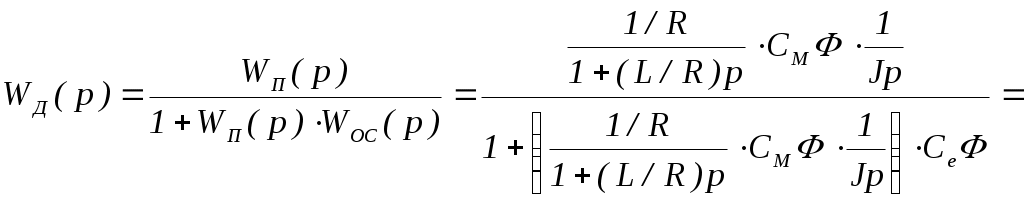
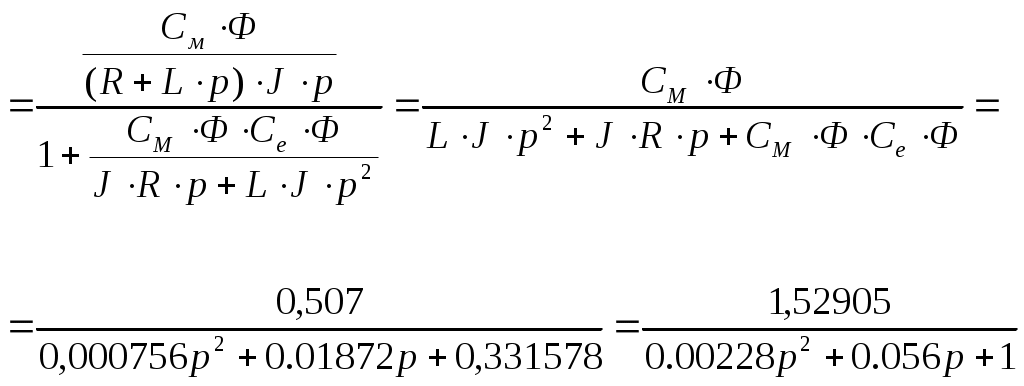
, его структурную схему можно представить следующим образом:
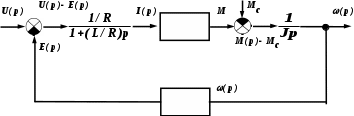
Рисунок 4. Структурная схема электродвигателя
Передаточное устройство является линейным звеном. С точки зрения динамики является апериодическим звеном первого порядка с постоянной времени Тпу, тогда Wпу(р)=Кпу/(Тпу*р+1),
Тпу=0, следовательно
Wпу(р)=Sном/n ном, Wпу(р)=0.21/1500=0.00014
Процесс резания (ПР) описывается уравнением
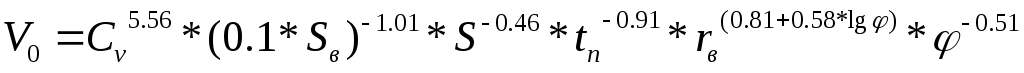
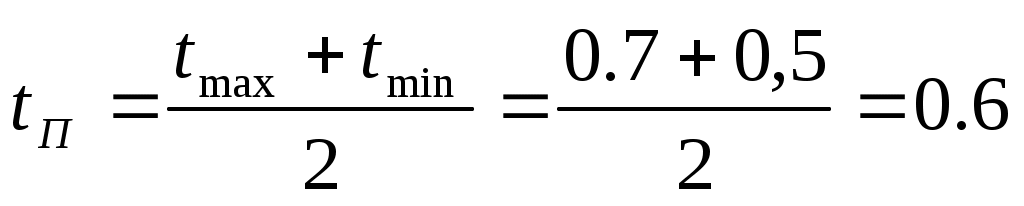 мм мм
Модель нелинейна, необходимо провести линеаризацию функциональных преобразователей (ФП) и умножителей.
1) 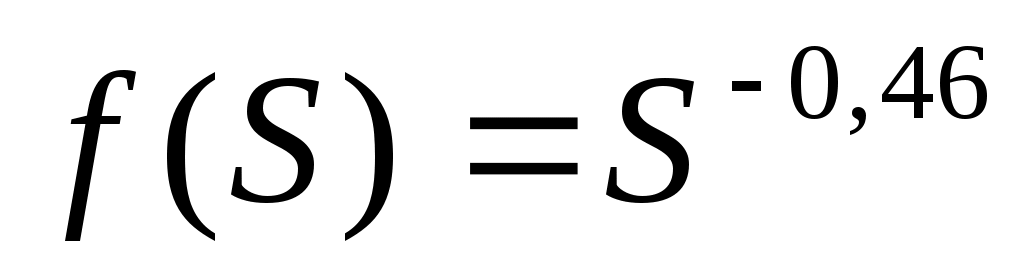
Линеаризуем эту зависимость. Составим уравнение касательной к уравнению 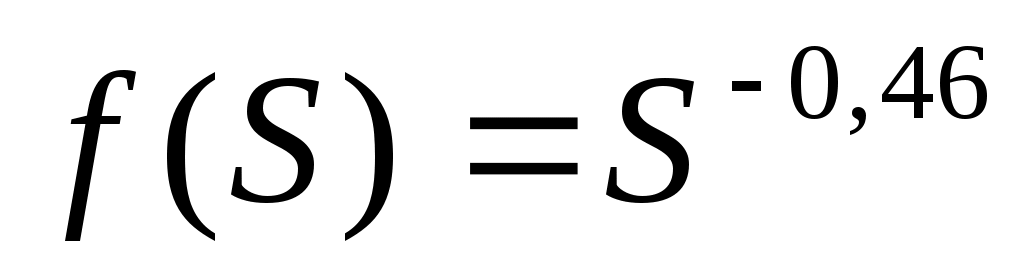 в рабочей точке в рабочей точке 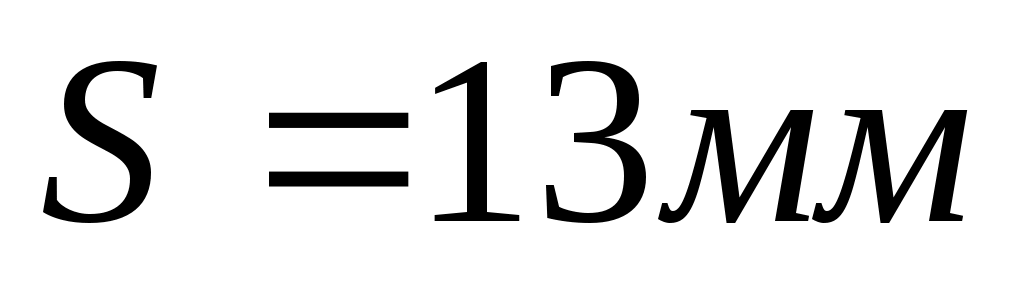 , которое имеет вид: , которое имеет вид:
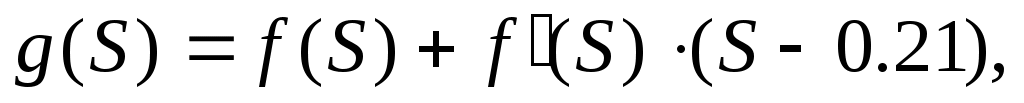
где 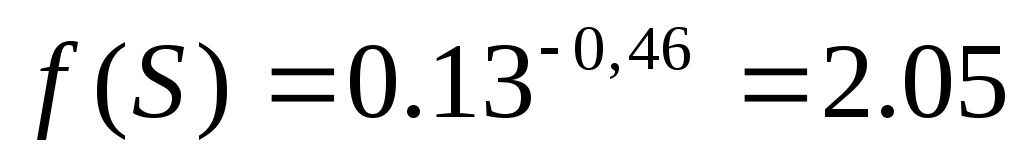
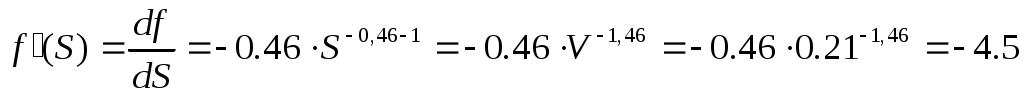
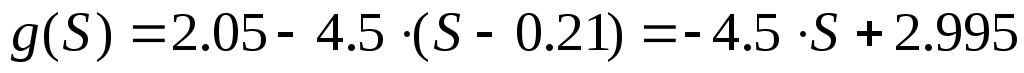
Линеаризовав, получили уравнение касательной 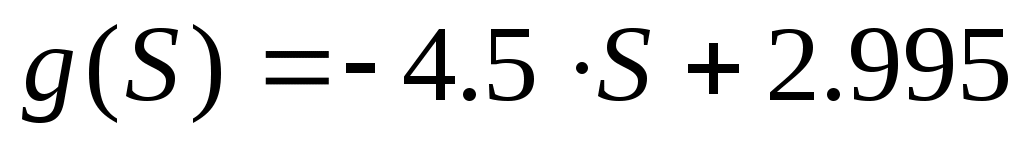 где где 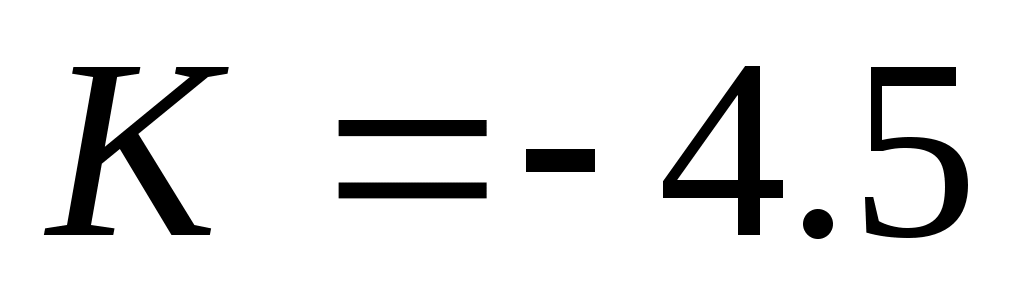 – тангенс угла наклона касательной в рабочей точке – тангенс угла наклона касательной в рабочей точке 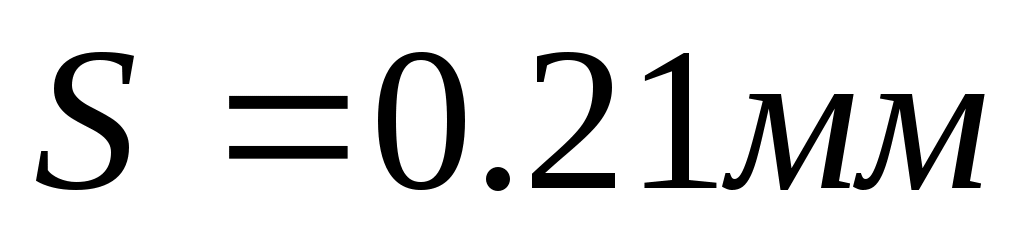 , , 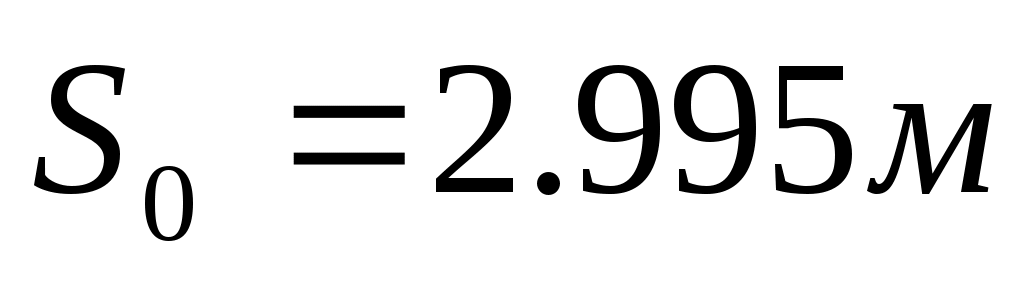 – отклонение касательной от начала координат. – отклонение касательной от начала координат.
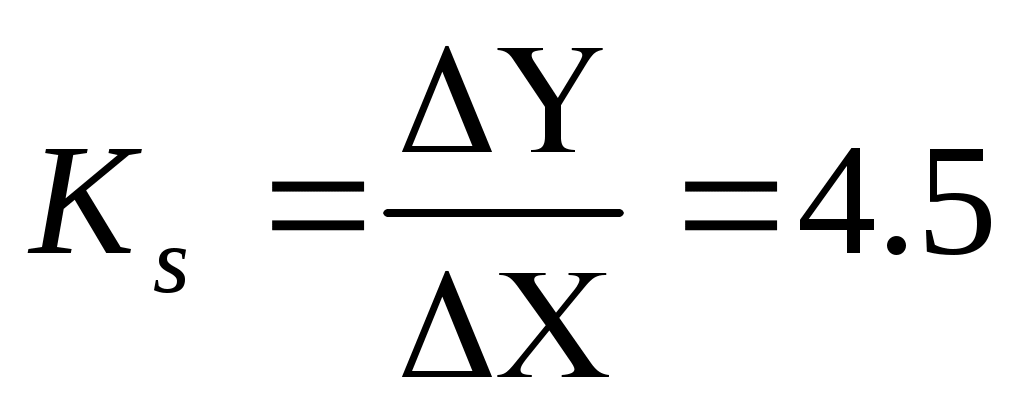
2)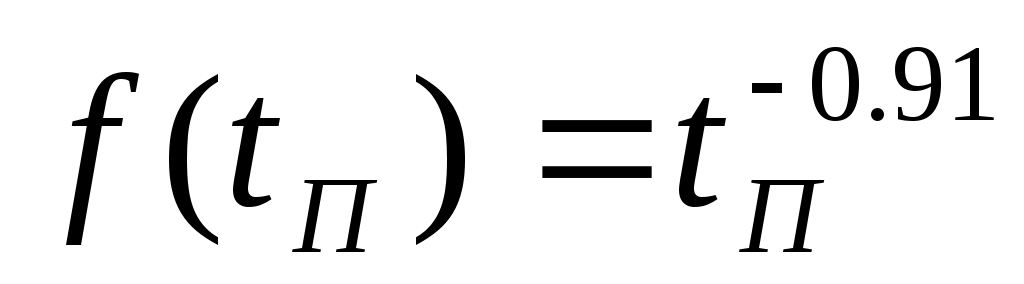
Линеаризуем эту зависимость. Составим уравнение касательной к уравнению в точке 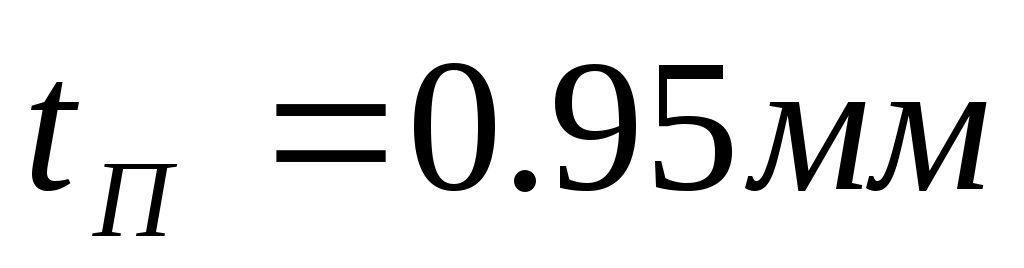 , которое имеет вид: , которое имеет вид:
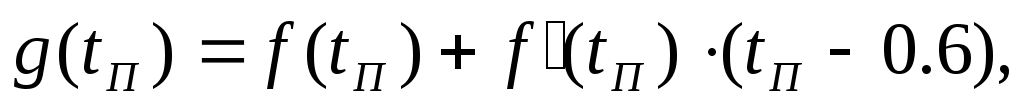
где 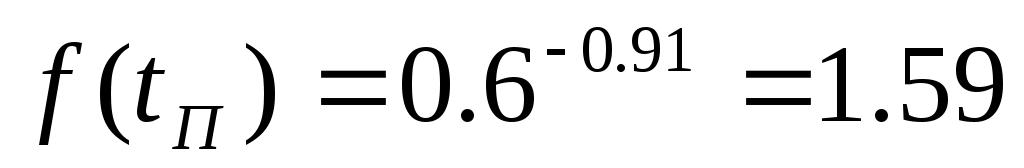
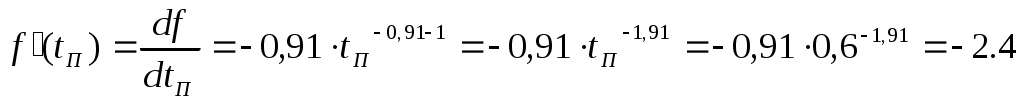
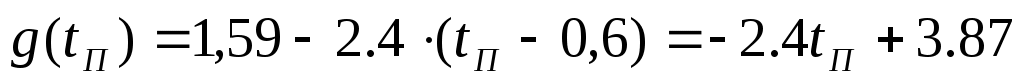
Линеаризовав, получили уравнение касательной, 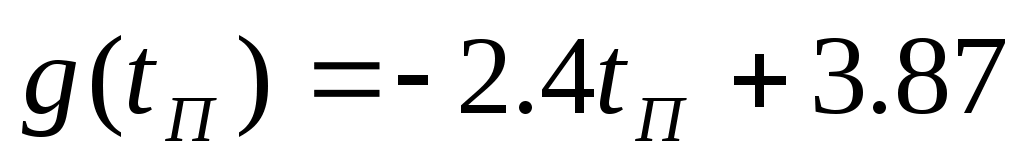 , где , где 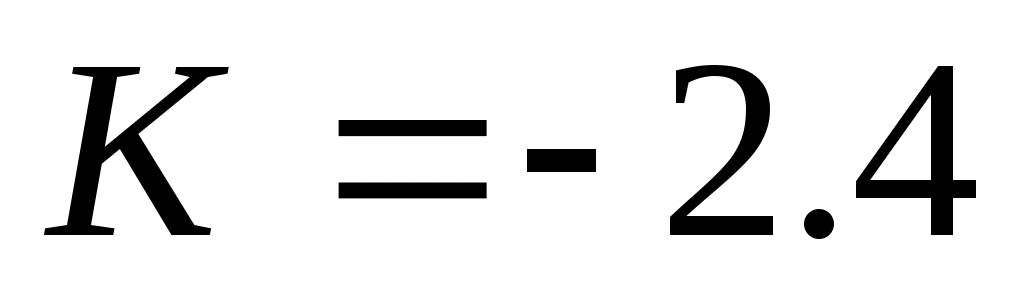 – тангенс угла наклона касательной в рабочей точке – тангенс угла наклона касательной в рабочей точке 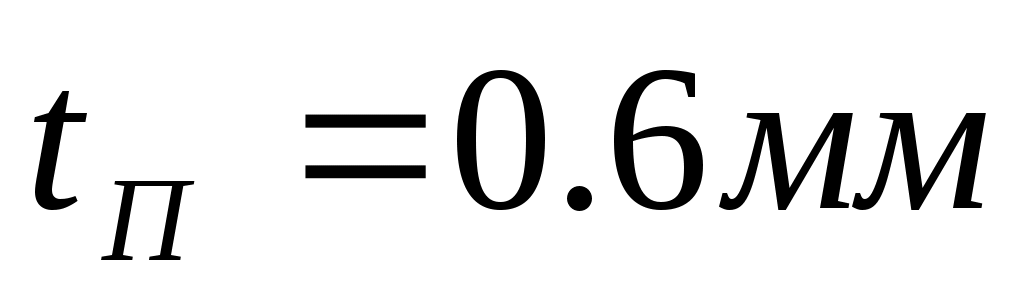 , , 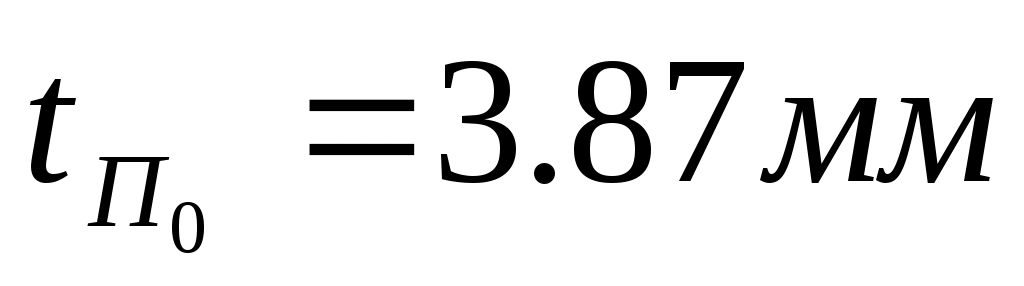 – отклонение касательной от начала координат. – отклонение касательной от начала координат.
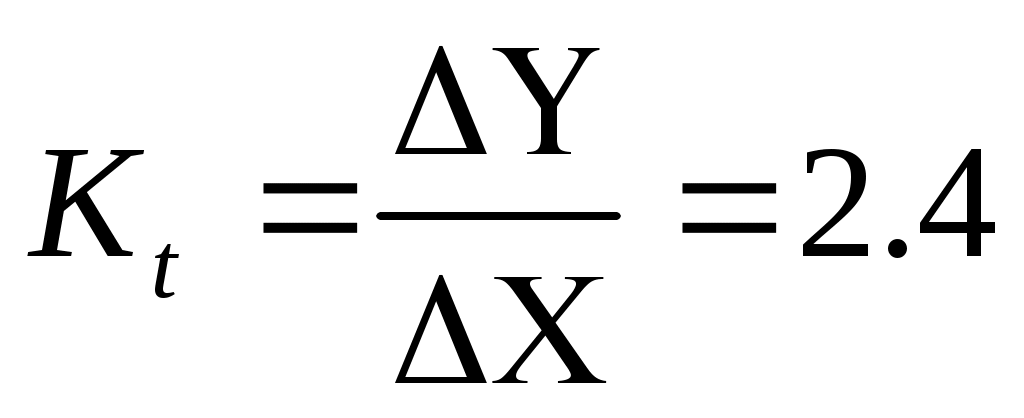
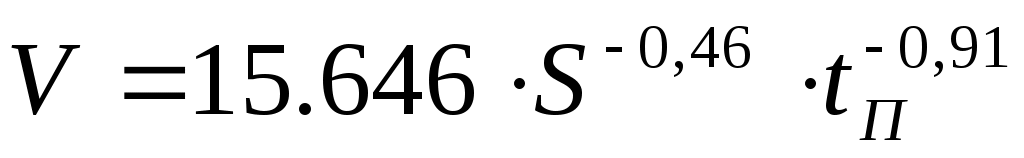 , м/мин , м/мин
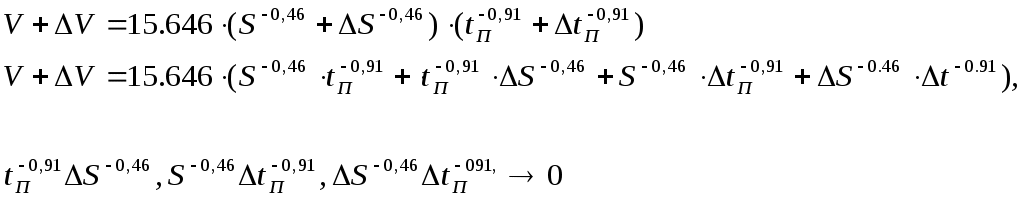
(произведение малых приращений можно не учитывать)
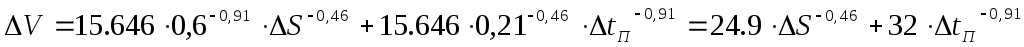
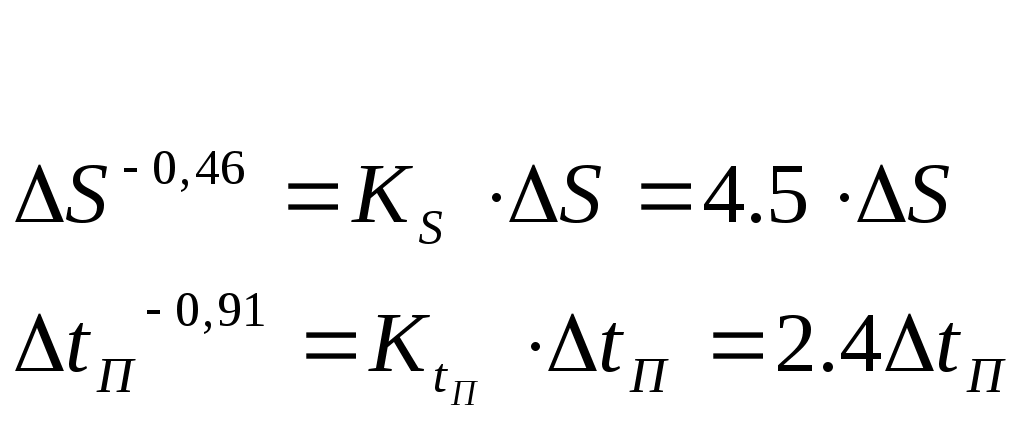
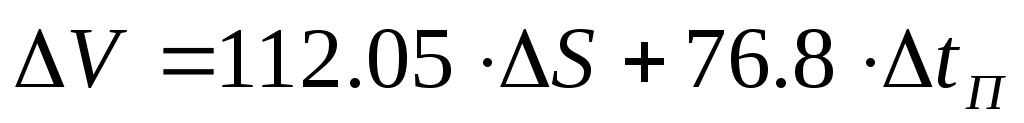
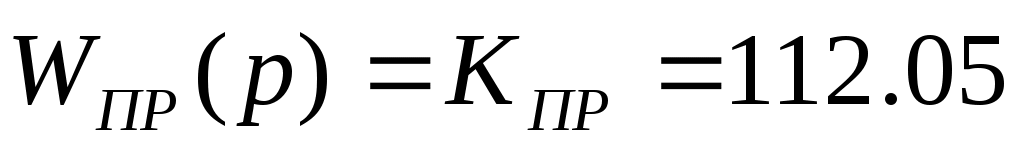
Датчик обратной связи
Wду(р)=Кду/(Тду*р+1), тогда
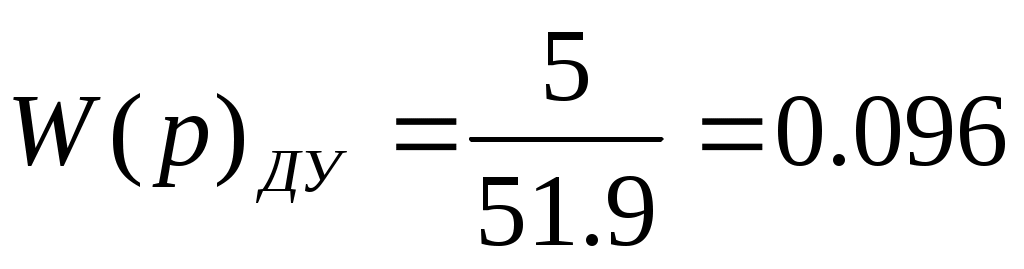
Усилитель УС. Является безинерционным звеном, его передаточную функцию находим из условия:
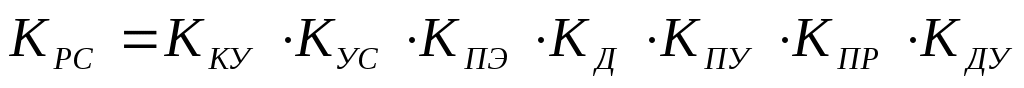 , ,
где 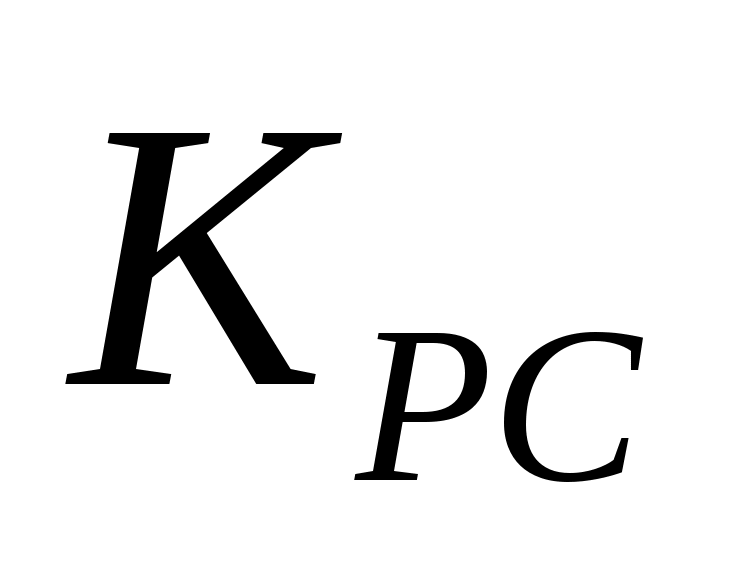 находим из условия: находим из условия: 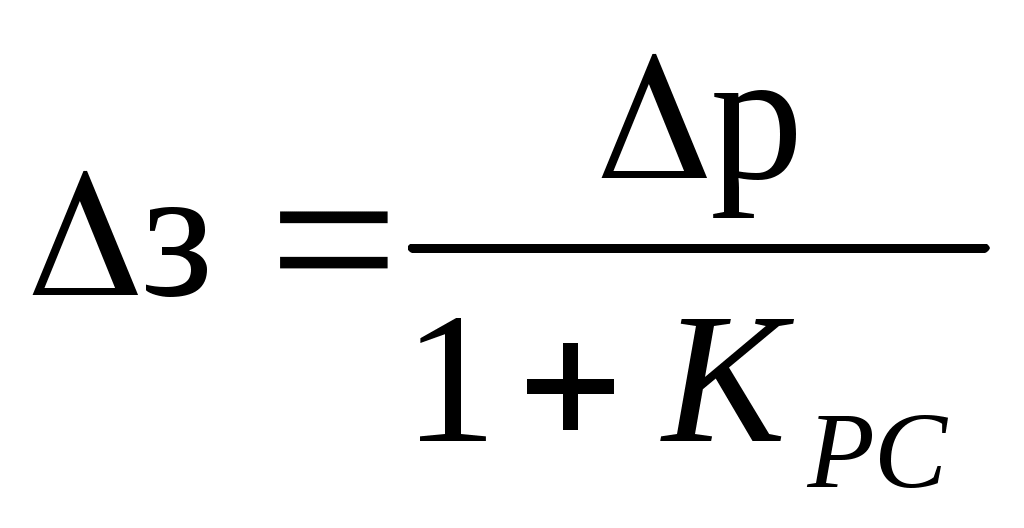
 КРС=216,4; КРС=216,4;

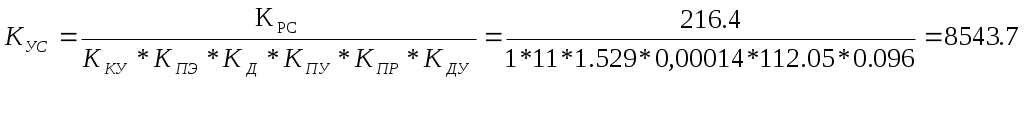
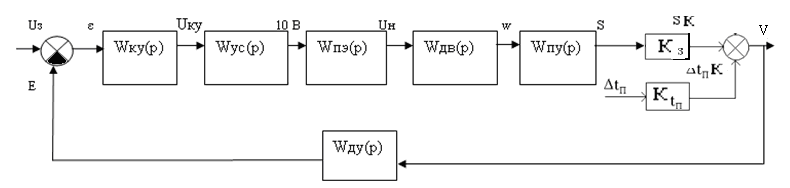
Рисунок 5. Структурная схема скорректированной САР
Корректирующее устройство
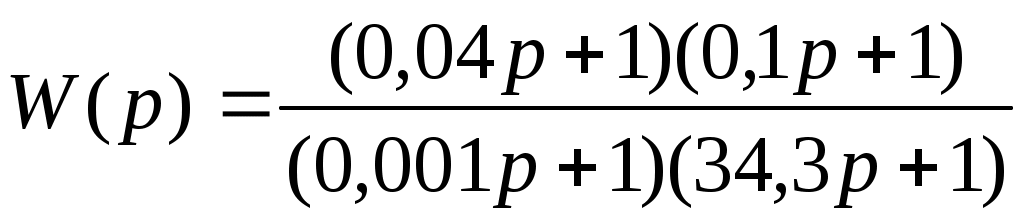
Основной контур системы 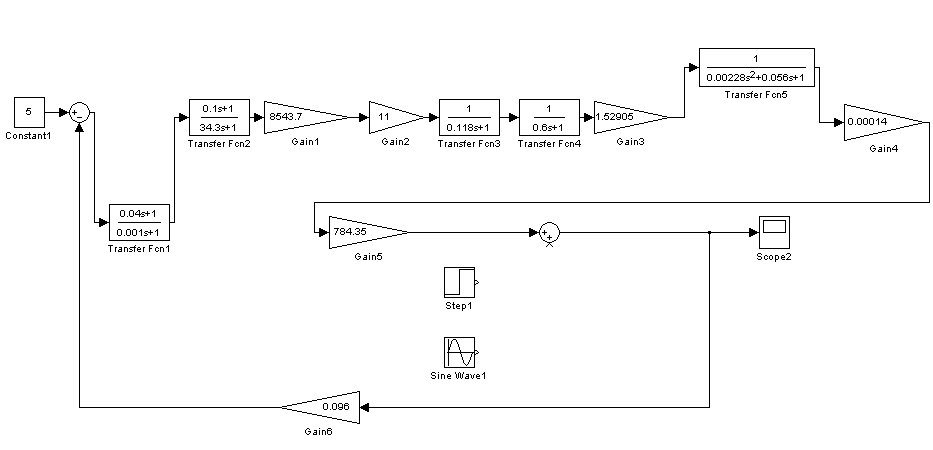 Рисунок 6. Основной контур системы
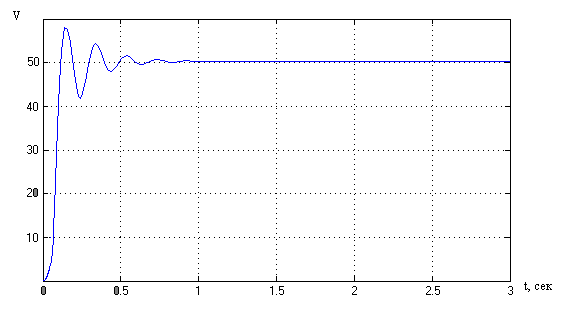
Рисунок 7. Переходный процесс замкнутой Сау без возмущений
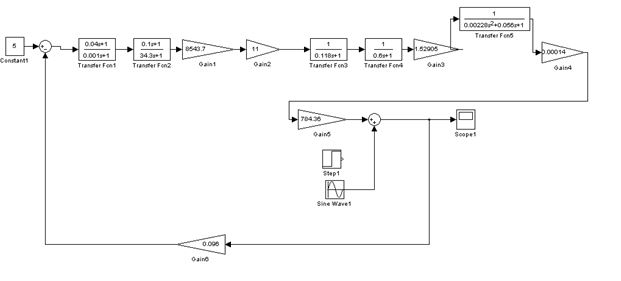
Рисунок 8.основной контур системы с подачей возмущений. 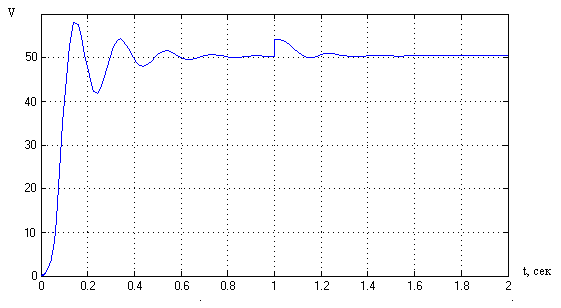 Рисунок 9. Переходный процесс замкнутой САР при максимальном скачке возмущения. Обоснование необходимости применения адаптивного управления
Обычные (неадаптивные) системы управления рассматриваются, исходя из следующих предпосылок:
1) характер возмущающих воздействий на систему управления известен;
2) структура и параметры объекта управления и управляющего устройства остаются неизменными в процессе управления.
Однако в действительности:
1) параметры и структура объекта управления могут меняться непредвиденным образом в процессе функционирования системы управления;
2) характер возмущающих воздействий, принятых при расчете может не соответствовать их действительным характеристикам.
Все эти отличия на практике приводят к расстройке системы, отклонению от расчетных режимов работы, ухудшению показателей качества управления, потере устойчивости. Задача управления усложняется.
Управление такими объектами возможно в том случае, если тем или иным способом организовать получение и использование оперативной информации о происходящих в ОУ изменениях. Это и есть адаптация.
АдСУ состоит из двух частей:
1) Основная система управления, образованная контуром: УУо – ОУ – ОС (устройство управления основным контуром – объект управления – обратная связь).
2) Контур адаптации УУа, осуществляющий настройку основного контура, изменяя его параметры или структуру с целью обеспечения необходимого качества процессов управления при изменяющихся условиях работы. Контур адаптации – второй уровень управления.
Коэффициент передачи процесса резания может изменяться в большое количество раз. На изменение 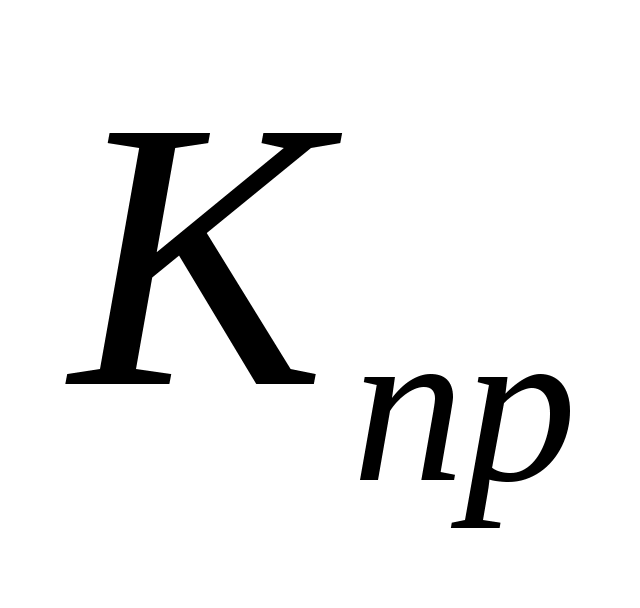 могут оказывать влияние следующие факторы: величина припуска tп, изменение условий среды, в которой происходит обработка, изменение физико-химических свойств обрабатываемого и инструментального материала. При таких вариациях коэффициента передачи процесса резания обычные САР скоростью резания с постоянными параметрами корректирующих и управляющих элементов не смогут обеспечить требуемые условия точности в изменяющихся условиях процесса резания. Например, при могут оказывать влияние следующие факторы: величина припуска tп, изменение условий среды, в которой происходит обработка, изменение физико-химических свойств обрабатываемого и инструментального материала. При таких вариациях коэффициента передачи процесса резания обычные САР скоростью резания с постоянными параметрами корректирующих и управляющих элементов не смогут обеспечить требуемые условия точности в изменяющихся условиях процесса резания. Например, при
На практике часто случается так, что 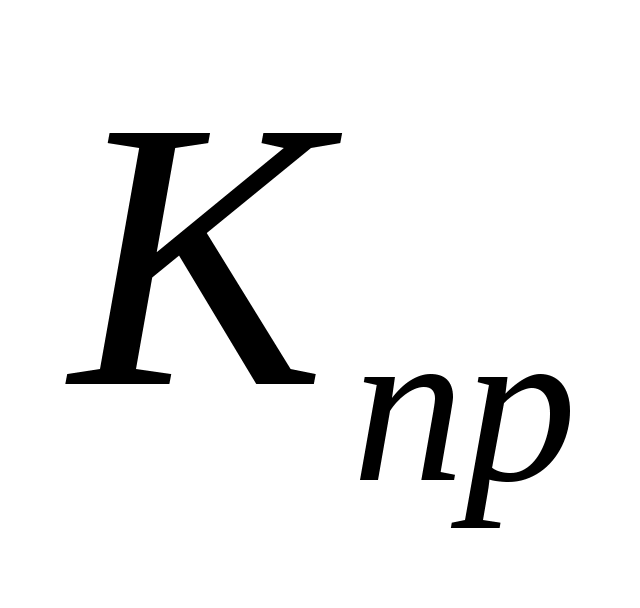 изменяется в несколько раз из-за изменений среды, в которой находится объект управления. В этом случае может произойти потеря устойчивости, что крайне не желательно на производстве. изменяется в несколько раз из-за изменений среды, в которой находится объект управления. В этом случае может произойти потеря устойчивости, что крайне не желательно на производстве.
Пусть 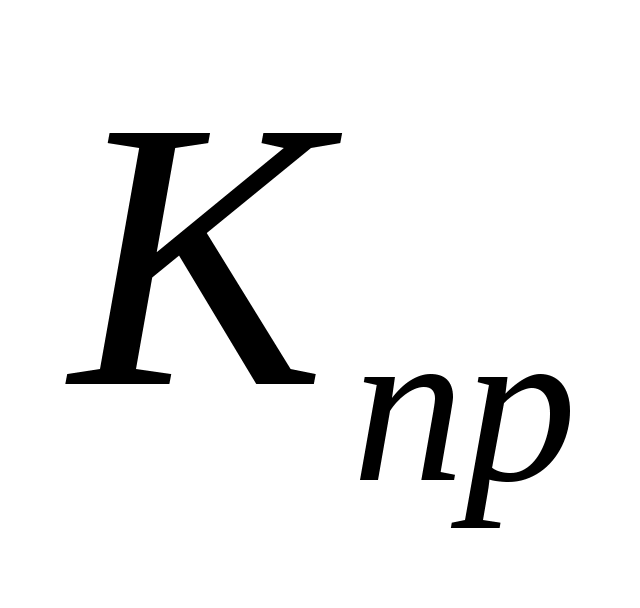 увеличился в 2 раз. Тогда в системе будут наблюдаться неустойчивые колебания: увеличился в 2 раз. Тогда в системе будут наблюдаться неустойчивые колебания:
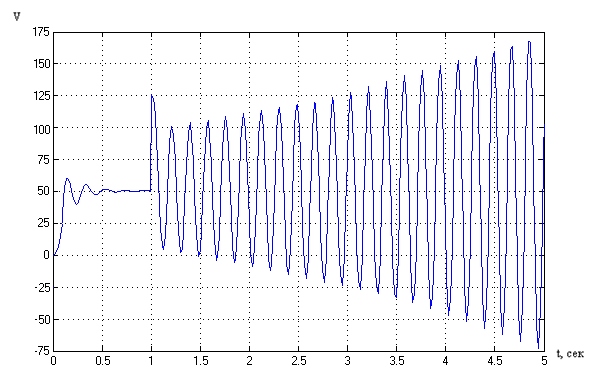
Рисунок10. Переходной процесс при изменении Кпр в 3 раза.
Из рисунка видно, что система будет выходить из строя при большом изменении 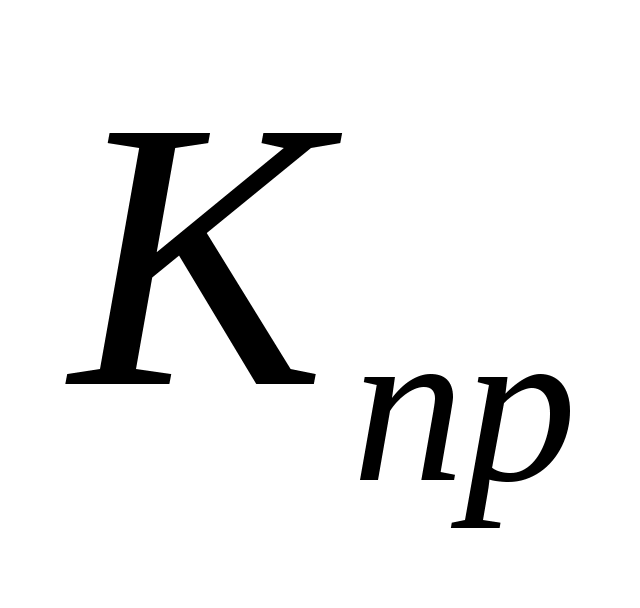 . .
При пульсирующем изменении Кпр .
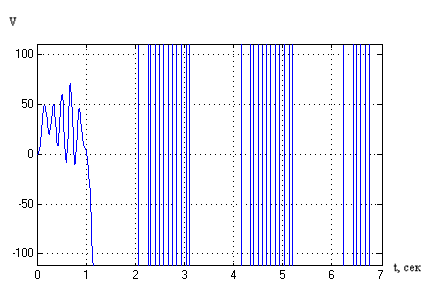
Рисунок11. работа классической системы при пульсирующем изменении Кпр.
Из рис.10, рис.11 видно, что классическая система плохо приспособлена для практического применения, так как на нее влияет пульсация и значительное увеличение Кпр. Для обеспечения требуемых свойств системы необходимо синтезировать структуру АдСУ, инвариантную к изменению коэффициента передачи объекта управления.
Выбор класса адаптивной системы управления, функциональная схема
В тех случаях, когда изменения параметров объекта настолько значительны, что классические принципы управления становятся недостаточными, а контуры систем управления с неизменной настройкой – практически непригодными, возникает мысль о введении в систему дополнительных управляющих органов, осуществляющих перестройку параметров контура управления (как правило, управляющего устройства, поскольку изменять параметры объекта обычно технически трудно). Наиболее распространенной и простой в реализации адаптивной системой является самонастраивающаяся система с замкнутым контуром адаптации. Так как задача адаптации – поддержание заданной величины, то в нашем случае будет применена система со стабилизацией качества. Функциональная схема такой системы приведена на рис.12
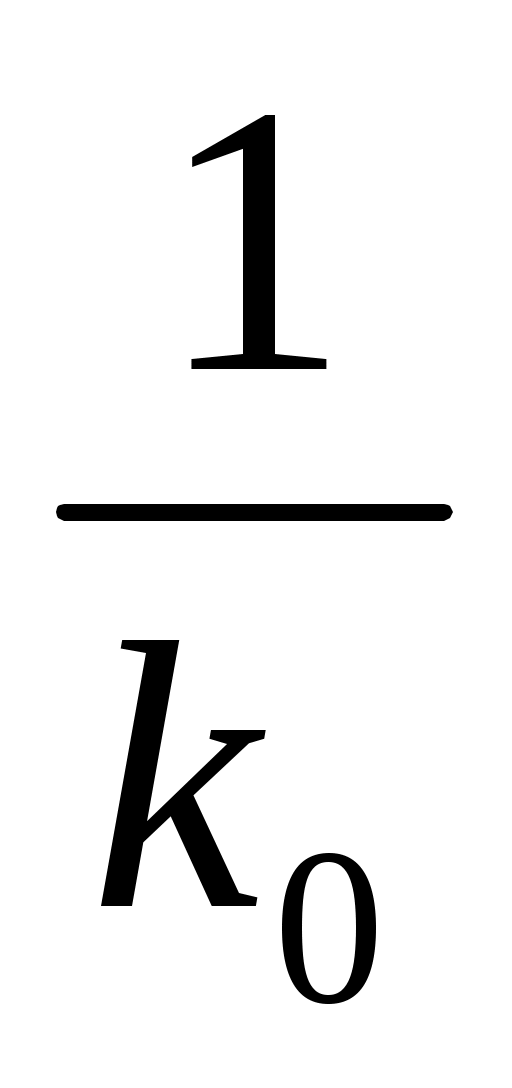
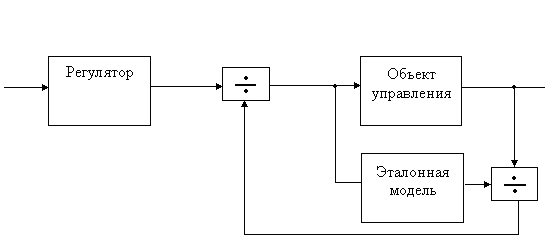 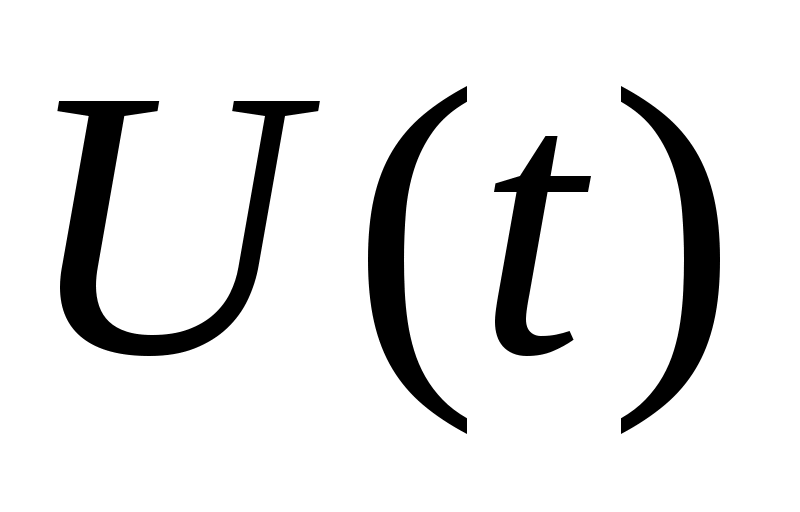 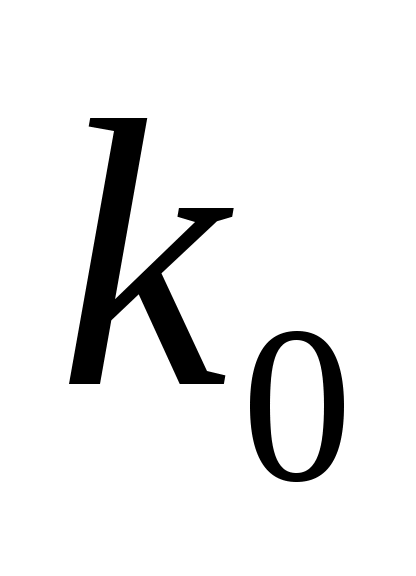 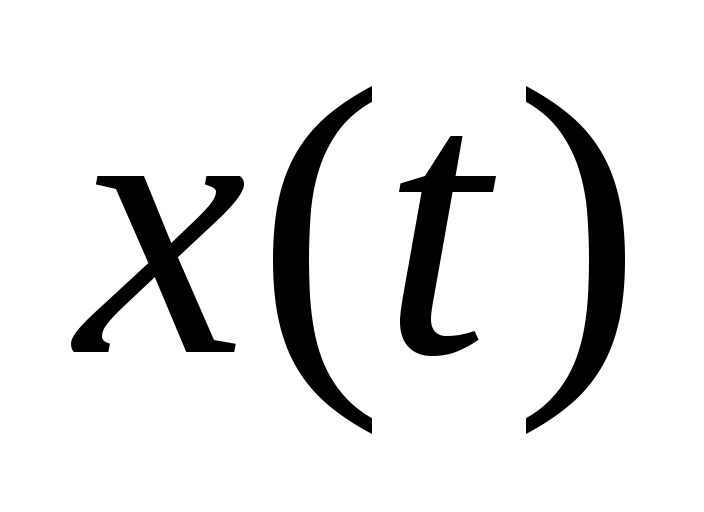 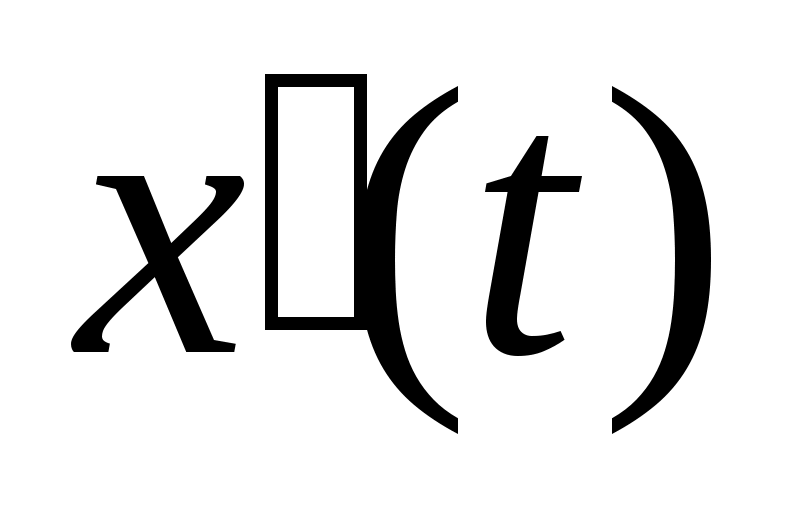 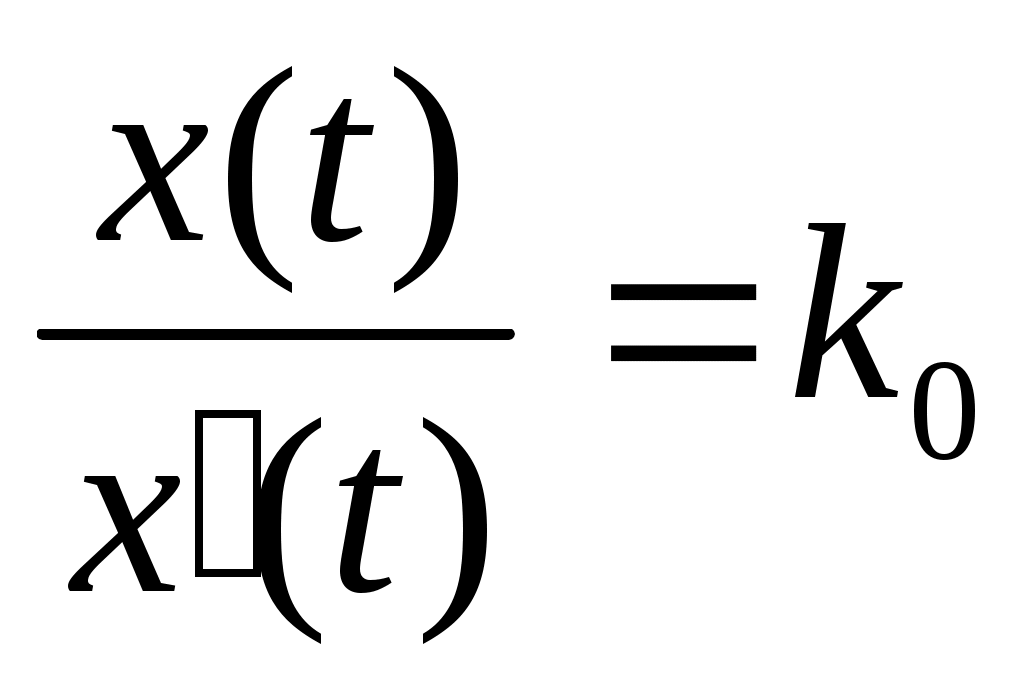
Рисунок 12. Схема СНС с эталонной моделью.
В качестве объекта управления будем понимать процесс резания, двигатель и передаточное устройство. Сигнал U(t) одновременно поступает на объект управления и на его эталонную модель. Снятый с объекта управления сигнал X(t) делится на сигнал с эталонной модели X’(t). Далее полученный коэффициент K0 возводится в степень -1 и вводится в основной контур. Тем самым обеспечивается неизменность коэффициента разомкнутой системы, она становится стационарной.
Разработка структурной схемы адаптивной системы управления, расчет элементов контура адаптации
Определим параметры адаптивного контура для исходной системы. Динамика эталонной модели определяется динамикой электродвигателя и передаточного устройства:
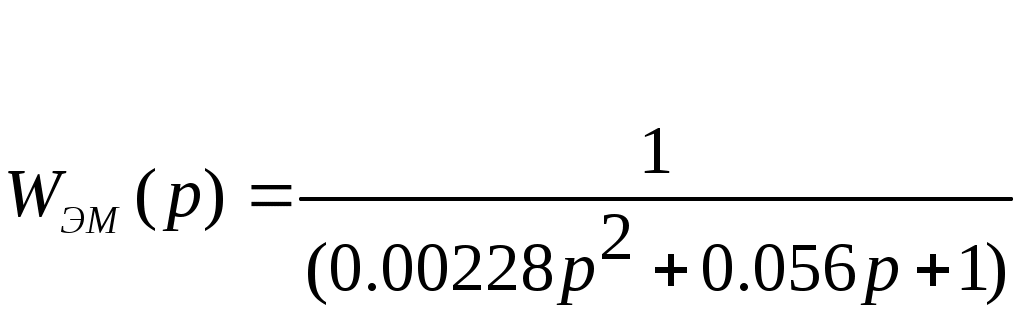
После выхода из первого блока деления мы получаем величину Ко реального объекта управления, который является делителем второго блока деления. После прохождения второго блока деления сигнал становится равным 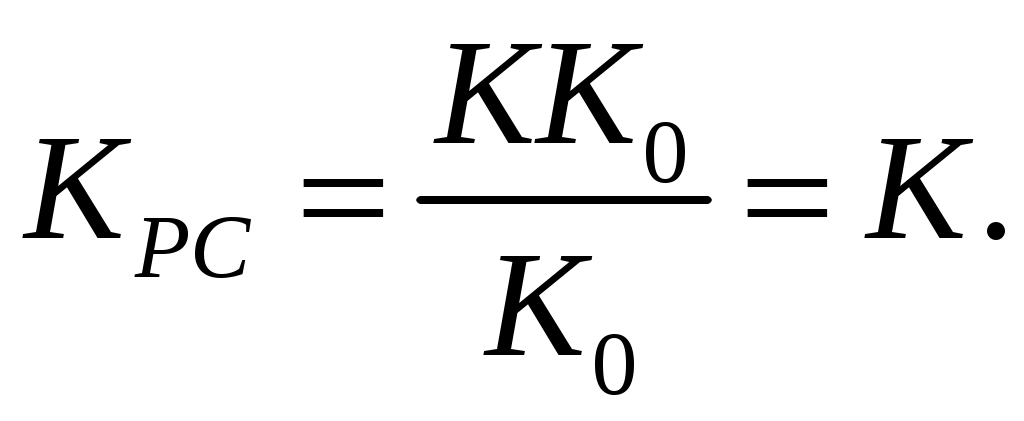 Где: Где: 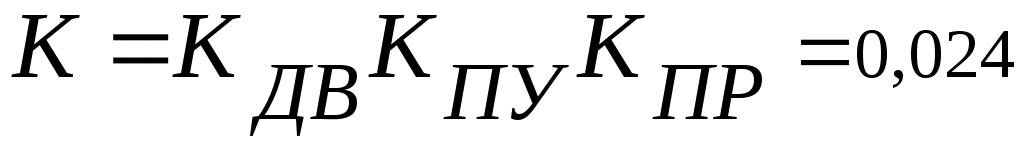 . Этот коэффициент необходимо добавить в регулятор, для того, что бы коэффициент передачи системы в целом не изменился и оставался равным К, относительно которого была спроектирована система. . Этот коэффициент необходимо добавить в регулятор, для того, что бы коэффициент передачи системы в целом не изменился и оставался равным К, относительно которого была спроектирована система.
В схеме используется два блока деления. При этом в начальный момент времени все сигналы равны 0. Это может вызвать некорректность работы, так как деление на 0 недопустимо. Для того, чтобы устранить этот эффект подадим на вход блока деления небольшой сигнал. Полученная система приведена на рис.13
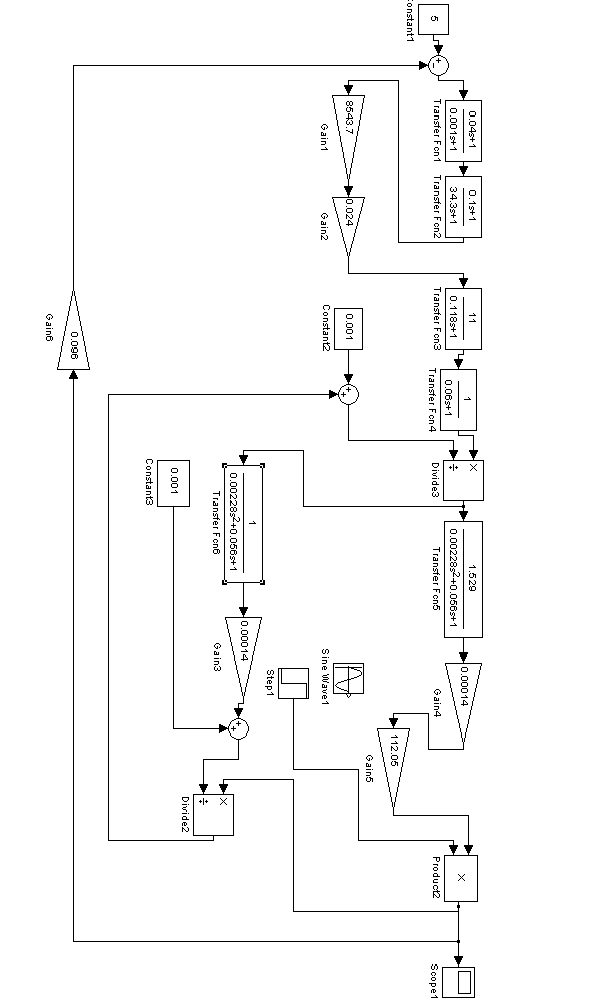
Рисунок 13. Структурная схема АдСУ.
Выводы о качестве работы АдСУ по результатам моделирования
В результате моделирования разработанной АдСУ были получены следующие результаты: 1) Переходный процесс Сау с адаптивным контуром без возущений. 
Рисунок 14. Переходный процесс
2) При скачкообразном увеличении Кпр в 2 раз система не выходит из строя, что наблюдалось для классической системы, а продолжает работать.
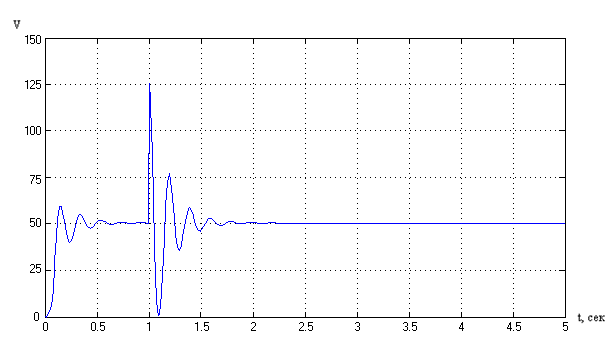
Рисунок 15 Переходный процесс при увеличении Кпр в 2 раза с контуром адаптации.
3) При скачкообразном увеличении Кпр в10 раз система не выходит из строя, а продолжает работать.
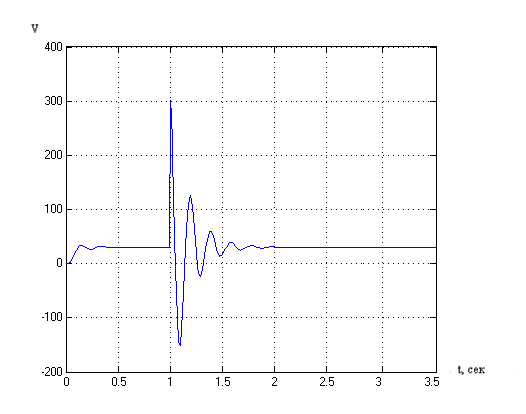
Рисунок 16. Переходный процесс при увеличении Кпр в 10раза с контуром адаптации.
4) При пульсирующем изменении Кпр (увеличение в 1-3 раза) с частотой 0,2 Гц (период колебаний 5с.) АдСУ стабильно работает, подстраиваясь к изменению параметров объекта управления

Рисунок 17. Переходный процесс при действии на процесс резания пульсирующего возмущения
(Кпр изменяется в 1-3 раза с частотой 0,2 Гц).
5) При значительном увеличении частоты пульсации Кпр (до 1 Гц, период 1с.) система “не успевает” подстраиваться к изменению объекта управления
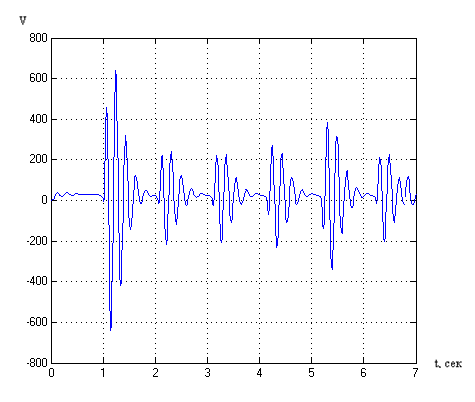
Рисунок 18. Переходный процесс при действии на процесс резания пульсирующего возмущения.
Заключение В процессе выполнения работы из классической системы управления скоростью резания была спроектирована адаптивная система. Она отличается тем, в ней обеспечена стационарность, то есть она не зависит от изменения Кпр. Даже при очень большом увеличении Кпр (в 10 раз) система продолжает стабильно работать. Разработанная АдСУ более приспособлена к практическому применению, нежели классическая. Только при очень быстром изменении пульсирующего внешнего воздействия спроектированная система “не успевает” подстроиться.
Список литературы
1. Бесекерский В.А. «Сборник задач по теории автоматического регулирования и управления» - М.: Наука, 1978г.
2. Топчеев Ю.И. «Атлас для проектирования систем автоматического регулирования» - М.: Машиностроение, 1989г.
3. Копылов И. П. Справочник по электрическим машинам, том 1. Москва Энергоатомиздат, 1988.
4. А.А.Воронов «Основы теории автоматического регулирования и управления, М., Высшая школа, 1997.
|
|
|
 Скачать 0.54 Mb.
Скачать 0.54 Mb.


 ∆tп
∆tп 

 S Процесс резания V
S Процесс резания V 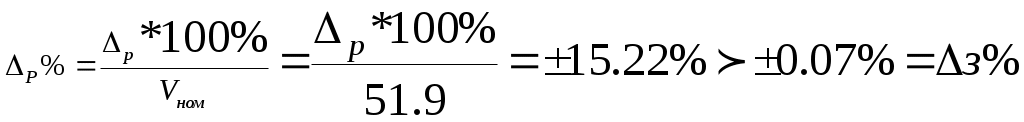
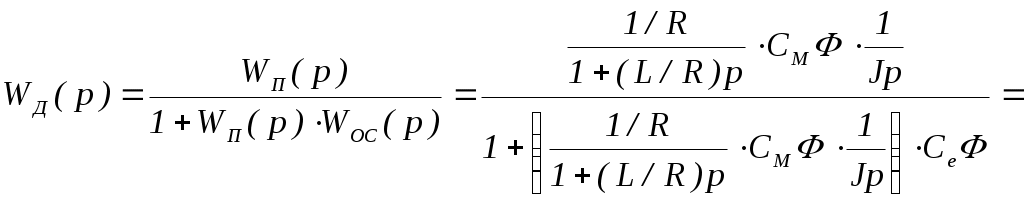
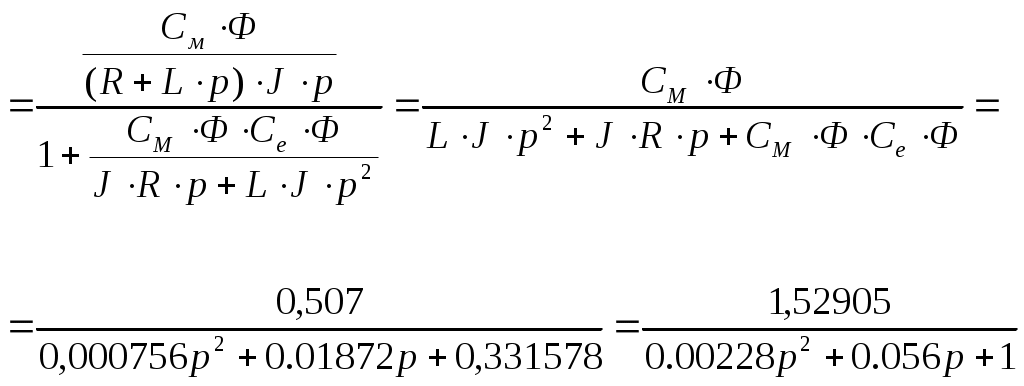

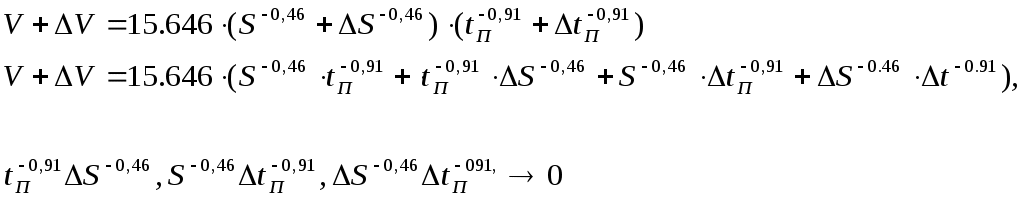
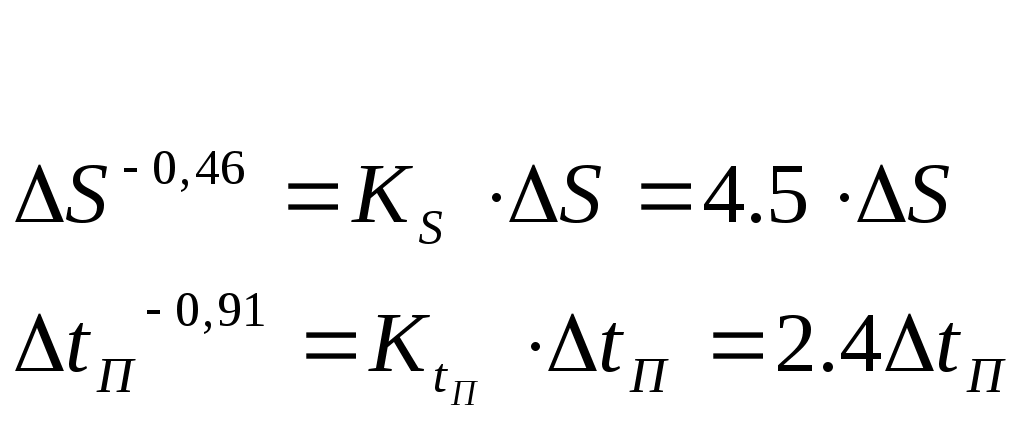
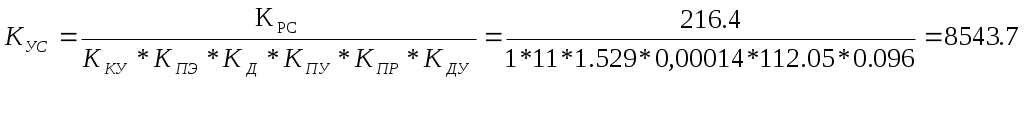









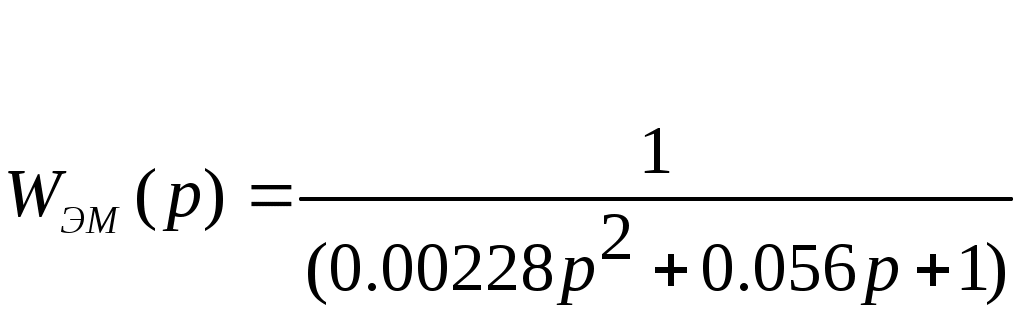
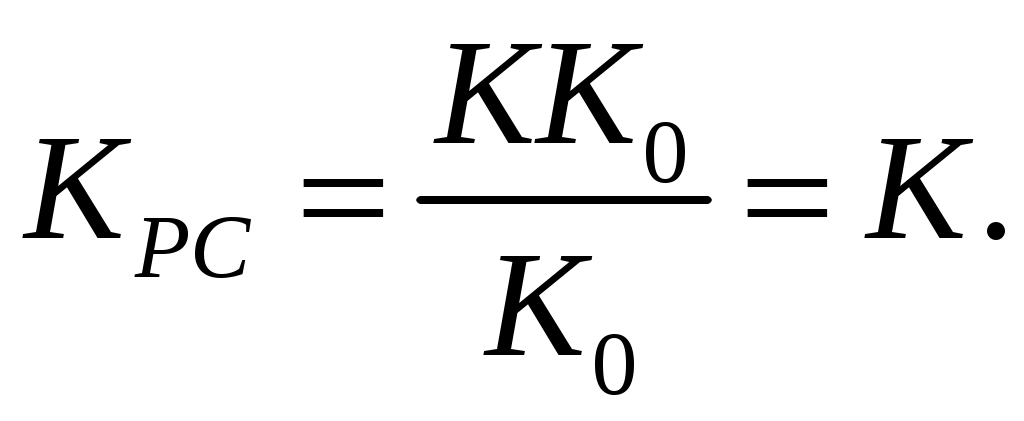 Где:
Где: 


