Синтез адаптичной системы управления. Синтез адаптивной системы управления. Синтез адаптивной системы управления в пакете MatLab
 Скачать 290.58 Kb. Скачать 290.58 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФГБОУ ВО «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» ФАКУЛЬТЕТ ЭНЕРГЕТИКИ И СИСТЕМ УПРАВЛЕНИЯ КАФЕДРА «ЭЛЕКТРОПРИВОДА АВТОМАТИКИ И УПРАВЛЕНИЯ В ТЕХНИЧЕСКИХ СИСТЕМАХ» Курсовая работа по дисциплине: «Управление в условиях неопределенности» на тему: «Синтез адаптивной системы управления в пакете MatLab» Выполнил: студент гр. мТСУ - 201 Дудченко Д.А. Проверил: Воронеж 2021 Содержание Введение………………………………………………………………………..….3 Анализ исходных данных………………………………………………..4 Анализ технологического процесса как объекта управления………...6 Структура основного контура системы………………………………...8 Математическая модель ОУ…………………………………………….9 Обоснование применения адаптивного контура……………………..10 Разработка структурной схемы АдСУ………………………………...11 Моделирование АдСУ на ЭВМ………………………………………..12 Заключение………………………………………………………………………20 Список использованной литературы…………………………………………...21 Введение В последние десятилетия возникла необходимость осуществлять автоматическое управление объектами, параметры которых в результате изменений во внешней среде также изменяются в широком диапазоне. К такого рода объектам прежде всего относятся промышленные объекты, работающие на сырье с сильными случайными колебаниями параметров, летающие объекты – самолеты и ракеты, проникающие в верхние слои атмосферы. Параметры и структура систем управления могут меняться непредвиденным образом в процессе функционирования системы управления, характер возмущающих воздействий, принятых при расчете может не соответствовать их действительным характеристикам. Все это на практике приводит к расстройке системы, отклонению от расчетных режимов работы, снижению качества управления и даже к потере устойчивости. В последнее время установилось более или менее общепризнанное представление об одном из наиболее разработанных и распространенных в практике классе адаптивных систем, получивших название самонастраивающихся (СНС), разработка одной из которых является основной целью данной курсовой работы. Анализ исходных данных Схема взаимодействия электропривода и процесса резания приведена на рис. 1: . 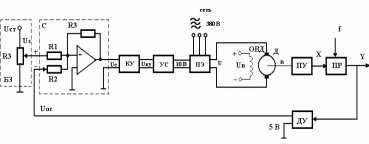 Рис.1. Функциональная схема САР выходной координаты САР регулирует выходную координату процесса резания с заданной точностью. Процесс резания на схеме обозначен функциональным блоком ПР. ПУ – передаточное устройство, это механическая система, преобразующая механическую энергию вала двигателя в механическую энергию управляющего воздействия процесса резания. ПУ является линейным звеном. С точки зрения динамики является апериодическим звеном первого порядка с постоянной времени 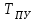 . Двигатель Д преобразует электрическую энергию в механическую энергию вращения вала. Двигатель является машиной постоянного тока с независимым возбуждением. Возбуждение машины осуществляется обмоткой ОВД. Поток возбуждения в процессе регулирования не изменяется и остается равным его номинальному значению. Регулирование скорости двигателя осуществляется изменением напряжения якоря U. . Двигатель Д преобразует электрическую энергию в механическую энергию вращения вала. Двигатель является машиной постоянного тока с независимым возбуждением. Возбуждение машины осуществляется обмоткой ОВД. Поток возбуждения в процессе регулирования не изменяется и остается равным его номинальному значению. Регулирование скорости двигателя осуществляется изменением напряжения якоря U.ПЭ – преобразователь электрической энергии, преобразует электрическую энергию промышленной сети трехфазного переменного тока в электрическую энергию постоянного тока и регулирует величину выходного напряжения U, питающего цепь якоря двигателя Д. Преобразователь электрической энергии является линейным звеном. Выходное напряжение U равно номинальному значению при напряжении управления 10 В. С точки зрения динамики процесса ПЭ представляет собой апериодическое звено второго порядка с постоянными времени 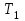 и и 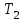 . .УС – усилитель, является безынерционным звеном, усиливает напряжение, поступающее от корректирующего устройства. КУ – корректирующее устройство, корректирует динамические свойства САР. Статический коэффициент передачи КУ равен 1. БЗ – блок задания. Блоком задания задается напряжение 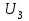 , его величина определяет величину задания выходной координаты САР. БЗ содержит в себе источник стабилизированного напряжения , его величина определяет величину задания выходной координаты САР. БЗ содержит в себе источник стабилизированного напряжения 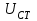 и резистор R3. и резистор R3. 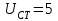 В. В.ДУ – измерительная система выходной координаты процесса резания. С точки зрения динамики представляет собой апериодическое звено первого порядка с постоянной времени 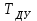 . При номинальном значении выходной координаты выдаёт напряжение . При номинальном значении выходной координаты выдаёт напряжение 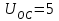 В. В.С – сумматор на базе операционного усилителя и на резисторах R1, R2, R3. Является безынерционным звеном с коэффициентом передачи равным 1. Суммирование осуществляется по алгоритму 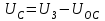 . . Функциональная схема САР представлена на рис.2: 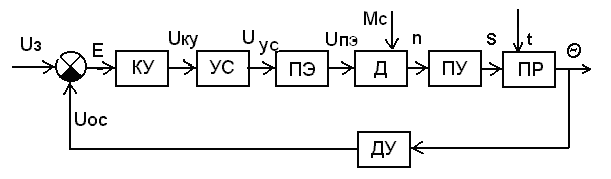 Рис. 2 Функциональная схема САР По алгоритму функционирования данная САР является следящей. В ней выходная величина – температура в области резания – регулируется с заданной точностью при изменении напряжения на входе, т.е. система управляет выходной координатой. На вход системы подается напряжение 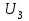 , соответствующее заданной температуре в области резания. Это напряжение сравнивается с напряжением , соответствующее заданной температуре в области резания. Это напряжение сравнивается с напряжением 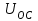 , поступающим с датчика обратной связи – например, естественной термопары. Если существует ненулевая разница этих напряжений – ошибка регулирования , поступающим с датчика обратной связи – например, естественной термопары. Если существует ненулевая разница этих напряжений – ошибка регулирования 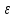 , то она с соответствующим знаком поступает на КУ, таким образом меняет напряжение на своем выходе, чтобы свести ошибку регулирования путем изменения скорости вращения двигателя к минимуму или нулю. Если на систему действуют возмущения, то система с обратной связью будет компенсировать эти возмущения, поддерживая температуру в области резания постоянной. , то она с соответствующим знаком поступает на КУ, таким образом меняет напряжение на своем выходе, чтобы свести ошибку регулирования путем изменения скорости вращения двигателя к минимуму или нулю. Если на систему действуют возмущения, то система с обратной связью будет компенсировать эти возмущения, поддерживая температуру в области резания постоянной.Анализ технологического процесса как объекта управления Анализ процесса резания как объекта управления осуществляется в несколько этапов. 1. Определение состава возможных выходных координат ОУ. В качестве выходной координаты можно выбрать различные параметры процесса резания: температуру в зоне резания, параметры стружки, силу резания, износ инструмента, уровень шероховатости обработанной поверхности и т.д. 2. Выбор выходной координаты, количественно характеризующий ход процесса резания. Выбираем в качестве выходной координаты, количественно характеризующий ход процесса резания - температуру в зоне резания. Исходя из задания и из того, что тепло, возникающее при резании, влияет на большинство факторов – износ и стойкость инструмента, точность обработки, характеристики качества поверхностного слоя и т.д. 3. Математическое описание ОУ. Уравнение  , , 4. Определение состава управляющих координат. В качестве управляющих координат на ОУ оказывают влияние скорость резания 5.Определение состава возмущений. Изменение величины припуска Учитывая вышесказанное, ПР в качестве объекта управления можно представить следующим образом:  Рис. 3. Структурная схема ОУ 6. Определение диапазона изменения возмущений. tп изменяется в пределах от 0,5 до 0,7 мм., т.е. Δtп=0,2 мм. S изменяется от +10% до –15% S3, от 0,1785 до 0,231 т.е. ΔS=0,0525 7. Определение отклонения выходной координаты при совместном действии возмущений. Температура в зоне резания изменяется в следующих пределах: Θмин=267*200,384*0,17850,132*0,50,098=629,62 Θмакс=267*200,384*0,2310,132*0,70,098=673,26 ΔΘ=43,64 8. Определение заданной точности регулирования выходной координаты. По заданию допуск на температуру ±5° С. Структура основного контура системы Структура основного контура системы определяется данными из курсового проекта теории управления:  Рис.4. Структурная система САР  Рис.5 Основной контур системы Переходная характеристика имеет вид (рис.6):  Рис.6. Переходная характеристика замкнутой САР Математическая модель ОУ Параметры возьмем из курсового проекта теории управления: WПЭ(р)=  WПУ(р)=0,0267 WДУ(р)=0,00694 WД(р)=  WКУ(р)=  КУС=357,15 КПР=12,5 Обоснование применения адаптивного контура Обычные (неадаптивные) системы управления (СУ) рассматриваются, исходя из следующих предпосылок: - характер возмущающих воздействий на СУ известен; - свойства (структура и параметры) объекта управления (ОУ) и СУ неизменны. Однако в действительности: - характеристики внешних и внутренних воздействий на СУ могут существенно отличаться от принятых при расчете; - свойства ОУ могут изменяться непредвиденным образом под действием внешних и внутренних факторов. Все эти отличия на практике приводят к расстройке системы, отклонению от расчетных режимов работы, ухудшению показателей качества управления, потере устойчивости. Например, при изменении коэффициента передачи процесса резания в 3 раза переходный процесс обычной САУ будет выглядеть так, как показано на рисунке. Видно, что система не может справиться с такимивозмущениями:  Рис.7 Переходной процесс при изменении коэффициента процесса резания Для обеспечения требуемых свойств системы необходимо синтезировать АдСУ, инвариантную к изменению коэффициента передачи объекта управления. Разработка структурной схемы АдСУ Инвариантность к изменению коэффициента передачи объекта управления можно обеспечить введением в основной контур управления сигнала, обратно пропорционального изменению этого коэффициента. Применим систему с эталонной моделью. По типу контура адаптации выбираем замкнутую систему. Так как математическая модель процесса точения известна, то адаптивная система управления должна приблизить движение реальной системы управления к движению «эталонной модели», т.е. выбирается адаптивная система управления с прямой адаптацией. По характеру настройки устройства управления основного контура выбираем самый простой тип адаптивной системы управления – самонастраивающуюся:  Рис.8 АдСУ с эталонной модель Моделирование АдСУ на ЭВМ Для моделирования работы АдСУ воспользуемся математическим пакетом Matlab. Структурная схема моделируемой системы показана на рис.9  Произведем анализ систем при изменении Кпр Кпр увеличим в 2 раза и получим переходные характеристики систем:  Рис. 10 Переходной процесс при Кпр увеличенном в 2 раза. 3)увеличим Кпр в 2,5 раза и снимем переходные характеристики  Рис. 11 Переходной процесс при Кпр увеличенном в 2,5 раза 3)увеличим Кпр в 10 раз  Рис. 12 Переходной процесс при Кпр увеличенном в 10 раз Произведем анализ систем при подаче синусоидального возмущения: При подаче синусоидального возмущения с такими параметрами, как амплитуда А=0.15; частота ω=0.5рад/с; с отклонением 1. Получим следующие переходные процессы  Рис.13 Системы с параметрами А=0.15, ω=0.5рад/с, отклонение 1 Увеличим амплитуду до А=0.5, отклонение 2 и частоту до ω=1 рад/с получим:  Рис.14 Системы с параметрами А=0.5, ω=1 рад/с, отклонение 2. Система при параметрах амплитуда А=1, частота ω=0.8 рад/с, и отклонение 5  Рис.15 Системы с параметрами А=1, ω=0.8 рад/с, отклонение 5. При значительном увеличении частоты до ω=5 рад/с, с периодом 0.628 сек - АдСУ «не успевает» подстраиваться к изменению объекта управления  Рис.15 Системы с параметрами А=1, ω=5 рад/с, отклонение 5. Заключение В ходе выполнения курсовой работы была синтезирована адаптивная система управления температурой в зоне резания по изменению коэффициента передачи процесса резания, были получены и закреплены практические навыки по анализу и составлению математических моделей объектов управления (процесс резания). Приобретен опыт моделирования и анализа АдСУ с помощью пакета прикладных программ Matlab. Список использованной литературы 1. Коуров Г.Н. ЗориктуевВ.Ц. Шарипов Б.У. Методические указания к курсовой работе по дисциплине “Теория управления”. 2. Бесекерский В.А. Руководство по проектированию систем автоматического управления. Москва “Высшая школа”, 1983г. 3.Лютов А.Г. Курс лекций ИСПУ |
