Анализ резистивных цепей постоянного тока

• Название: Анализ резистивных цепей постоянного тока
• Дата: 02.02.2019
• Размер: 42.62 Kb.
• Имя файла: 2.docx
• Тип: Анализ; #66127

Анализ резистивных цепей постоянного тока

Для схемы, соответствующей номеру варианта, выполнить:

1. Записать уравнения по законам Кирхгофа. Решив полученную систему уравнений, определить токи и напряжения ветвей.

2. Составить узловые уравнения цепи в матричной форме. Решив составленные уравнения, рассчитать токи во всех ветвях исходной цепи.

3. Составить расширенные узловые уравнения.

4. Результаты расчетов свести в таблицу.

5. Рассчитать ток в ветви с резистором 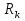методом эквивалентного генератора.

6. Определить, при каком сопротивлении резистора в нем выделяется максимальная мощность.

7. Построить графики зависимостей тока, напряжения и мощности, выделяемой в резисторе 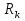при изменении сопротивления от 0.1 до 10 опт

Примечание: коэффициент усиления управляемого источника K =1

Параметр источника тока, управляемого током (ИТУН) S = 0.1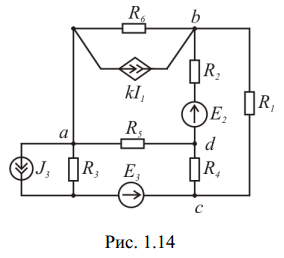





Рекомендации по выполнению расчетного задания

1. Последовательное соединение резистора и источника напряжения следует рассматривать как одну ветвь.

2. Схемы для всех вариантов имеют примерно одинаковую сложность. Для всех схем достаточно составить три уравнения по первому закону Кирхгофа и три – по второму.

3. При составлении уравнений по методу узловых напряжений источники напряжения следует преобразовать в эквивалентные источники тока.

4. При выполнении п. 5 (расчет методом эквивалентного генератора) следует помнить, что в цепи с управляемыми источниками входное сопротивление можно найти только как отношение напряжения холостого хода к току короткого замыкания. Напряжение холостого хода можно найти из системы узловых уравнений, полагая проводимость первого резистора равной нулю: G1= 0. Ток короткого замыкания легко найти, решив систему уравнений по законам Кирхгофа (п. 1 расчетного задания). В этой системе следует принять R1= 0. В этом случае ток короткого замыкания )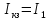

Требования к оформлению расчетного задания

1. Процесс решения должен сопровождаться краткими пояснениями.

2. Необходимо сначала записывать уравнения в символьном виде, а затем – в числовом.