дз тоэ. Анализ резистивных цепей

• Название: Анализ резистивных цепей
• Дата: 20.01.2022
• Размер: 456 Kb.
• Имя файла: дз тоэ.doc
• Тип: Закон; #337267

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ЦЕПЕЙ.

АНАЛИЗ РЕЗИСТИВНЫХ ЦЕПЕЙ
1.1.1. Используя законы Кирхгофа и Ома, определить ток i_k, напряжение u_k и мощность р_k каждого элемента цепи (_k — номер элемента).

Цепь: 113 – ИН u₁ = 1; 212 –R₂ =2; 332 – ИНu₃ = 5; 431 – ИТ i₄ = 1.
В соответствии с заданием составляем расчетную схему цепи.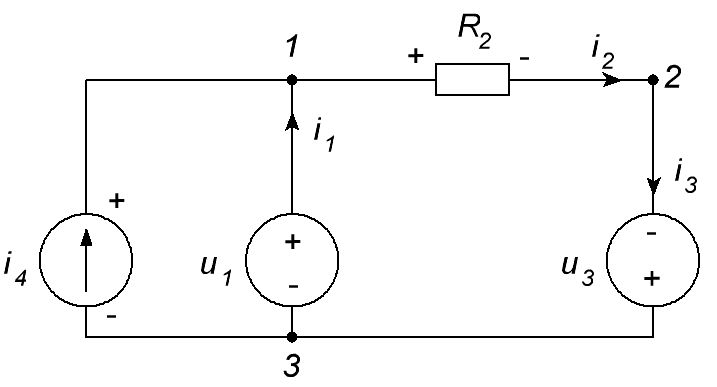



Задаем направления токов через элементы цепи. Рассчитываем значения токов.

Источник тока i₄ включен параллельно с источником напряжения u₁, поэтому .

По 2-му закону Кирхгофа определяем токи: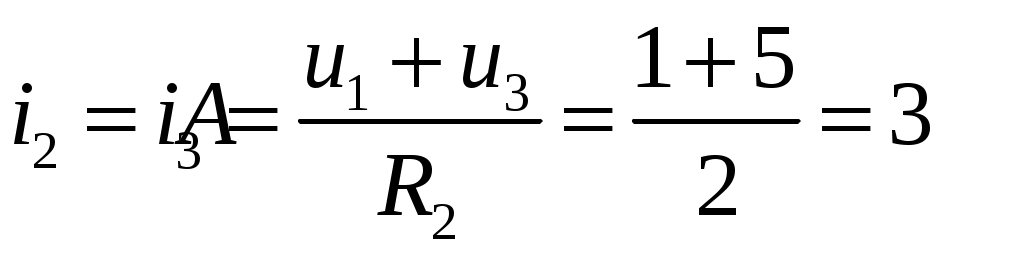

По 1-му закону Кирхгофа определяем ток:

Напряжение на сопротивлении :

Рассчитываем мощности на элементах цепи.

Для сопротивления R₂ направления напряжения и тока согласованы. Мощность этого элемента:

Для источников напряжения u₁, u₃ и источника тока i₄ направления напряжения и тока не согласованы. Мощности этих элементов



При p_k<0 элемент генерирует энергию, при p_k>0 элемент потребляет энергию.

Баланс мощностей:

Баланс мощностей выполняется.

1.1.2. Найти входное сопротивление цепи R_вх и указанные реакции, используя ФДН или ФДТ.

Цепь: 131 – ИТ i₁ = 5; 213 – R₂; 312 – R₃; 423 – R₄; 523 – R₅; R_к=2.

Найти i_k по ФДТ.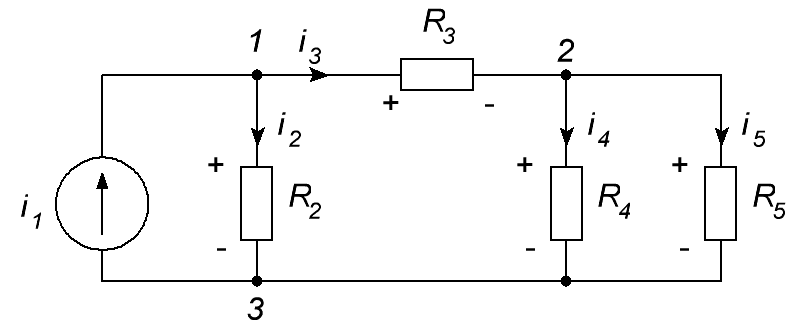


Рассчитываем входное сопротивление цепи.

Сопротивления R₄ и R₅ включены параллельно и последовательно с ними включено сопротивление R₃. Эквивалентное сопротивление этого участка: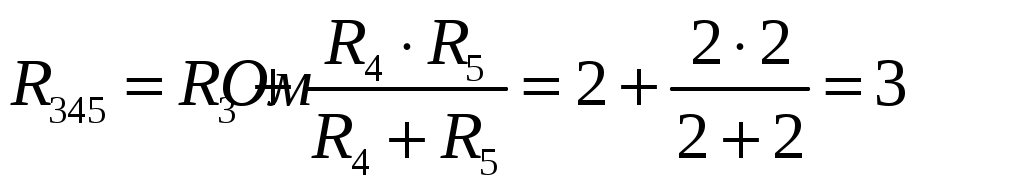

Исходную схему можем представить в виде: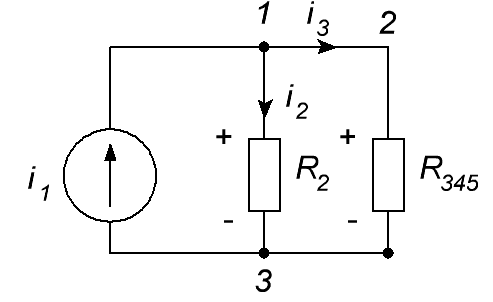



По этой схеме, по формуле ФДТ (формула делителя тока), определяем: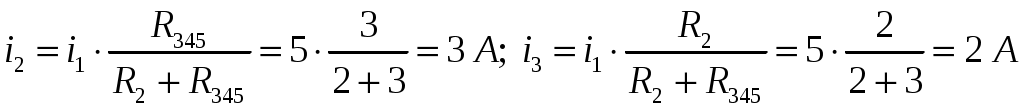



Рассчитываем остальные токи через сопротивления исходной схемы: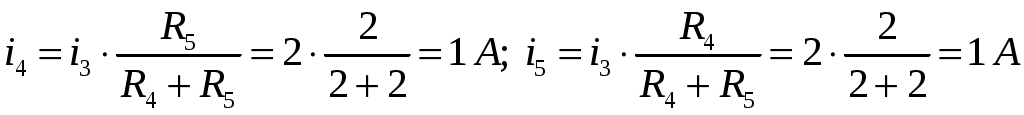



1.1.4. Методом пропорциональных величин найти i₅, u₃, G_вх, G_5–1, H_U3–1

Цепь: 114 – ИН u₁ = 120; 212 –R₂; 324 –R₃; 423 –R₄; 534 –R₅;

R_к=2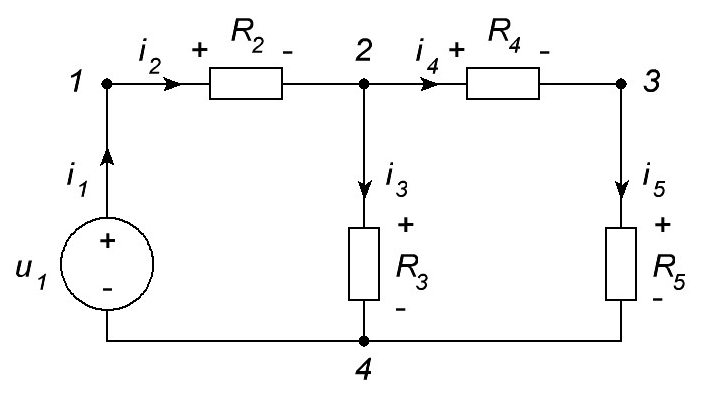


Задаем значение тока 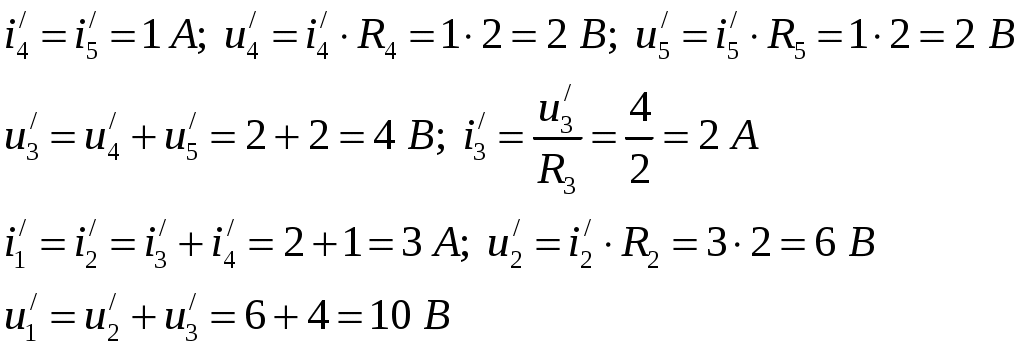и при этом значении, по законам Кирхгофа, рассчитываем остальные параметры цепи.



Определяем значение коэффициента пересчета: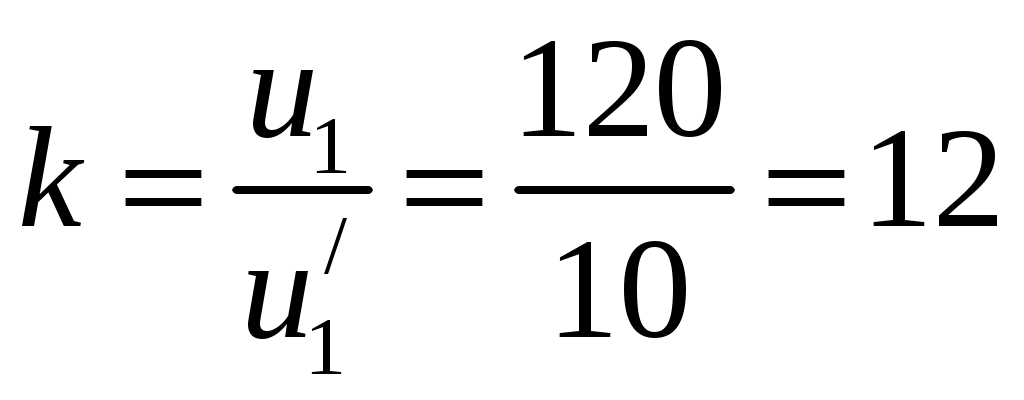

По известному значению коэффициента пересчета определяем действительные значения заданных параметров: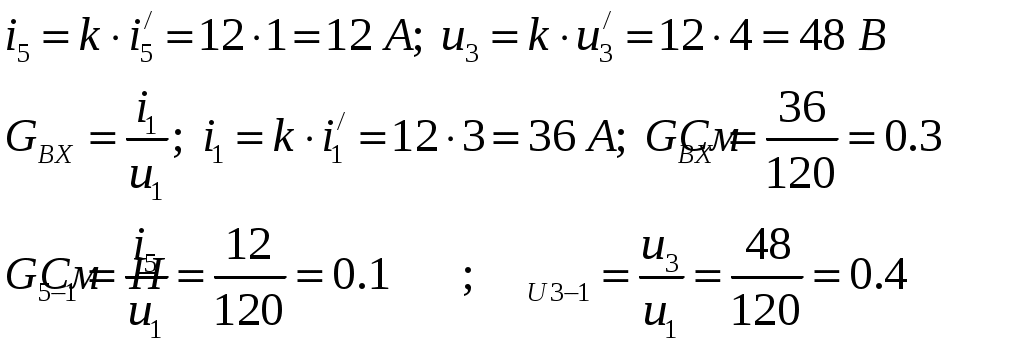



1.1.6. Составить уравнения MKT и МУН, считая все R_k = 2. Найти требуемую ре акцию.

Цепь: 115 – ИН u₁ = 2; 212 – R₂; 324 – ИН u_{3 =} 2; 413 – ИТ i₄ = 2; 535 – R₅; 634 – R₆; 754 – ИТ i₇ = 2; 845 – R₈; Найти i₂.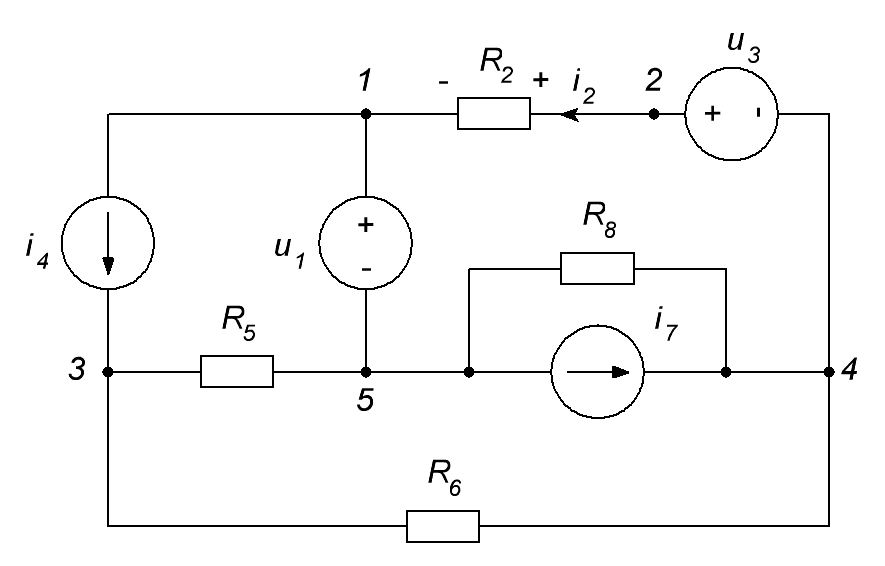


Для упрощения расчетов произведем преобразование исходной схемы. Преобразовываем источник тока i₇ в эквивалентный источник напряжения: 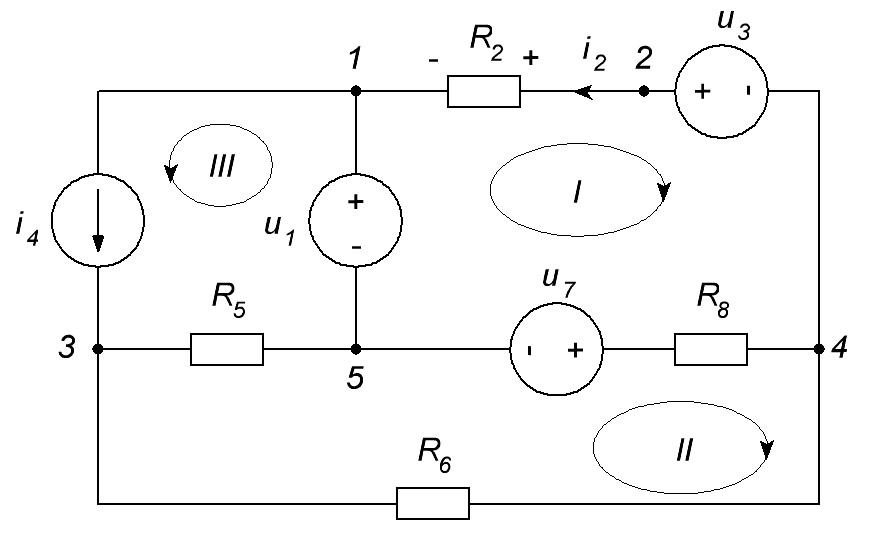. Исходная схема принимает вид:



1. Расчет методом контурных токов (МКТ).

Задаем на преобразованной схеме контура I, II, III и обозначаем для них контурные токи как 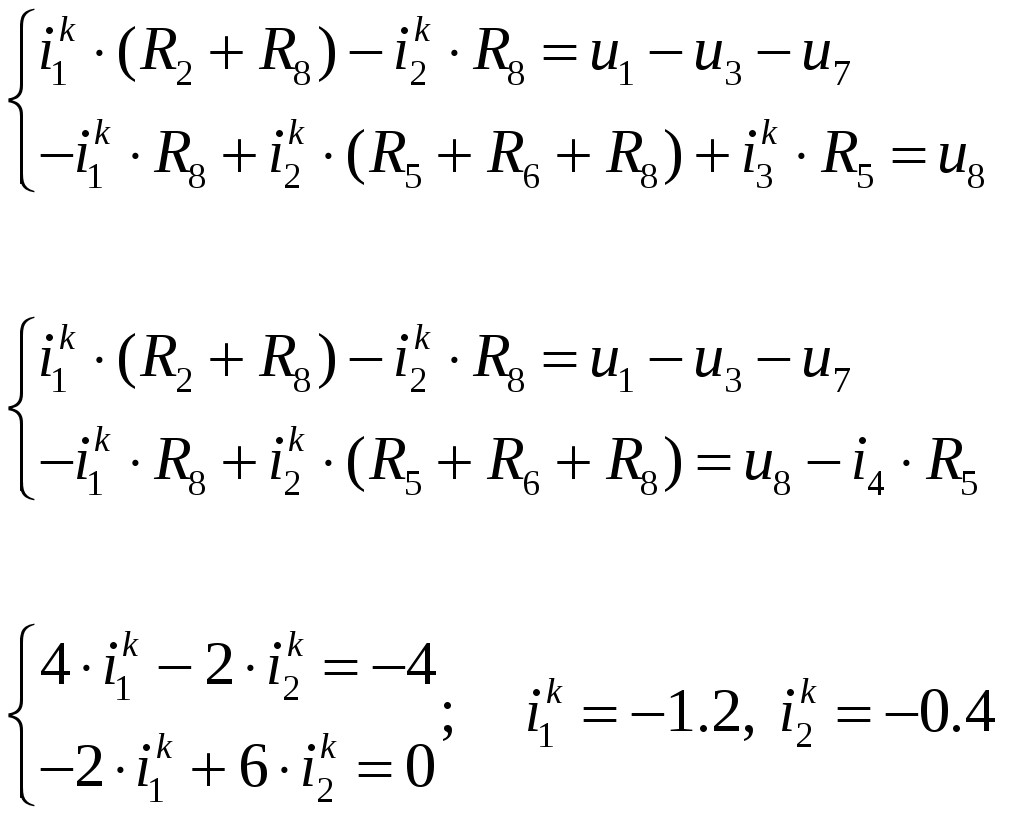. При этом, значение контурного тока . Следовательно, имеется 2 неизвестных контурных тока. Для их расчета составляем и решаем систему уравнений:



Соответственно, значение искомого тока:


2. Расчет методом узловых напряжений (МУН).

В преобразованной схеме принимаем значение потенциала узла 5 равным нулю ( ). Тогда, значение потенциала узла 1: .

Рассчитываем значения потенциалов узлов 3 и 4. Составляем и решаем систему по методу узловых потенциалов.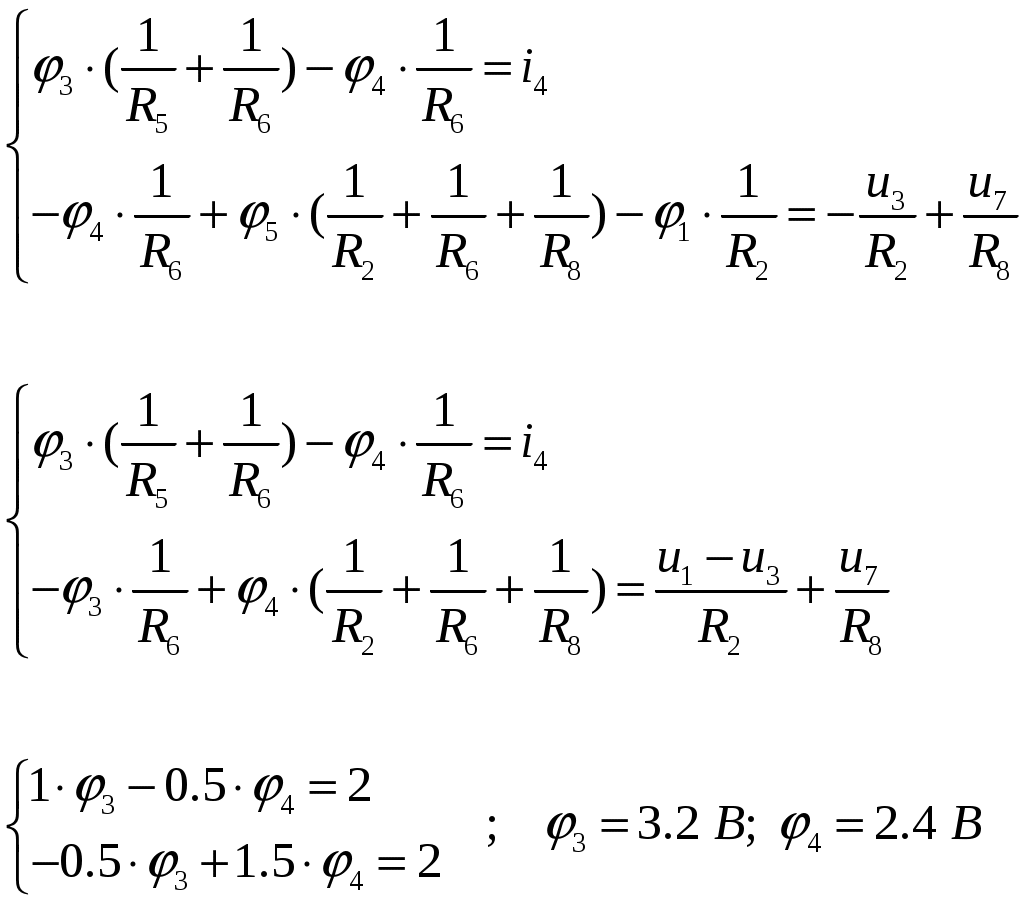



Соответственно, значение искомого тока: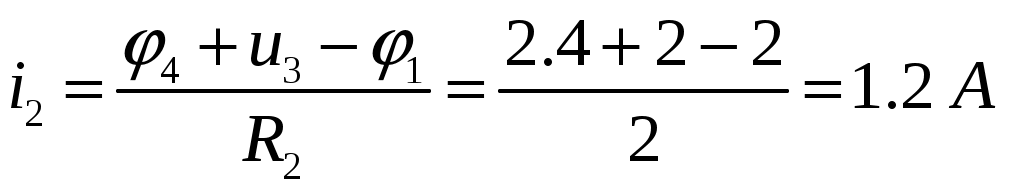

При расчете двумя методами получены одинаковые значения тока.

1.1.7. Используя методы эквивалентных источников (и МЭИН, и МЭИТ), определить указанную реакцию цепи.

Цепь: 114 – ИН u₁ = 7; 212 – R₂ = 1; 323 – R₃ = 3; 413 – ИТ i₄ = 1; 524 – R₅ = 3; 634 – R₆ = 3; Найти i₂.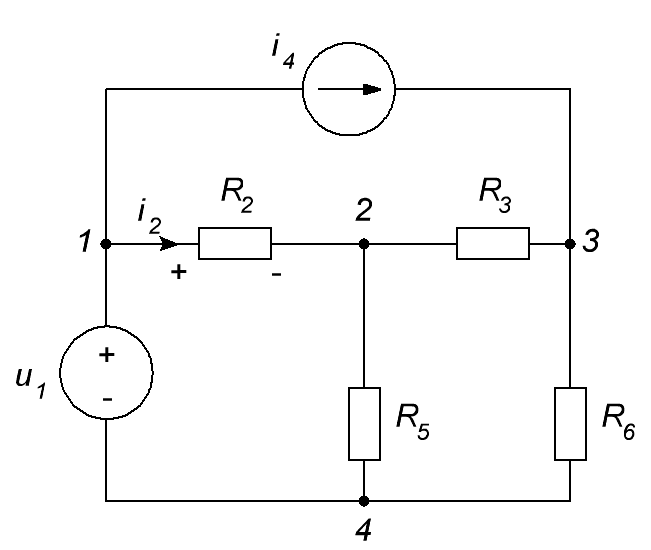


1. Расчет методом эквивалентного источника напряжения (МЭИН).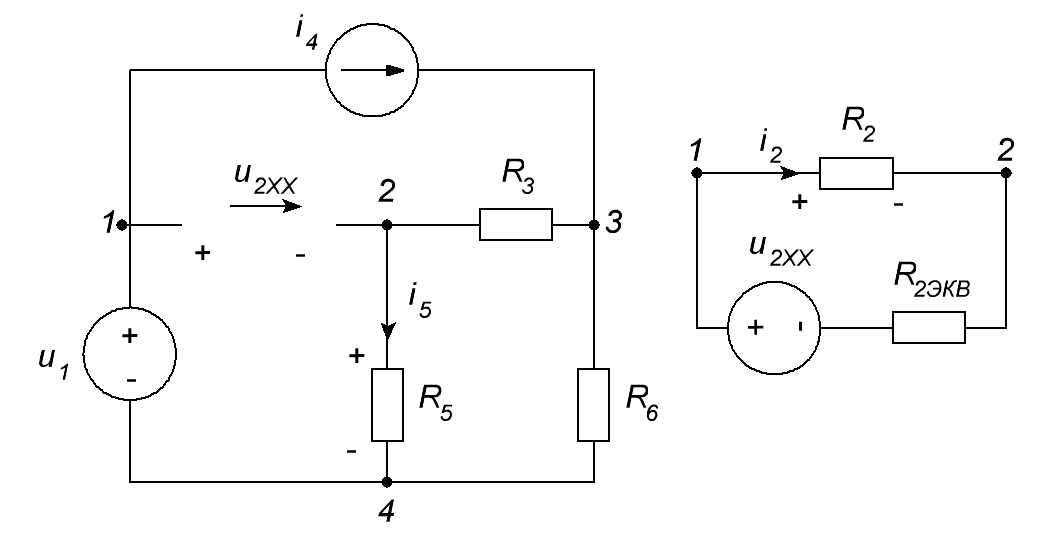



Рассчитываем напряжение холостого хода для сопротивления R₂: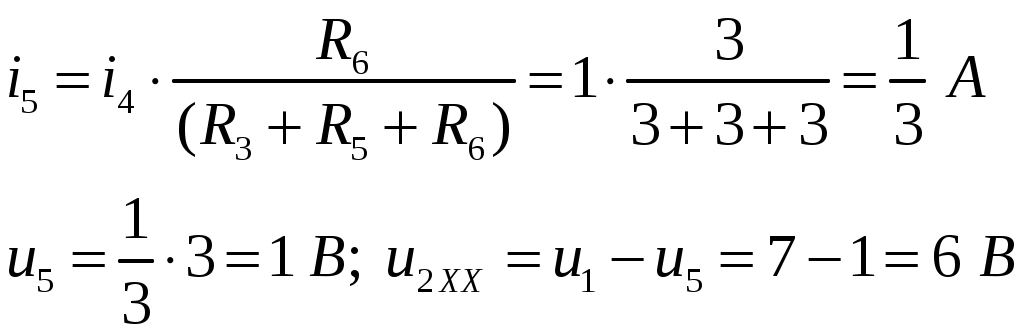



Рассчитываем эквивалентное сопротивление цепи относительно сопротивления R₂: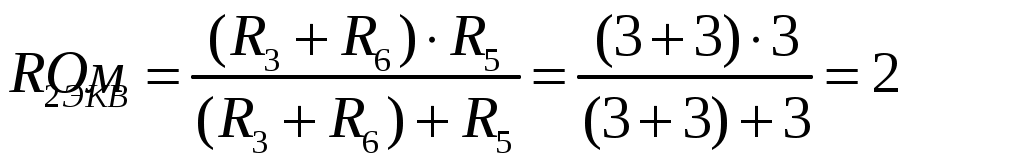
По полученной схеме эквивалентного источника определяем: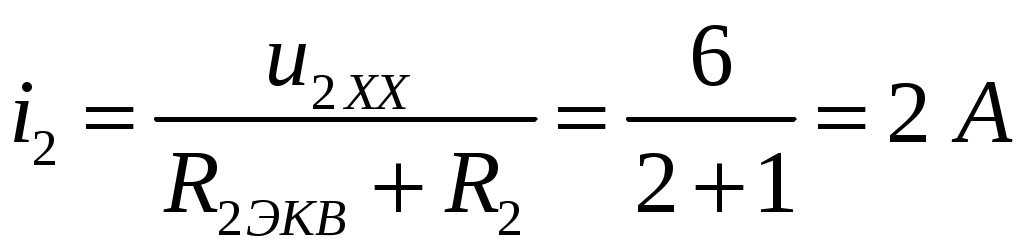



2. Расчет методом эквивалентного источника тока (МЭИТ).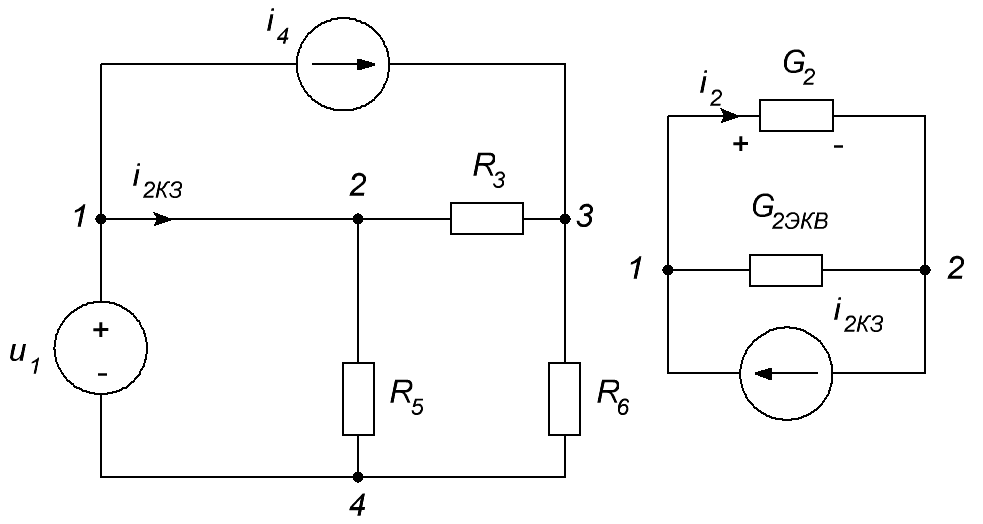



Рассчитываем ток короткого замыкания через сопротивление R₂: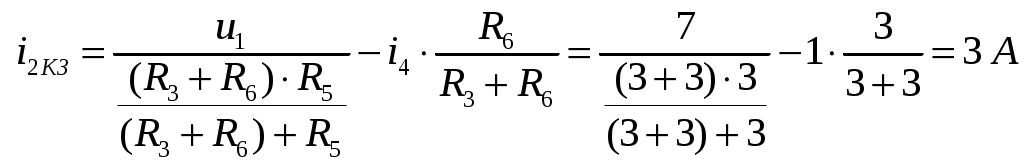



Рассчитываем эквивалентное сопротивление цепи относительно сопротивления R₂: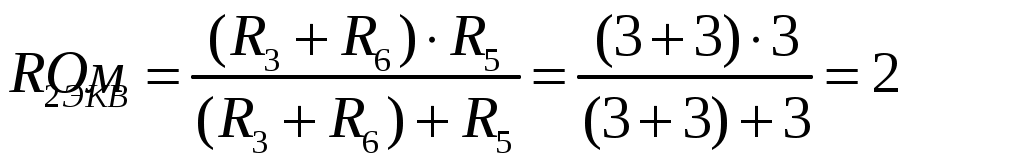

По полученной схеме эквивалентного источника определяем: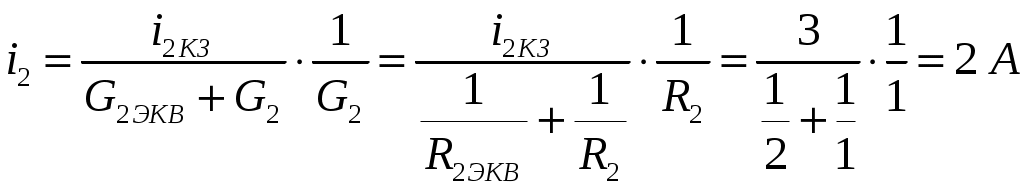



1.2.2. В момент t = 0 в цепи замыкается (размыкается) ключ К. Определить неза висимые начальные условия и найти для указанной реакции f₂ (0+), f_2в, f₂(t) при t > 0; построить график f ₂ (t).
Цепь: 116 – ИНu₁ = 24; 212 – R₂= 2; 324 –R₃ =2; 423 – L₄ = 3;535 –R₅ =2;

665 – ИН u₆ = 12; 746 – К, Замыкается. Найти u_3.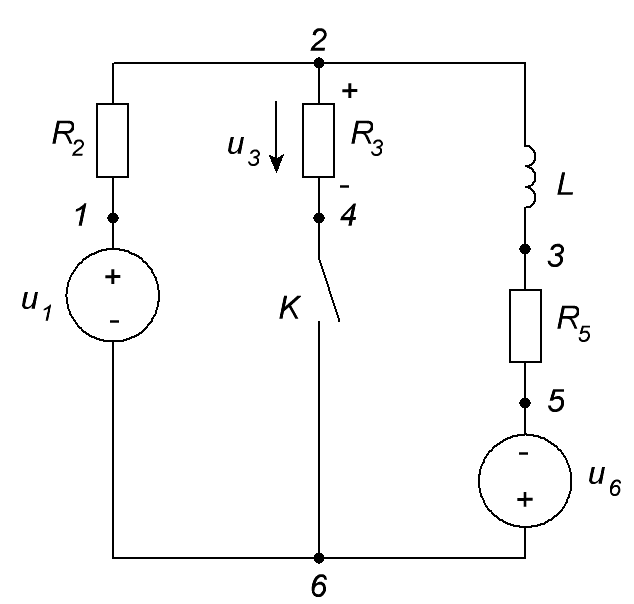



Рисунок 1. Заданная схема цепи.

Так как воздействия в цепи постоянны, то для анализа можно использовать схемы замещения.

1. Определяем независимые начальные условия, т.е. .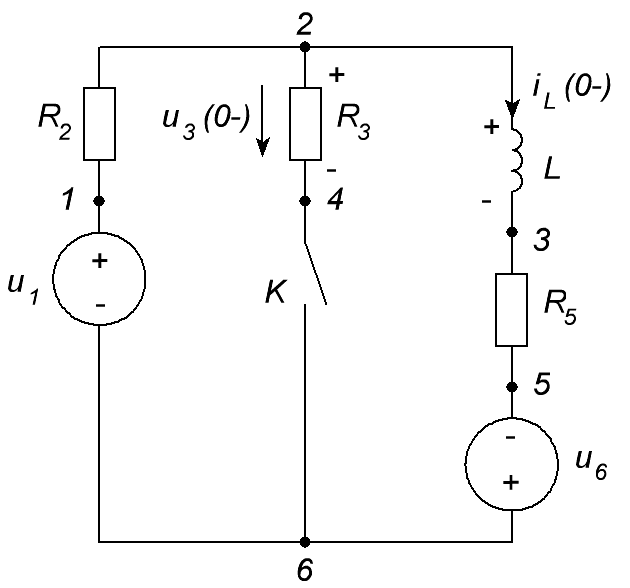



Рисунок 2. Схема замещения для расчета независимого начального условия.

По 2-му закону Кирхгофа определяем: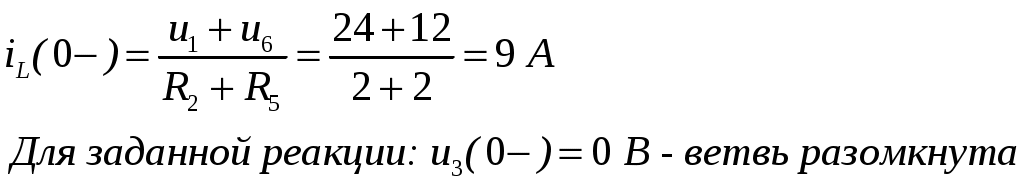



2. Находим вынужденные составляющие реакций. При постоянных воздействиях эти составляющие будут также постоянны (установившийся режим, t=∞). Используем схему замещения.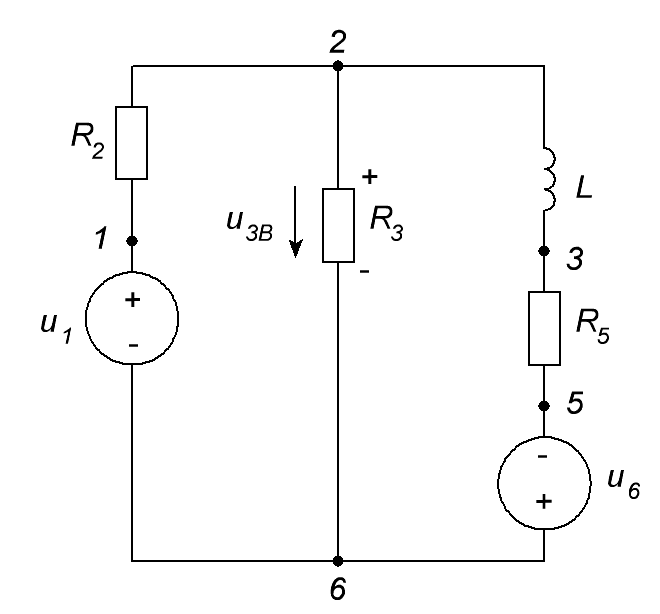



Рисунок 3. Схема замещения для расчета вынужденной составляющей реакции.
Для расчета используем метод двух узлов: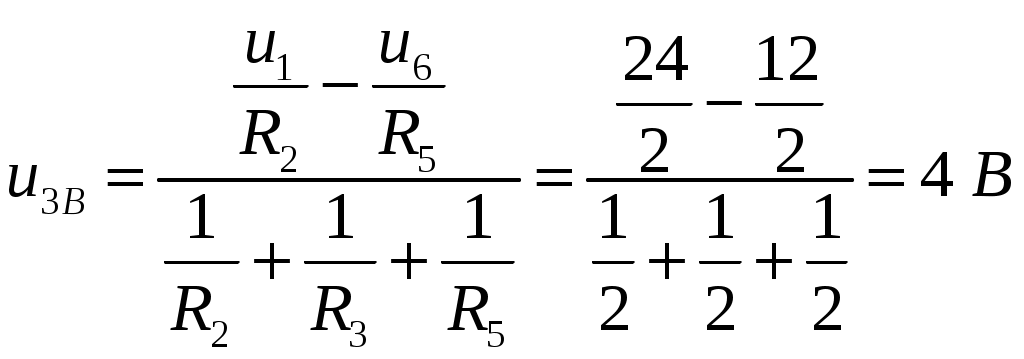



3. Находим зависимое начальное условие – значение заданной реакции в момент времени .

Составляем схему замещения, в которой вместо L-элемента исходной схемы включен ИТ .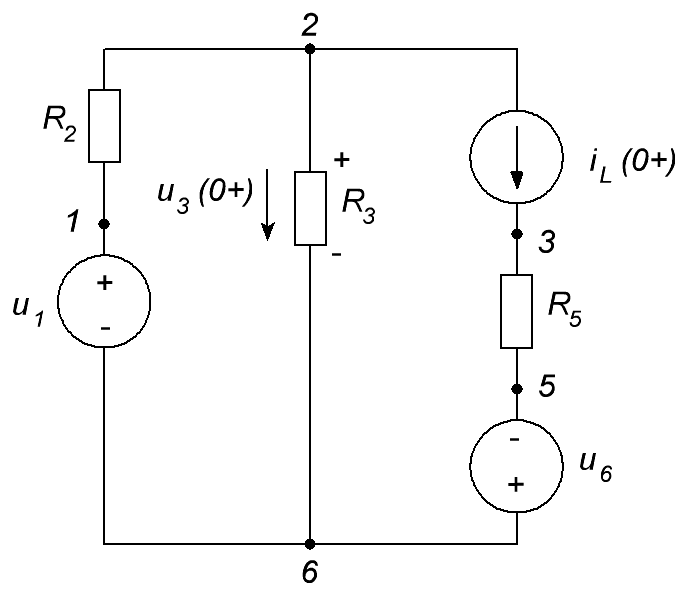



Рисунок 4. Схема замещения для расчета зависимого начального условия реакции.
Для расчета используем метод двух узлов: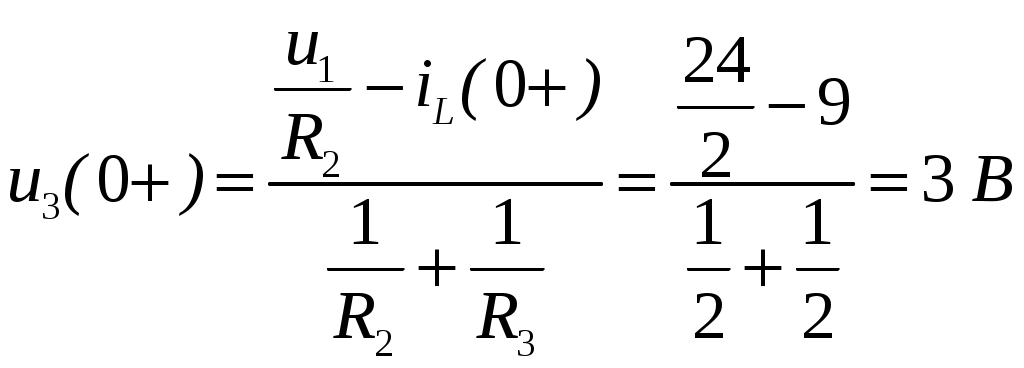


4. Определяем постоянную времени цепи, для чего составляем схему замещения и по ней определяем эквивалентное сопротивление цепи относительно катушки индуктивности: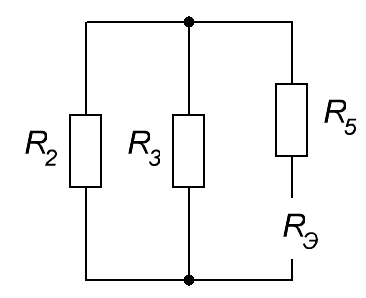



Рисунок 5. Схема замещения для расчета эквивалентного сопротивления постоянной времени.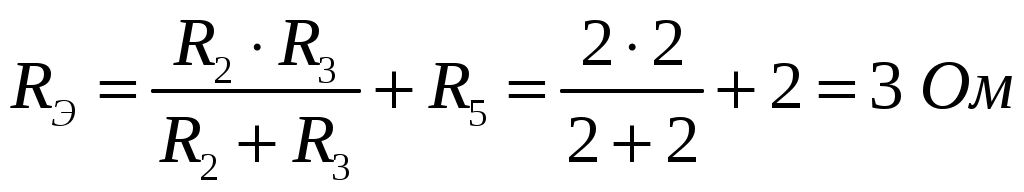


Постоянная времени: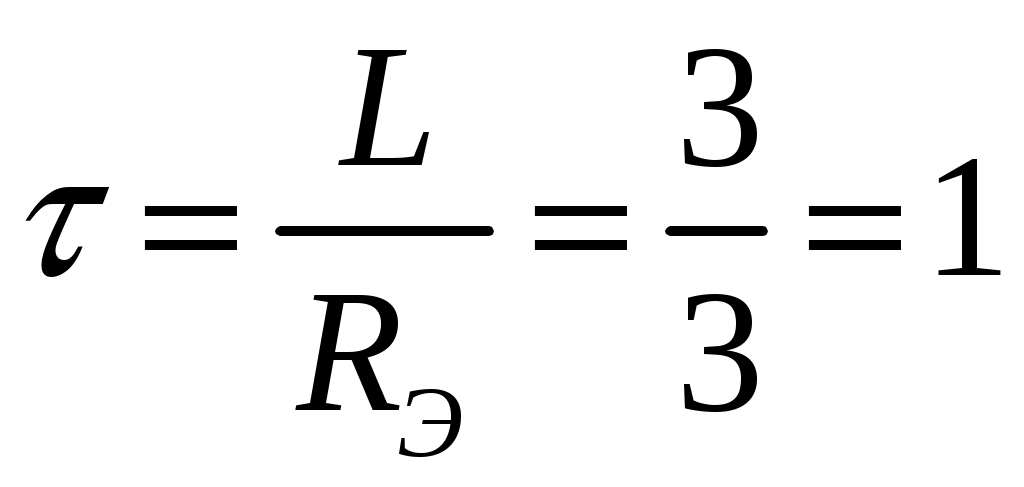

5. Выражение заданной реакции при переходном процессе представляем как сумму вынужденной и свободной составляющих.



Постоянную интегрирования находим по начальным условиям:

.

Таким образом, получаем выражение для заданной реакции:



По этому выражению строим график заданной реакции.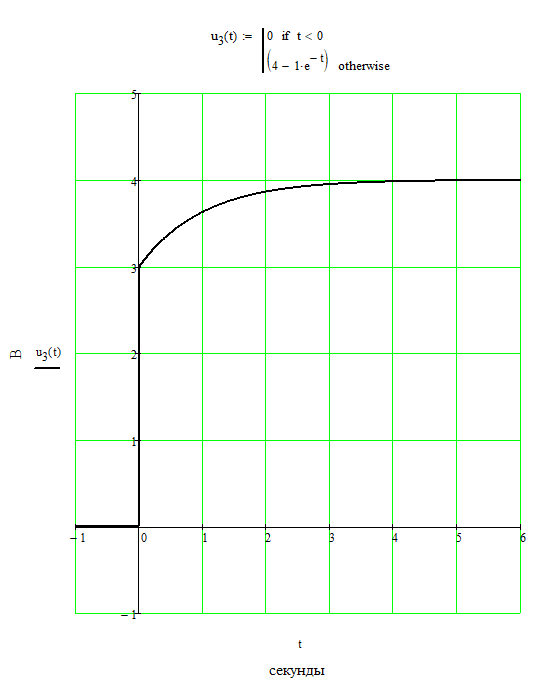



Рисунок 6. График заданной реакции u₃.

1.2.3. При t = 0 в цепи замыкается (размыкается) ключ К. Найти независимые начальные условия, составить уравнения состояния. Для t > 0 найти и_C и i_L использовав аналитическое решение уравнений состояния, а также численное — по методу Эйлера. Затем найти u_L и i_C, использовав уравнения связи, и провести проверку полученных результатов (по ВАХ накопителей).
Цепь: 115 – ИНu₁ = 6; 212 – R₂= 1;323 – R₃= 1; 435 –L = 1;

524 –K, размыкается;654 – R₆= 1; 725 – C= 1; 825 – ИТi₈ =3._.

1. По заданным параметрам составляем расчетную схему цепи.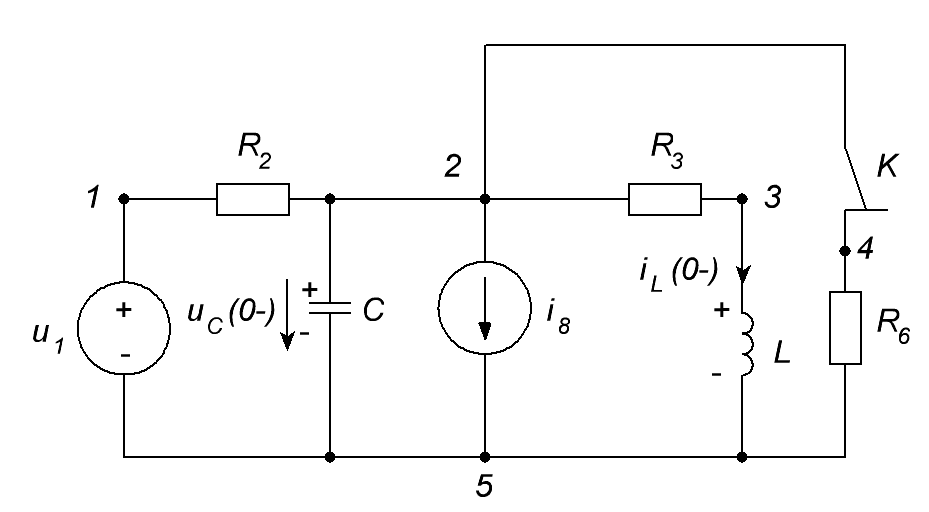



Рисунок 1. Заданная схема цепи.
2. Определяем независимые начальные условия – напряжение на конденсаторе и ток через катушку в режиме до коммутации (размыкания ключа). По методу двух узлов рассчитываем: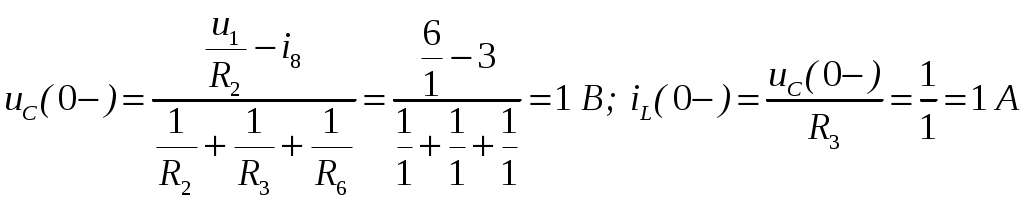

.

3. Для цепи после коммутации составляем систему дифференциальных уравнений, описывающих состояние цепи.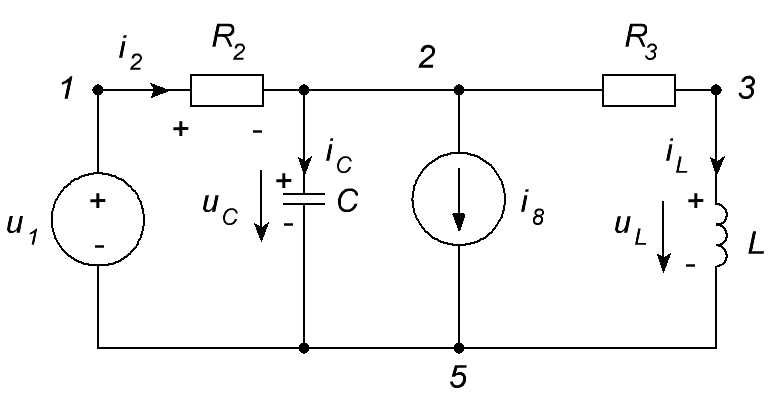



Рисунок 2. Схема цепи после коммутации.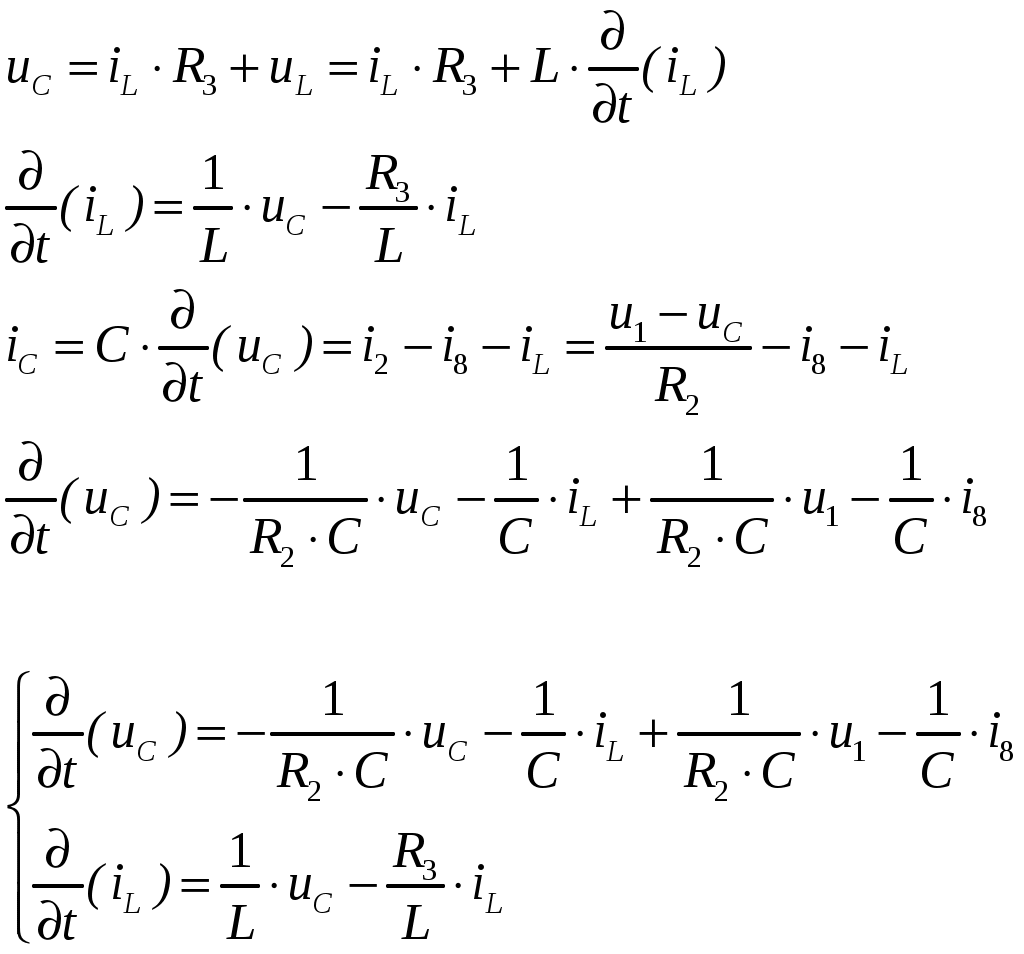



После постановки числовых значений, получаем: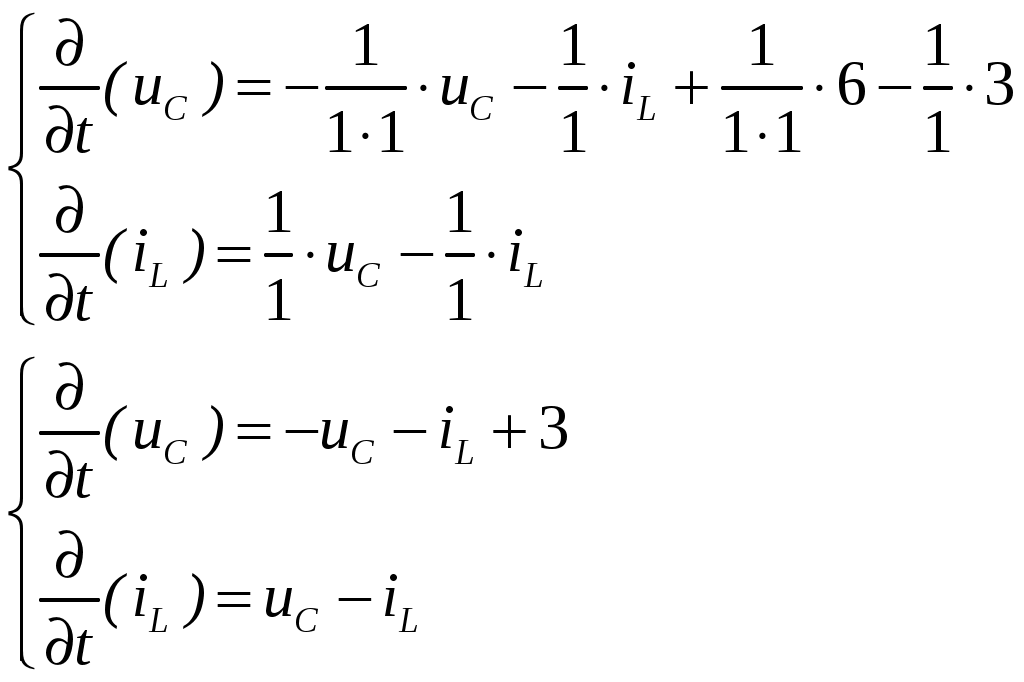



По полученной системе составляем и решаем характеристическое уравнение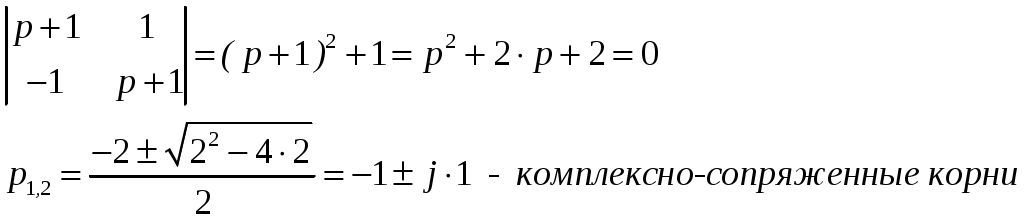



4. Так как получены комплексно-сопряженные корни, то законы изменения тока катушки и напряжения конденсатора будем искать в виде: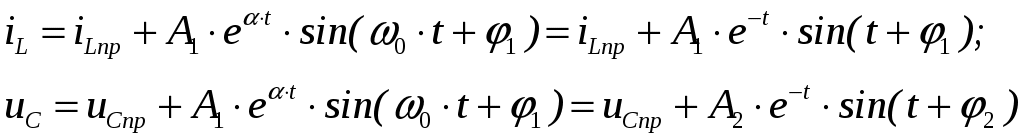



5. Определяем принужденные составляющие – параметры цепи в установившемся режиме после коммутации.

По методу двух узлов определяем: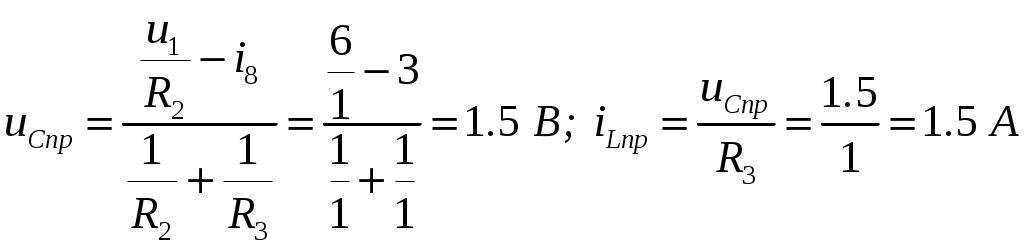



6. Расчет постоянных интегрирования производим исходя из параметров цепи в момент коммутации t=0.

Расчет тока катушки индуктивности.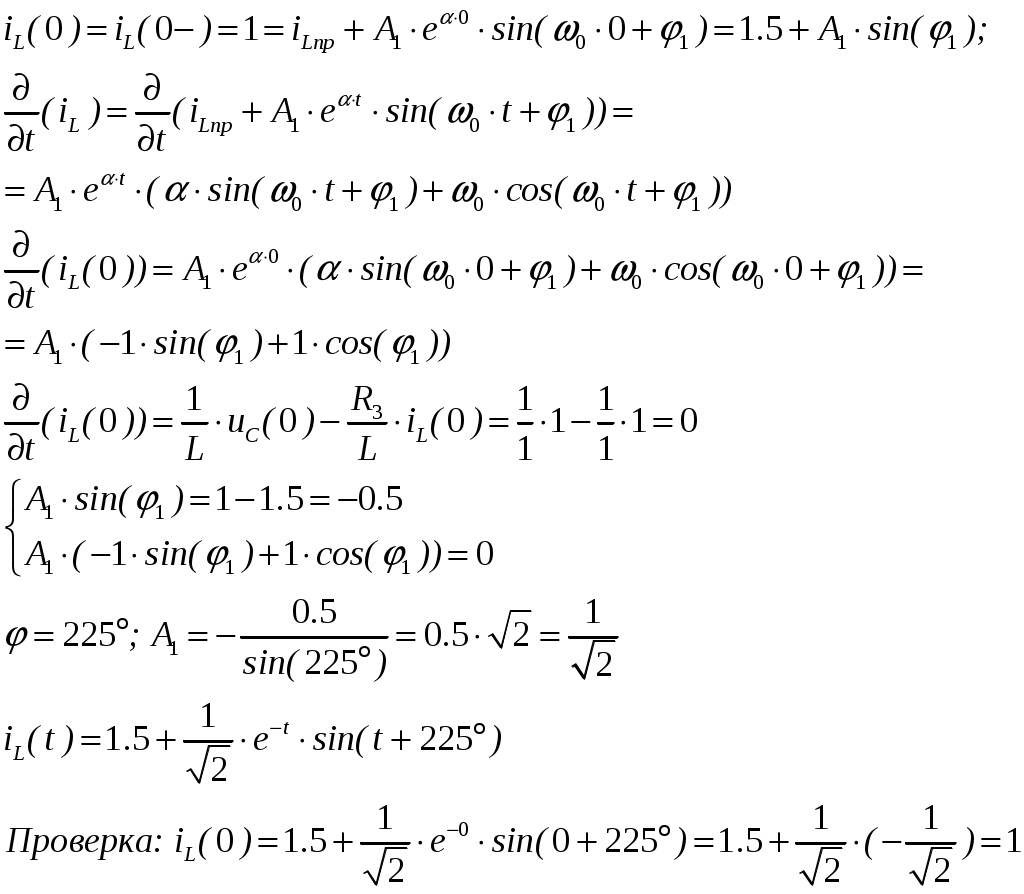



Расчет напряжения конденсатора.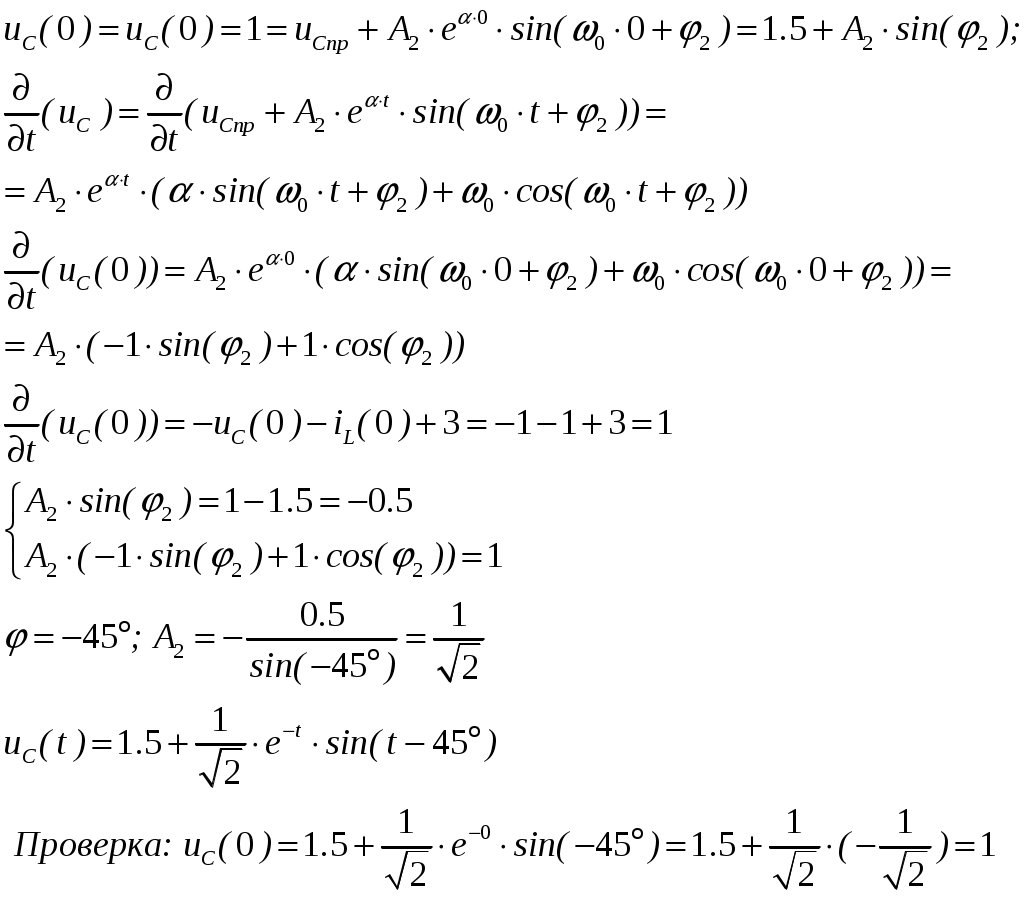



Численное решение по методу Эйлера производим с помощью ПЭВМ в программе MathCad.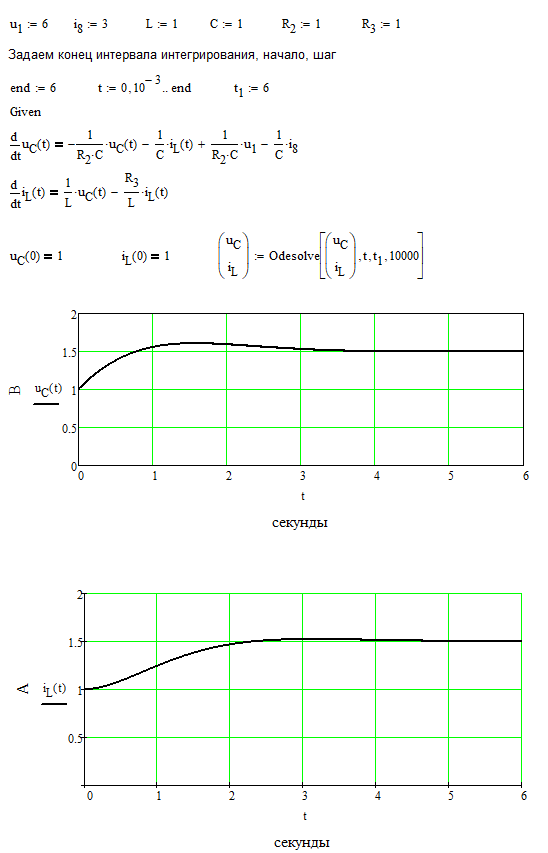



Рисунок 3. Графики напряжения конденсатора и тока катушки полученные по методу Эйлера.

7. Используя уравнения связи находим законы изменения напряжения катушки и тока конденсатора.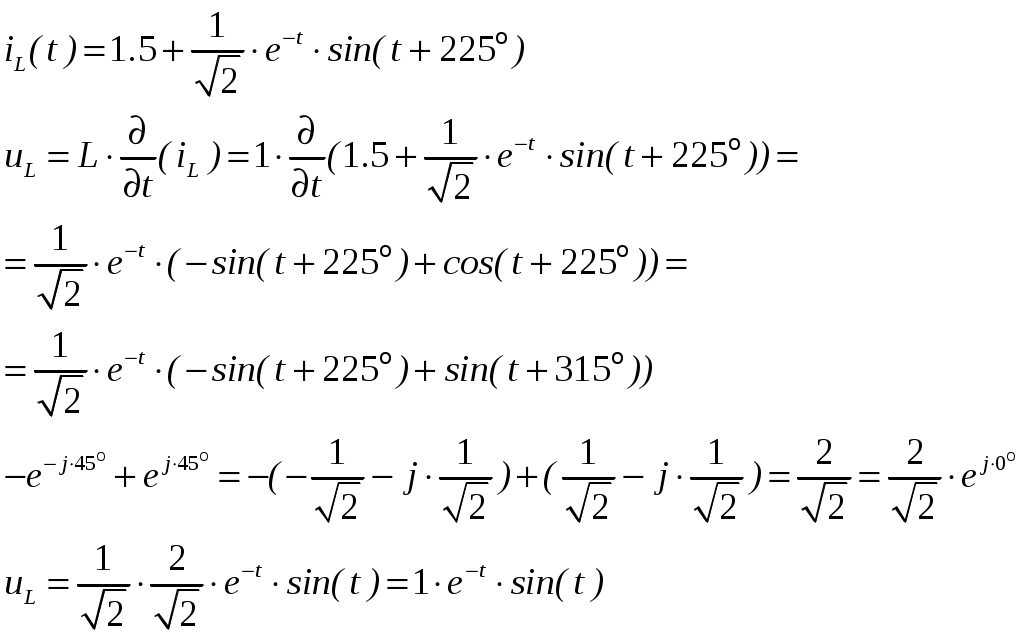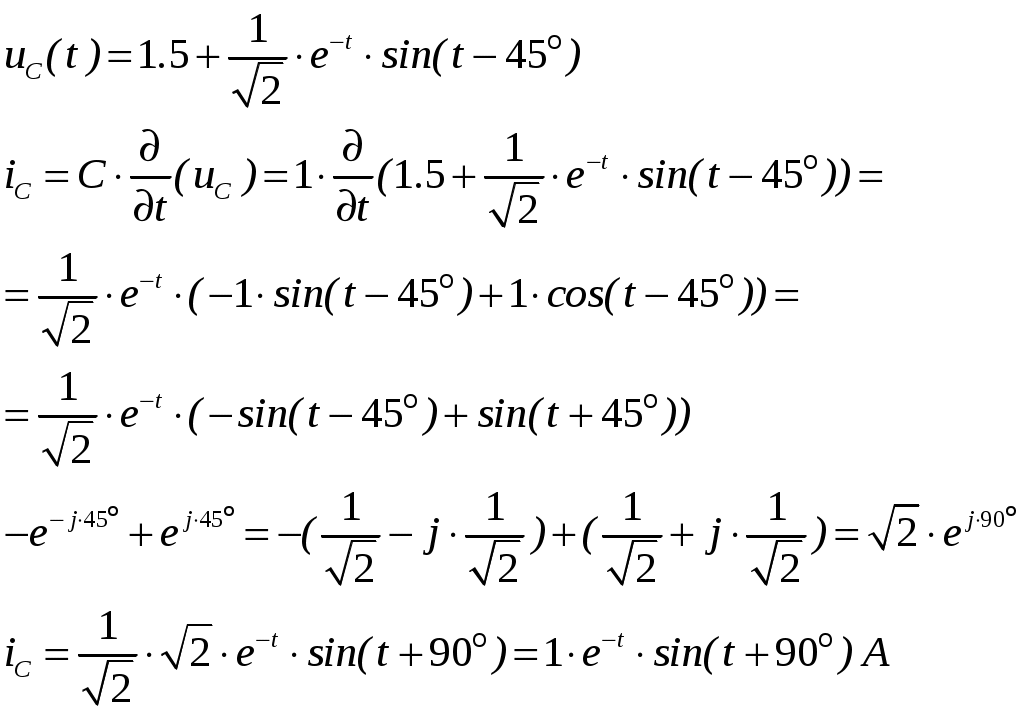





Производим проверку полученных результатов: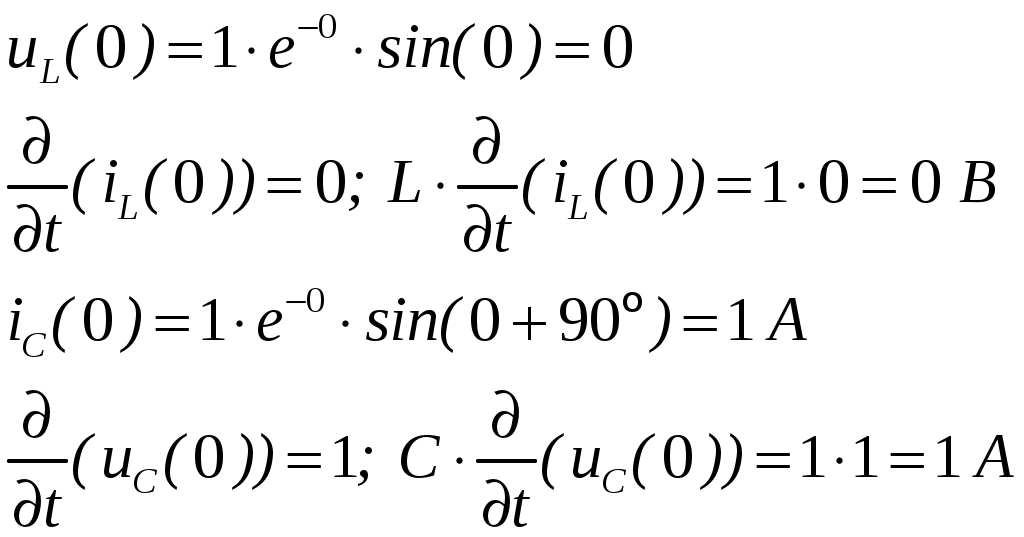



Строим графики изменения во времени рассчитанных параметров: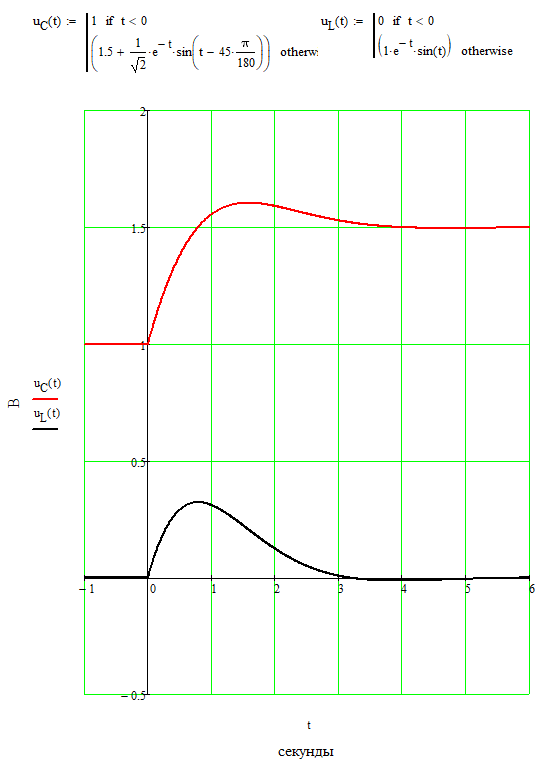



Рисунок 4. Графики напряжений конденсатора и катушки полученные по методу переменных состояния.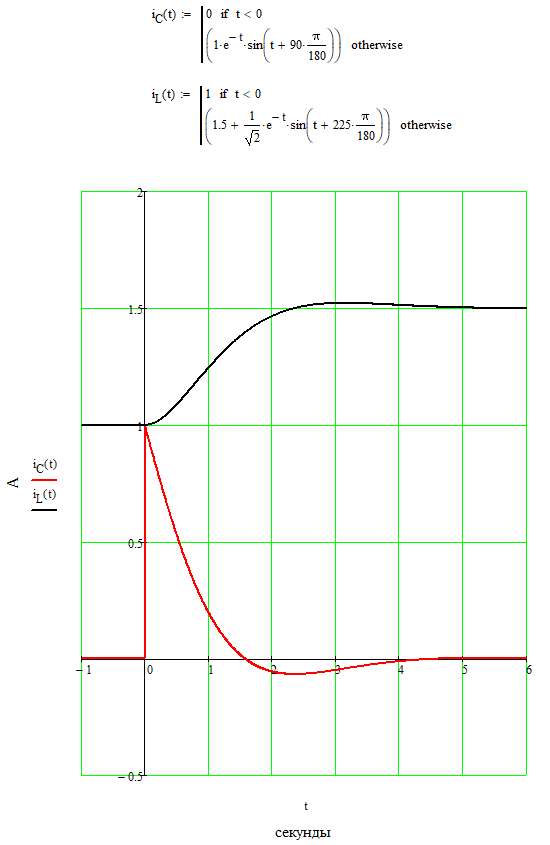



Рисунок 4. Графики токов конденсатора и катушки полученные по методу переменных состояния.