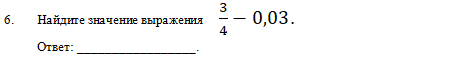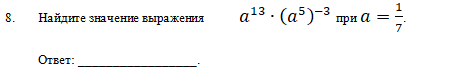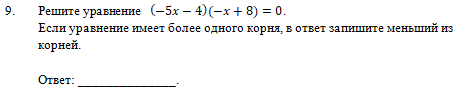|
|
Методический анализ РПР-1_2022. Анализ результатов региональной проверочной работы по математике в 9 классе i этап 24 ноября 2021 год
I этап – 24 ноября 2021 года
Назначение КИМ РПР – оценить уровень общеобразовательной подготовки по математике обучающихся IX классов общеобразовательных организаций в целях подготовки к государственной итоговой аттестации выпускников. Результаты РПР могут быть использованы для адресной поддержки обучающихся при подготовке к ГИА 9.
РПР проводятся в соответствии с приказом министерства образования Саратовской области № 1843 от 10 ноября 2021 года «Об организации и проведении региональных проверочных работ по математике для обучающихся 9 классов общеобразовательных организаций Саратовской области 2021/2022 учебном году».
Документы, определяющие содержание КИМ
Содержание проверочной работы определяется на основе Федерального государственного образовательного стандарта основного общего образования (приказ Министерства образования и науки РФ от 17.12.2010 № 1897) с учётом Примерной основной образовательной программы основного общего образования (одобрена решением Федерального учебно-методического объединения по общему образованию (протокол от 8.04.2015 № 1/15)).
Подходы к отбору содержания, разработке структуры КИМ
Содержание проверочной работы приближено к содержанию КИМ ОГЭ в рамках базового уровня математической подготовки и фактического материала, который изучен обучающимися на момент проведения проверочной работы.
Структура КИМ ОГЭ отвечает цели построения системы дифференцированного обучения математике в современной школе. Дифференциация обучения направлена на решение двух задач: формирования у всех обучающихся базовой математической подготовки, составляющей функциональную основу общего образования, и одновременного создания условий, способствующих получению частью обучающихся подготовки повышенного уровня, достаточной для активного использования математики во время дальнейшего обучения.
КИМ разработаны с учётом положения о том, что результатом освоения основной образовательной программы основного общего образования должна стать математическая компетентность выпускников, т.е. они должны: овладеть специфическими для математики знаниями и видами деятельности; научиться преобразованию знания и его применению в учебных и внеучебных ситуациях; сформировать качества, присущие математическому мышлению, а также овладеть математической терминологией, ключевыми понятиями, методами и приёмами.
Характеристика структуры и содержания КИМ
Региональная проверочная работа содержит 19 заданий базового уровня сложности.
При проверке базовой математической компетентности обучающиеся должны продемонстрировать: владение основными алгоритмами; знание и понимание ключевых элементов содержания (математических понятий, их свойств, приемов решения задач и проч.); умение пользоваться математической записью, применять знания к решению математических задач, не сводящихся к прямому применению алгоритма, а также применять математические знания в простейших практических ситуациях.
Каждое задание базового уровня характеризуется пятью параметрами: элемент содержания, проверяемое умение, категория познавательной области, уровень трудности, форма ответа. В КИМ предусмотрены следующие формы заданий: с выбором ответа из четырех предложенных вариантов, с кратким ответом, на соотнесение. Верный ответ на задание базового уровня оценивался 1 баллом.
Распределение заданий КИМ по содержанию, проверяемым умениям и способам деятельности
В проверочной работе содержатся задания по всем ключевым разделам математики, отраженным в кодификаторе элементов содержания (КЭС). Количество заданий по каждому из разделов кодификатора примерно соответствует удельному весу этого раздела в курсе. Распределение заданий по разделам содержания приведено в таблице 1.
Таблица1.Распределениезаданийпоразделамсодержаниякурсаматематики
Код по КЭС
|
Название раздела
|
Количество заданий
|
1
|
Числа и вычисления
|
7
|
2
|
Алгебраические выражения
|
1
|
3
|
Уравнения и неравенства
|
2
|
4
|
Числовые последовательности
|
1
|
5
|
Функции и графики
|
1
|
6
|
Координаты на прямой и плоскости
|
1
|
7
|
Геометрия
|
5
|
8
|
Статистика и теория вероятностей
|
1
|
Ориентировочная доля заданий, относящихся к каждому из разделов кодификатора требований (КТ), представлена в таблице 2.
Таблица2.Распределение заданийпопроверяемымумениямиспособамдействий
Код по КТ
|
Основные умения и способы действий
|
Количество заданий
|
1
|
Уметь выполнять вычисления и преобразования
|
2
|
2
|
Уметь выполнять преобразования алгебраических выражений
|
1
|
3
|
Уметь решать уравнения, неравенства и их системы
|
2
|
4
|
Уметь строить и читать графики функций
|
1
|
5
|
Уметь выполнять действия с геометрическими фигурами, координатами и векторами
|
4
|
6
|
Уметь работать со статистической информацией, находить частоту и вероятность случайного события
|
1
|
7
|
Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели
|
8
|
Результаты выполнения заданий
19заданийпо всем ключевым разделам курса математики основной школы, отраженным в кодификатореэлементовсодержания(КЭС), соответствующих уровню базовой подготовки обучающихся.
В таблице 3. приведены в сравнении результаты выполнения заданий по разделам содержания участниками региональной проверочной работы РПР-1 за 2020/2021 уч.г. и РПР-1 за 2021/2022 уч.г.
Таблица 3
№ п/п
|
Основные проверяемые требования к математической подготовке
|
Коды поверяемых элементов содержания
|
Коды разделов элементов требований
|
Средний процент выполнения (РПР-1 2020/2021 уч.г.)
|
Средний процент выполнения (РПР-1 2021/2022 уч.г.)
|
1.
|
Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели.
|
1–8
|
1, 7
|
91,59
|
87,99
|
2.
|
Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели.
|
1–8
|
1, 7
|
58,84
|
52,03
|
3.
|
Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели.
|
1–8
|
1, 7
|
61,68
|
36,88
|
4.
|
Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели.
|
1–8
|
1, 7
|
39,63
|
43,79
|
5.
|
Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели.
|
1–8
|
1, 7
|
22,77
|
29,91
|
6.
|
Уметь выполнять вычисления и преобразования
|
1
|
1
|
60,99
|
66,45
|
7.
|
Уметь выполнять вычисления и преобразования
|
1, 6
|
1
|
72,95
|
72,99
|
8.
|
Уметь выполнять вычисления и преобразования, уметь выполнять преобразования алгебраических выражений
|
1, 2
|
1, 2
|
64,62
|
39,95%
|
9.
|
Уметь решать уравнения, неравенства и их системы
|
3
|
3
|
38,88
|
41,53
|
10.
|
Уметь работать со статистической информацией, находить частоту и вероятность случайного события, уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели.
|
8
|
6, 7
|
49,91
|
54,02
|
11.
|
Уметь строить и читать графики функций
|
5
|
4
|
53,02
|
50,71
|
12.
|
Осуществлять практические расчеты по формулам; составлять несложные формулы, выражающие зависимости между величинами
|
2
|
7
|
41,26
|
26,35
|
13.
|
Уметь решать уравнения, неравенства и их системы
|
3, 6
|
3
|
43,45
|
45,99
|
14.
|
Уметь строить и читать графики функций, уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни, уметь стоить и исследовать простейшие математические модели
|
4
|
4, 7
|
54,45
|
43,66
|
15.
|
Уметь выполнять действия с геометрическими фигурами, координатами и векторами
|
7
|
5
|
65,34
|
65,06
|
16.
|
Уметь выполнять действия с геометрическими фигурами, координатами и векторами
|
7
|
5
|
26,61
|
33,52
|
17.
|
Уметь выполнять действия с геометрическими фигурами, координатами и векторами
|
7
|
5
|
33,95
|
35,09
|
18.
|
Уметь выполнять действия с геометрическими фигурами, координатами и векторами
|
7
|
5
|
57,24
|
26,95
|
19.
|
Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения
|
7
|
5
|
42,88
|
52,02
|
Предполагаемый процент выполнения заданий базового уровня сложности по спецификации ФИПИ колеблется от 60% до 90%. В этом учебном году в указанный диапазон попали только 4 задания, в прошлом учебном году таких заданий было 6.
Общие результаты
Общие результаты, полученные участниками РПР-1, представлены в таблице 4.
Таблица 4
Всего в РПР-1 участвовали
|
19152 обучающихся
|
19 баллов (максимальный результат)
|
197 обучающихся (1,03 %)
|
18 баллов
|
401 обучающихся (2,09 %)
|
Все 5 заданий по геометрии выполнили неверно (задания 15–19)
|
3767 обучающихся (19,67 %)
|
Выполнили неверно все задания с 1 по 14
|
368 обучающихся (1,92 %)
|
Содержательный анализ выполнения заданий КИМ Анализ результатов выполняемости заданий РПР-1 показал, что наибольшие затруднения у обучающихся вызвали задачи 1 – 5 объединенные практико-ориентированным контекстом. Причем сложности при выполнении этих заданий возникли у обучающихся, получивших разные отметки. В вариантах РПР обучающимся были предложены задачи практико-ориентированного блока объединенные контекстом «Домохозяйство». Выполнение задач требовало от обучающихся наличия способности применять освоенные математические знания и умения при решении реальных ситуаций. 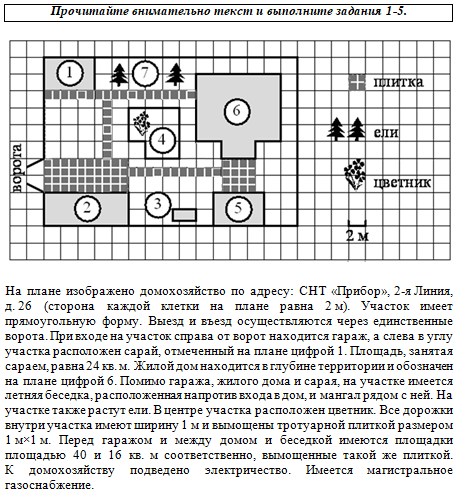
Так, например, для выполнения первого задания обучающимся необходимо было найти нужную информацию в тексте, сопоставить с планом и внести в таблицу. В бланк ответов нужно было перенести последовательность четырех цифр без пробелов, запятых и других дополнительных символов. Для получения балла за выполнение задания №1 обучающиеся должны были продемонстрировать навыки смыслового чтения и аккуратно заполнить бланк ответов. И 87,99% справились с этим заданием. 
Следующие три задания требовали выполнения арифметических действий с натуральными числами и десятичными дробями, но числовые данные также требовалось извлечь из предложенного текста и плана.
В задании №2 нужно было определить площадь одного из объектов на плане. Если сопоставив текст с планом объект определен верно, то при вычислении величины площади надо было не упустить информацию о масштабе. Задание на подсчёт квадратиков на плане. Внимательное чтение условия – оценка размера квадратика на плане – вывод, что площадь одного квадратика – 4м2. Площадь необходимо было найти в квадратных метрах, но в бланк вписать только число. 
Задание №3 – задание на подсчёт квадратиков (и плиток) на плане. Внимательное чтение условия – сопоставление размера квадратика на плане и размера плитки – вывод, что один квадратик покрывают четыре плитки. Деление с округлением до целого числа с избытком. Определив количество упаковок в бланк вписать только число. 
В задании №4 надо было определить процент площади занимаемой определенным объектом. Проценты, площадь, масштаб; и снова нужно использовать информацию с плана. Определив нужную часть площади в процентах в бланк вписать только число.  Именно эти три возможных балла и потеряла основная масса девятиклассников: запутались в вычислениях, не учли масштаб, неверно округлили или не нашли нужные числовые данные в тексте или на плане.
В задании №5 нужно было построить математическую модель реальной ситуации. Просчитав затраты для двух предложенных в условии вариантов выбрать оптимальный, а потом, опираясь на сделанный выбор, ответить на главный вопрос задачи. 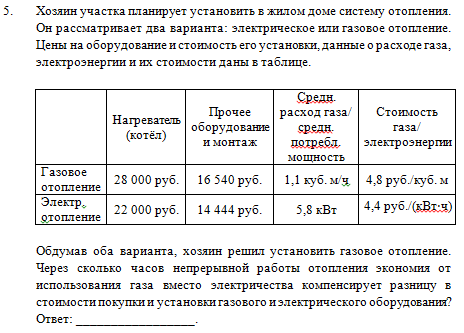 Потерю баллов в пятом задании можно объяснить непониманием условия задачи, вычислительными ошибками при осуществлении действий с целыми числами и десятичными дробями, еще обучающиеся могли запутаться в единицах измерения величин. Кроме того некоторые обучающиеся вообще не приступали к решению этого задания, пропустив его как «сложное с большим текстом и длинными вычислениями». Для того чтобы обучающиеся успешно справлялись с подобными заданиями полезно научить их прежде, чем приступить к непосредственному решению, выделять в тексте требования задания (основной вопрос), выделять формулы, которые понадобятся для решения, если они указаны в тексте, или найти их в справочных материалах; оценить правдоподобность получившегося результата, делать проверку и т.п. С этой целью можно включить в содержание обучения задания, требованием которых будет: «найдите в тексте …», «выпишите формулы, которые потребуются для решения задачи …», «составьте план действий при решении задачи …», «спрогнозируйте возможный результат и объясните свой прогноз» и т.п. Кроме того, необходимо в процессе обучения сделать акцент на смысловое чтение, несформированность которого негативно сказывается на результатах выполнения задания по математике. В задании №6 нужно было выполнить одно действие с дробями, причем обыкновенную дробь можно было перевести в десятичную и выполнить вычитание записывая числа в столбик. 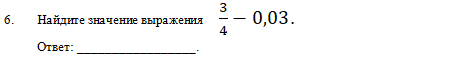 Не смотря на заложенную в задании легкость выполнения, с ним справились 66,45% участников РПР. Часть обучающихся допустили ошибку в вычислении (пробел в знаниях из Математики 5-6), а часть при записи полученного ответа 0,72 в клетки бланка, что свидетельствует о недостаточной осведомленности участников РПР о правилах заполнения бланков.
В задании №7 нужно было определить координату точки на прямой, выбрать один из четырех предложенных ответов, причем в бланк ответов надо было внести номер выбранного ответа. С этим заданием успешно справились 72,99% участников РПР. 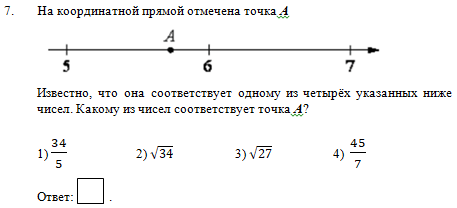
Задание №8 относится к теме «Преобразования алгебраических выражений». Для нахождения значения выражения сначала нужно было преобразовать это выражение, используя свойства степени, и только потом подставлять значения переменной в полученное выражение – при таком способе решения риск допустить вычислительную ошибку минимальный. При решении этого задания без предварительных преобразований прямой подстановкой могло привести к ошибкам вычислительного характера и как итог к неправильному ответу. В результате с этим заданием справились 39,95% 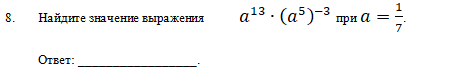
В задании №9 представлено уравнение вида «Произведение равно нулю». Этот вид одни из самых распространенных в математике уравнений. Их начинают изучать с 6 класса и там множители представляют собой линейные уравнения. К окончанию 9 класса обучающиеся освоят методы решения более сложных уравнений (квадратных, дробно-рациональных), но при этом многие из более сложных уравнений могут сводиться к уравнению вида «Произведение равно нулю» с линейными множителями. Именно поэтому в РПР было включено такое уравнение. Результат выполнения этого задания достаточно невысокий – 41,53%. 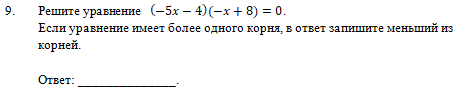 Единственная сложность в этом задании в том, что надо было записать в ответ меньший из найденных корней. Ошибки могли быть допущены при выполнении действий с отрицательными числами или при записи полученного ответа в клетки бланка. Для ответа «–0,8» надо занять 4 клетки: знак отрицательного числа «–» и разделитель целой и дробной части числи «,» каждый занимают по отдельной клеточке.
Задание №10 на нахождение вероятности случайного события. Ошибки, которые допускают обучающиеся при решении этого задания, в большинстве случаев происходят из-за невнимательного прочтения текста задания – находят вероятность противоположного события или записывают вероятность в виде процента, а не десятичной дроби. 54,02% участников РПР верно решили и правильно записали ответ в этом задании. 
В задании №11 нужно бы установить соответствие между графиками и формулами, которые их задают. В вариантах РПР были предложены графики и формулы линейных функций, т.к. этот материал на момент проведения РПР освоен обучающимися, не зависимо от учебника, по которому ведется обучение. При этом с заданием справились 50,71% участников РПР. 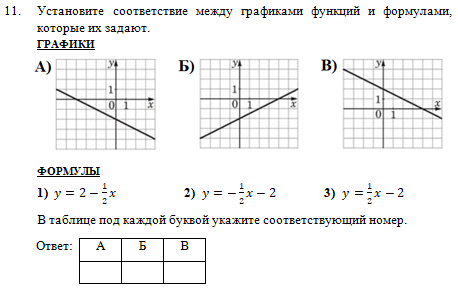
В задании №12 нужно было осуществить практические расчеты по представленной в условии формуле. В задании была достаточно простая формула, содержащая всего одно действие, но основную сложность в задании составил перевод вычисленной величины расстояния из сантиметров в километры. В итоге с этим практико-ориентированным заданием справились всего 26,35% участников РПР. 
В задании №13 нужно было из четырех решений выбрать соответствующее предложенному неравенству, а в ответ записать номер выбранного решения. С этим справились 45,99% участников РПР. 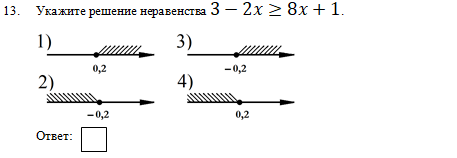
Задание №14 относится теме «Числовые последовательности. Прогрессии», которая еще не изучена обучающимися на момент написания РПР-1. Поэтому в вариант включено задание пропедевтического характера, для решения которого достаточно понимать описанную в условии ситуацию и вычислить последовательно все члены последовательности, а затем их сложить. Результат выполнения этого задания 43,66%. 
Для решения задания №15, относящегося к теме «Треугольники», нужно было воспользоваться свойством равнобедренного треугольника и теоремой о смежных углах, получить ответ в градусах, но знак градуса в клетки бланка ответов не вносить. С этим заданием справились 65,06% участников РПР. 
В задании №16, относящемуся к теме «Окружность и круг», надо было выполнить несложное дополнительное построение — радиус окружности (соединить центр окружности и конец хорды). Построенный отрезок является гипотенузой прямоугольного треугольника, длину которой можно найти по теореме Пифагора. Главная трудность этого задания оказалась не в геометрическом содержании, а в вычислениях квадратного корня из четырехзначного числа. С этим заданием справились 33,52% участников РПР. 
Для решения задания №17, относящегося к теме «Четырехугольники», нужно было воспользоваться формулой площади трапеции. Числовые данные для вычисления нужно было выбрать из избыточного количества представленного на рисунке. С заданием справились 35,09% участников РПР. 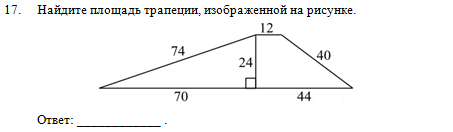
В задании №18 «Задача на клетчатой бумаге». Для решения необходимо было осуществить дополнительное построение: из вершины В опустить перпендикуляр на АС, а далее в полученном прямоугольном треугольнике посчитать по клеточкам длины катетов и вычислить тангенс острого угла С по формуле через длины катетов. С заданием справились 26,95% участников РПР. 
Выполнение задания №19 требовало от обучающихся теоретических знаний по всем темам, изученным на момент проведения РПР. Для успешного выполнения задания достаточно было внимательного прочтения предложенных утверждений и сопоставления с известными геометрическими фактами.  Уровень выполнения этого задания 52,02% при сравнении с более низкими процентами по заданиям 16, 17, 18 свидетельствует о том, что обучающиеся обладают теоретическими знаниями, но применяют их не достаточно уверенно. Как видно из содержания задач (15-19), для их выполнения требовалось только знание фактологического материала. В процессе обучения следует обратить внимание на знание обучающимися геометрических фактов, свойств геометрических фигур и определения понятий. Для этого полезно составлять памятки, ментальные карты, позволяющие визуализировать теоретический материал, проводить зачеты, ориентированные на систематизацию и закрепление теоретических знаний.
Выводы и рекомендации Таким образом, трудности при выполнении заданий по алгебре у обучающихся традиционно связаны с низким уровнем вычислительной культуры, что говорит о необходимости акцентировать на этом внимание учителей. Причем в большей степени это проявляется в заданиях, где вычислительные навыки являются средством, а не предметом контроля. При подготовке к ОГЭ по математике следует больше времени уделять отработке вычислительных навыков, включая соответствующие задания на различных этапах уроков. Анализ результатов выполнения заданий по геометрии показывает, что обучающиеся хуже справляются и с заданиями, в которых требуется применить какой-то известный факт (свойство, признак), формулу в определенной ситуации. Ошибки в основном связаны или с незнанием необходимых фактов, например, основных геометрических фигур и их свойств, или с неумением применять известные факты. Большинство из перечисленных выше ошибок и выявленных пробелов и проблем повторяется из года в год. С большей долей вероятности следует пересмотреть методику изучения соответствующих вопросов, возможно, она устарела, не учитывает особенности нового поколения. Необходимо также обратить внимание на организацию подготовки к успешной сдаче ОГЭ.
Устоявшиеся подходы в обучении математике, как показали результаты ОГЭ 2021, дают сбой и не позволяют обеспечить должного качества математической подготовки современных обучающихся. Акцентирование внимания в учебном процессе только на предметные результаты, оставляет «за бортом» такие важные навыки обучающихся как смысловое чтение, прогнозирование, организация собственной деятельности и др., несформированность которых мешает добиться желаемого результата. Учителям необходимо пересмотреть систему подготовки обучающихся, а также используемую ими методику обучения, изменить нигилистское отношение к актуальным образовательным результатам. Следует снизить уровень академичности на уроках математики, активнее включать в содержание обучения математике практико-ориентированные задания, моделировать ситуации, позволяющие обучающимся освоить навыки применения математических знаний и умений при решении проблем, возникающих в реальной жизни.
|
|
|
 Скачать 271.11 Kb.
Скачать 271.11 Kb.