Анализ российского рынка ноутбуков на декабрь 2009года
 Скачать 358 Kb.
|
|
Московский государственный институт международных отношений (университет) МИД РФ Кафедра эконометрики и математических методов анализа экономики Информационно-аналитическая справка на тему «Анализ российского рынка ноутбуков на декабрь 2009года» Выполнили студентки III курса факультета МЭО 4 ак. группы Бойко Е.И. Мошкина Ю.О. Научный руководитель: Сернова Н.В. Москва 2009 Содержание Введение 3 Анализ данных. Корреляционный анализ 4 Регрессионный анализ. Условия Гаусса-Маркова 6 Анализ качества модели 8 Фиктивные переменные 13 Заключение 14 Приложения 16 ВведениеВ бизнесе, экономике, общественных науках, исследовании экономической активности и даже исследовании политических процессов для анализа процессов и их прогнозирования широко используются математические модели. Модель, построенная и верифицированная на основе уже имеющихся наблюдений, может быть использована для прогноза значений зависимой переменной в будущем или для других наборов значений объясняющих переменных. Целью нашего исследования является нахождение зависимости цены на ноутбуки на Российском рынке на декабрь 2009 года от некоторых факторов. В связи со значительным ростом рынка ноутбуков в последние годы, появлением большого количества различных моделей и марок данного товара, чрезвычайно важно знать от каких факторов в большей степени зависит цена, так как она является сильно дифференцированной. Также данное исследование полезно для розничных сетей по продаже ноутбуков, поскольку облегчает задачу установления цены на товар. В нашем исследовании мы учли наиболее важные факторы, которые могут повлиять на цену. Во-первых, это физические характеристики ноутбука: размеры (диагональ) и вес, ведь логично было бы предположить, что цена прямо зависит от диагонали и имеет обратную зависимость по отношению к весу. Из технических характеристик мы учитываем память RAM, так как от нее зависит быстродействие компьютера, следовательно, цена должна находиться от нее в прямой зависимости. К тому же мы вводим ряд фиктивных переменных. Во-первых, это наличие или отсутствие процессора Core 2 Duo, что может существенно повлиять на цену. В-вторых, с помощью фиктивных переменных мы учитываем значение бренда компании. Для исследования были взяты 4 наиболее популярных в России бренда: HP, Toshiba, Acer и Asus. Анализ данных. Корреляционный анализДля проведения исследования соберем данные по ноутбукам и оформим их в таблицу (приложение 1). Обозначим цену на компьютеры как y, x1 – память (RAM), x2 – вес ноутбука, x3 – диагональ. d1 – фиктивная переменная, равная 1 при наличии процессора Core 2 Duo и нулю при его отсутствии. R1, R2 и R3 – также фиктивные переменные, указывающие на бренд производителя. R1 равен 1 у компьютеров марки HP, R2 – Toshiba и R3 – Acer (включение в модель фиктивных переменных рассмотрено в отдельной главе). Построим графики корреляционного поля (геометрическое место точек, координаты которых соответствует паре чисел x и y) для каждой из переменных. Так же построим линию тренда (приложение 2) Так как из графиков 1, 2 и 3 приложения 2 видно, что тренд имеет форму прямой во всех 3 случаях, мы можем принять гипотезу о наличии линейной зависимости между переменными y, x1, x2, x3. Вычислим показатель тесноты корреляционной зависимости (линейный коэффициент корреляции) для каждого x. Он рассчитывается по формуле:  . Так как  , а  , то  .Используем для расчетов коэффициентов корреляции в MSExcel функцию КОРРЕЛ() или в Eviews на панели управления выбираем View/Correlations. Таким образом получим r1=0,33, r2=0,37, r3=0,34. Все 3 показателя находятся в интервале (0; 0,5], это означает, что между y и рассматриваемыми факторами существует слабая прямая корреляционная зависимость. Проверим статистическую значимость выборочных коэффициентов корреляции. Докажем, можно ли судить на основе выборки о свойствах генеральной совокупности, то есть являются ли выборочные показатели существенными и значимыми для принятия предположений о наличии данного свойства в генеральной совокупности. Примем гипотезу о том, что в генеральной совокупности нет корреляции при уровне значимости α=0,05 Ho: ρ=0 H1: ρ≠0 Гипотеза проверяется с помощью специального показателя, разработанного на основе выборки. Этот показатель называется статистическим критерием. Он вычисляется по формуле:  t является случайной величиной, имеющей распределение Стьюдента. 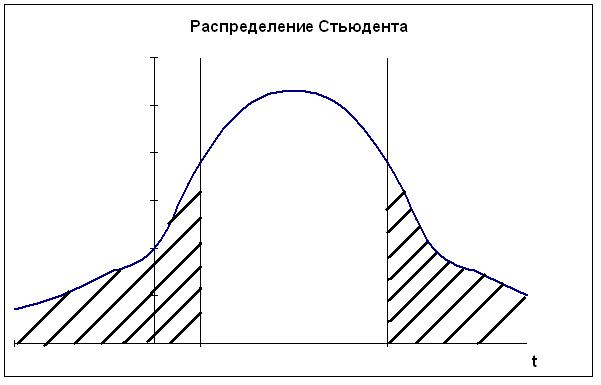 tкрит tкрит Значение t, где область принятия гипотезы пересекается с областью отклонения от гипотезы называется критическим tкрит ( заштрихованная область – область отклонения гипотезы). На основе данных выборки вычисляем tнабл и сравниваем с tкрит. Критические значения затабулированы, рассчитаем их с помощью функции СТЬЮДРАСПОБР(), используя MSExcel. Если |tнабл|> tкрит (α;n-2) данные наблюдений не дают оснований для принятия нулевой гипотезы об отсутствии корреляции в генеральной совокупности с уровнем ошибки α. Принимаем альтернативную гипотезу о том, что корреляция в генеральной совокупности есть, но это не дает оснований для того, чтобы судить о силе. Выборочный коэффициент является существенным, значимым для того, чтобы судить о наличии корреляции в генеральной совокупности. Отличие корреляции от 0 не является случайным. Если |tнабл|< tкрит(α;n-2) данные наблюдений не дают оснований для отклонение нулевой гипотезы. Корреляции в генеральной совокупности нет, это мы можем утверждать с вероятностью α. Коэффициент корреляции статистически незначим, его отличие от 0 случайно. Рассчитаем tнабл для каждого из x. Ho: ρ=0 H1: ρ≠0 Для x1 tнабл = 1,85 tкрит(α=0,05;n-2=34)=2,03 |tнабл|< tкрит коэффициент корреляции r1 статистически не значим, его отклонение от 0 случайно. Для х2 tнабл = 2,16 |tнабл|> tкрит коэффициент корреляции r2 статистически значим, его отклонение от 0 неслучайно. Для х3 tнабл = 1,97 |tнабл|< tкрит коэффициент корреляции r3 статистически не значим, его отклонение от 0 случайно. Регрессионный анализ. Условия Гаусса-МарковаКорреляционный анализ дает возможность определить взаимосвязь двух величин, но не дает ответ на вопрос, на сколько при изменении одного показателя изменяется другой. Для этого существует регрессионный анализ. Регрессионный анализ – метод математической статистики, который изучает регрессионную зависимость генеральной совокупности между некоторыми показателями на основе анализа регрессионной зависимости выборки. На графиках 1, 2, 3 приложения 2 мы видим линию, проходящую через условные средние – линию регрессии. Математическая формула, соответствующая этой линией называется функцией регрессии, которая описывает изменения средних значений y. Условное среднее изменяется по линейному закону, поэтому мы выбираем линейную модель регрессии, которая имеет вид:  С помощью Excel найдем количественную оценку параметров модели. Для этого выделим таблицу и на панели управления выберем Сервис/Анализ данных – регрессия. Либо введем в командной строке в Eviews «ls y c x1 x2 x3 d1 r1 r2 r3». В итоге получим: ŷ= 10199+943*X1+6019,5*X2-604,3*X3+11957,4*d1+15040,7*R1+13532*R2+4232,1*R3  (i=1-7) – коэффициент регрессии, имеет следующий экономический смысл: при изменении независимой переменной на 1, y в среднем изменится на величину при условии, что остальные факторы остаются неизменными. Например,  =943 означает, что при увеличении памяти ноутбука на 1Гб стоимость компьютера увеличивается в среднем на 943 рубля.Так как  <0, зависимость между y и x3 обратная. То есть при увеличении диагонали ноутбука на 1 дюйм стоимость компьютера уменьшится на 604,3 рубля.Следующим этапом регрессионного анализа является оценка качества модели, основанная на теореме Гаусса-Маркова. В данной теореме 1)рассматривается только линейная форма зависимости и 2)независимые переменные могут быть как случайными величинами, так и нет. В теореме Гаусса-Маркова описываются требования к остаткам, от которых зависит качество модели и качество оценок коэффициентов регрессии. Оценки будут хорошими, если будут выполняться следующие условия: а) математическое ожидание (среднее) остатков будет равно нулю; б) между последующими значениями остатков не должно быть корреляции; в) дисперсия остатков должна быть постоянной (гомоскедастичной). В результате, если выполняются эти требования, наши остатки – случайные независимые величины, имеющие нормальное распределение. Проведем проверку каждого коэффициента регрессии. Для этого относительно каждого считается t-статистика по формуле  , которая сравнивается с tкрит(α=0,05;n-k-1=28) (его можно найти в таблице критических точек распределений Стьюдента или в MSExcel через СТЬЮДРАСПОБР(0,05;28)). Принимается гипотеза Н0:  о том, что в генеральной совокупности нет регрессионной зависимости. Н1:  - альтернативная гипотеза. Если |tнабл|> tкрит, то Н0 отклоняется, коэффициент регрессии статистически значим; фактор оказывает существенное влияние, его следует оставить в модели. Если |tнабл|< tкрит, то Н0 принимается, коэффициент регрессии статистически не значим; фактор не оказывает существенное влияние.Но быстрее проверить значимость коэффициентов регрессии через Eviews. Для этого в командную строку вводим «ls y c x1 x2 x3 d1 r1 r2 r3» и в высветившихся данных определяем, что значимо влияет на y только фактор d1. Следовательно, мы неправильно подобрали спецификацию модели. В ходе метода последовательного исключения из модели убираются поочередно факторы с наименьшим незначимым значением t-статистики, пока все коэффициенты регрессии не станут значимыми. 1) Исключаем третий фактор (x3), строим новую модель. Ситуация не меняется. 2) Убираем из модели фактор X1. Коэффициенты обоих оставшихся факторов значимы. Модель выглядит следующим образом: ŷ= 6159,4+5149,9*X2+12223.8*d1+15094,6*R1 + 13561,2*R2 + 4106,7*R3 Анализ качества моделиПроверим качество модели в целом. Принимается гипотеза Н0:  о том, что факторы совместно не влияют на изменение y. Альтернативная гипотеза Н1 подразумевает обратное. Проверка осуществляется на основе критерия Фишера.  . R2 – коэффициент детерминации. Найдем его с помощью программы Eviews в данных по нашей модели.  Или  R2=0,45F набл =  =4,9F табл (  =0,05; n-k-1=30; k=5)=2,5Таким образом, Fнабл>Fтабл . Следовательно, отвергаем Н0, факторы совместно оказывают статистически значимое влияние на y. Модель считается хорошей, когда в ней нет статистически незначимых коэффициентов регрессии и соответственно, по F- критерию она тоже адекватна. То есть нашу последнюю модель можно считать хорошей по этому критерию. Еще одним из этапов анализа качества модели является анализ качества остатков. Остатки – разница между фактическими данными и модельными для каждого периода.  , где ei – остаток в период i. Остатки должны быть случайными, независимыми величинами, распределенными по нормальному закону. Только если эти требования выполняются, можно переходить к другим методам проверки качества модели. Существует графический и аналитический способ анализа остатков. Графический способ подразумевает построение графика остатков. Eviews автоматически показывает график остатков, когда мы считаем теоретический y и остатки. На графике остатков приложения 3 видно, что выбросов нет, т.е. нет остатков, которые в 4-6 раз больше других. Следовательно, в первоначальных данных нет нетипичных наблюдений, дисперсия остатков постоянна. Такие остатки называются гомоскедастичными. Поскольку математическое ожидание остатков равно 0, можно сделать вывод о том, что остатки распределены по нормальному закону. Одним из аналитических методов является проверка на наличие автокорреляции в остатках. Автокорреляция – это корреляция между уровнями ряда и его последующими значениями. Наличие автокорреляции может свидетельствовать о том, что в остатках отражается какой-либо фактор, значительно влияющий на результирующий признак, однако не включенный в модель. Проверка на наличие автокорреляции осуществляется на основе критерия Дарбина-Уотсона. Но поскольку у нас не временной ряд, мы не можем применять этот метод. Также наличие гетероскедастичности модели регрессии можно проверить с помощью теста Голдфелда-Куандта и теста Уайта. Тест Голдфелда-Куандта (Goldfeld-Quandt) Тест Голдфелда-Куандта проводится следующим образом: 1 шаг. Упорядочиваем все наблюдения в соответствии с увеличением значений переменной x2 2 шаг. Весь ряд наблюдений делим на 3 части, при этом в первой и третьей части находится одинаковое число наблюдений. 3 шаг. Для первой и третьей части строим регрессию и определяем RSSI и RSSIII. RSSI=  RSSIII= 4 шаг. Принимаем гипотезу о том, что у нас дисперсия (разброс остатков) не зависит от значения x2. Ho: δ  =δ , i≠j (дисперсия постоянна, гомоскедастичность)H1: δ ≠δ, i≠j (дисперсия непостоянна, гетероскедастичность)Разброс измеряется дисперсией. По условиям Гаусса-Маркова дисперсия остатков должна быть постоянной (не зависящей от номера x). Гипотеза проверяется с помощью критерия Фишера:  Fнабл= Fтабл(α=0,05; k-m-1;k-m-1), где k-m-1 – число степеней свободы, k - число наблюдений в первой и третьей части, m - число переменных (факторов), 1 – из-за наличия константы. Нарисуем графики распределения Фишера. 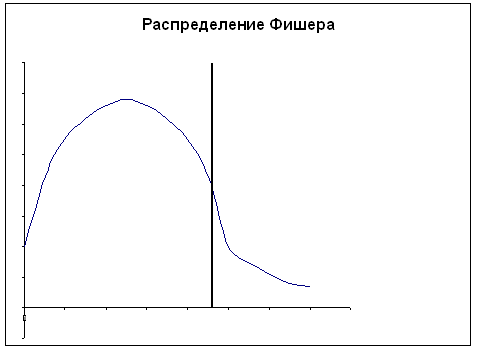 Fтабл Если Fнабл≥Fтабл принимается гипотеза Н1 о наличии гетероскедастичности. Если Fнабл≤Fтабл, принимается гипотеза Н0 о постоянстве дисперсии, гомоскедастичности. Тест Уайта (White) Используя Eviews, можно провести проверку качества модели регрессии с помощью теста Уайта. Идея этого теста заключается в том, что если в остатках есть гетероскедастичность, то в остатках остались какие-то нелинейные зависимости от исследованных факторов. Целью данного теста является проверка наличия в остатках нелинейной зависимости от факторов. Шаг 1. Строим модель регрессии ŷ=  +  *X2+  *d1+  *R1 +  *R2 +  *R3. Находим остатки для регрессии.Шаг 2. Строится модель квадрата остатков от факторов, квадратов факторов и пересечений факторов (фиктивные переменные не рассматриваем)  Шаг 3. Если остатки гетероскедастичны, то квадраты факторов влияют на остатки, то есть коэффициенты регрессии ai статистически значимы, и мы можем проверить совместное влияние всех факторов на квадраты остатков с помощью критерия Фишера. Принимаем гипотезу о том, что все факторы совместно не влияют на квадраты остатков. Н0: ai =ak=0 Альтернативная гипотеза H1 утверждает, что это не так.  В критерии Уайта nR2 сравнивается с χ2(N-1), где n – число наблюдений, N – число факторов. Для расчетов воспользуемся Eviews. Так как probability=0,157911 и больше уровня значимости α=0,05, следовательно, в данной модели регрессии гетероскедастичность отсутствует и дисперсия является постоянной. Тест Чоу 1) У нас есть модель регрессии для 36 наблюдений: ŷ= 6159,4+5149,9*X2+12223,8*d1+15094,6*R1 + 13561,2*R2 + 4106,7*R3 Ошибка  48187566512) Выделим 2 группы. Первая – с весом ноутбука до 2,5 кг (x2<2,5), а вторая – с весом ноутбука больше или равно 2,5 кг (x2≥2,5). С помощью Eviews для первой группы строим модель: ŷ= 9823,8+3379,9*X2+14466,8*d1+15548,3*R1 + 17975,6*R2 + 4296,4*R3 Ошибка  17307427503) Модель регрессии для второй группы: ŷ= -23270,2+15266,4*X2+11503,9*d1+13020,6*R1 + 6207,6*R2 - 3823,7*R3 Ошибка  19896527844) Принимаем гипотезу H0 о том, что не произошло никаких изменений в этих двух группах (при =0,05)Н0:  , i=0…kH1:  5) Проверяем гипотезу с помощью критерия Фишера  Fнабл=1,18 Fтабл( =0,05; n-2*(k+1)=24;k+1=6)=2,5Таким образом, Fнабл Фиктивные переменныеФиктивные переменные применяются для отражения качественных признаков. Причем качественные признаки принимают 2 значения, поэтому они еще называются бинарными переменными. Мы ввели фиктивную переменную d1, равную 1 при наличии процессора Core 2 Duo и нулю при его отсутствии. Может быть несколько однородных качественных переменных. Например, определенная модель ноутбука. Главное – это чтобы число однородных качественных переменных было на единицу меньше, чем число рассматриваемых признаков. Мы рассматриваем 4 бренда производителей компьютеров, поэтому вводим 3 фиктивные переменных R1, R2 и R3. R1 равен 1 у компьютеров марки HP, R2 – Toshiba и R3 – Acer. Если модель – Asus, то R1=R2=R3=0. Определим, значимо ли бренд производителя влияет на стоимость ноутбука. В модели регрессии без учета бренда 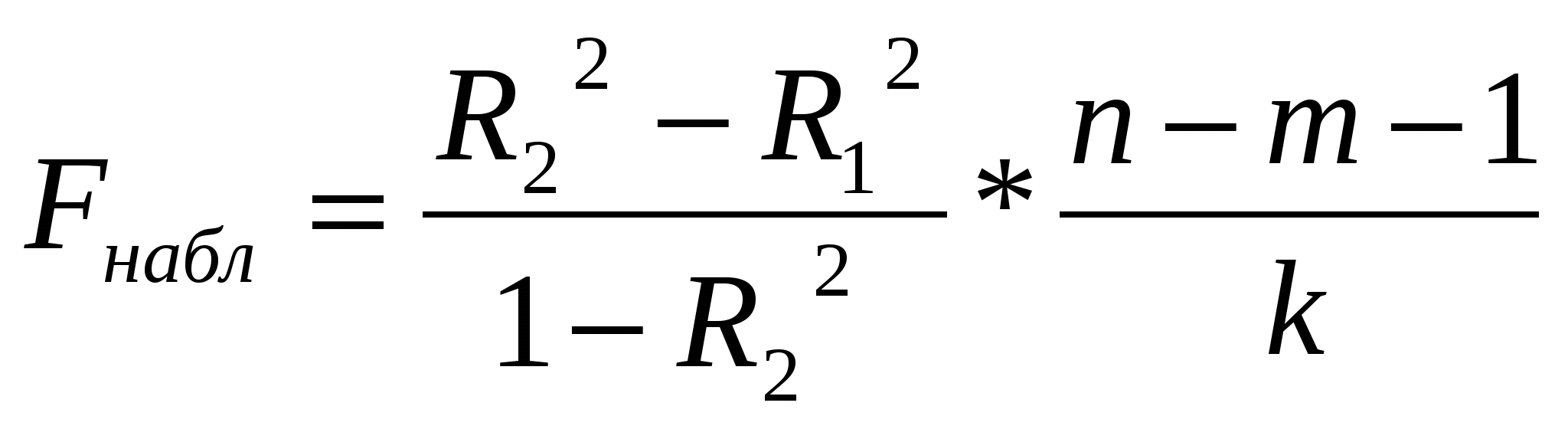 (данные получены из Eviews), в модели регрессии с учетом бренда  . Принимаем гипотезу Н0:  о том, что бренд производителя не влияет на стоимость ноутбука. Альтернативная гипотеза Н1 подразумевает, что это не так. Гипотеза проверяется с помощью критерия Фишера (уровень значимости равен 0,05). , где n – число наблюдений, m – число качеств, которые мы учитываем в большей модели, k – число исключенных из большей модели качеств.  Таким образом,  >  . Гипотеза Н0 отвергается, бренд производителя значимо влияет на стоимость ноутбука.Теперь проверим, значимо ли наличие процессора Core 2 Duo (фиктивная переменная d1) влияет на стоимость компьютера. Соответственно, используем те же самые формулы. В модели регрессии без учета наличия данного процессора  (данные получены из Eviews), в модели регрессии с учетом наличия . Принимаем гипотезу Н0:  о том, что наличие или нет процессора Core 2 Duo не влияет на стоимость ноутбука. Альтернативная гипотеза Н1 подразумевает, что это не так. Гипотеза проверяется с помощью критерия Фишера (уровень значимости равен 0,05).  Таким образом, > . Гипотеза Н0 отвергается, наличие процессора Core 2 Duo значимо влияет на стоимость ноутбука.ЗаключениеВ данной работе мы исследовали зависимость цены на ноутбуки на российском рынке от ряда показателей: диагонали, веса, объема памяти RAM, наличия процессора Core 2 Duo, а также бренда. Данный анализ и все расчеты проводились с использованием таких компьютерных программ, как MSExcel и Eviews. Изначально, была предложена следующая спецификация модели: То есть, это линейная модель регрессии, учитывающая 7 факторов, из них 4 фиктивные переменные. Но в ходе проверки статистической значимости каждого полученного коэффициента регрессии выяснилось, что отклонение коэффициентов  и  от 0 является случайным, то есть диагональ и объем памяти RAM не оказывают существенного влияния на цену ноутбука, в результате чего они были исключены из нашей модели. Также после исключения 2 факторов было проверено качество новой модели (наличие автокорреляции остатков и гетероскедастичности). Данный анализ был проведен несколькими тестами (Голдфелда-Куандта, Уайта и Чоу), и в результате было получено, что в данной модели отсутствует автокорреляция и гетероскедастичность. Следовательно, наша модель является хорошей. В итоге была получена линейная модель регрессии, учитывающая 5 факторов, в том числе 4 фиктивных переменных, и имеющая следующий вид: ŷ= 6159,4+5149,9*X2+12223.8*d1+15094,6*R1 + 13561,2*R2 + 4106,7*R3 То есть, цена на ноутбуки прямо пропорциональна его весу, а также зависит от наличия процессора Core 2 Duo и бренда. ПриложенияПриложение 11
Приложение 2 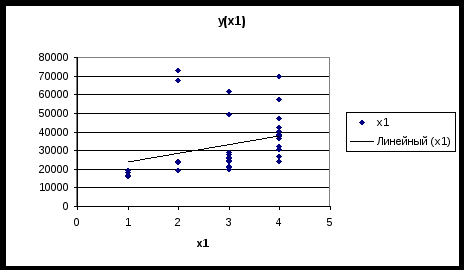 График 1 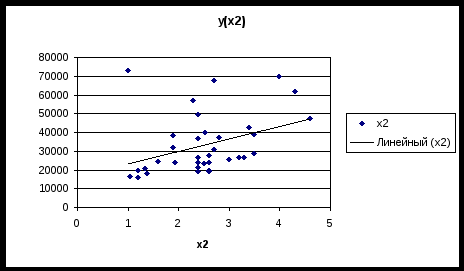 График 2 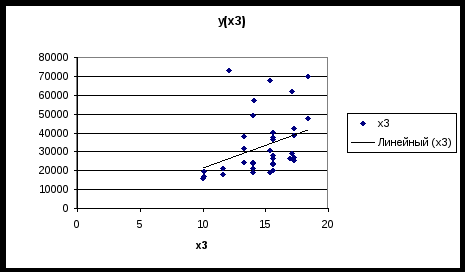 График 3 Приложение 3 График остатков (Eviews) 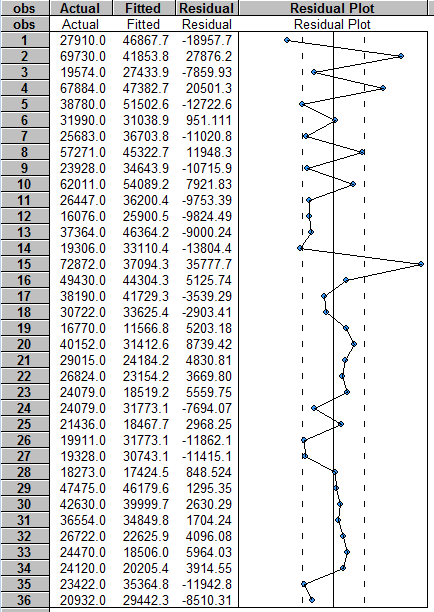 Приложение 3 (продолжение) Графики остатков (Excel) 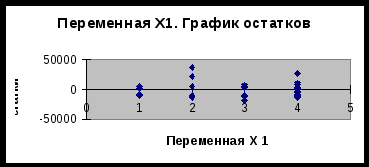 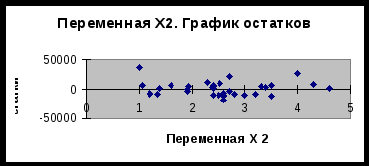 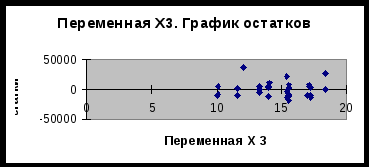 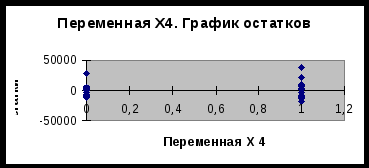 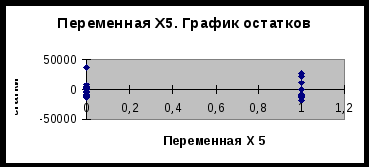 1 Таблица составлена авторами на основании данных сайта «notebook.tkat.ru» по состоянию на 13.12.09. |