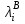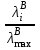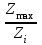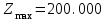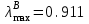Курсовик. ГОТОВЫЙ)))))))))))))))))))))))))))))). Анализ технического задания
 Скачать 1.8 Mb. Скачать 1.8 Mb.
|
1 2 Сочетания №1,2 является наиболее критичными, в них входят все предпосылки.  +   + +         Q3 Q2 Q1 Q4 Q5 Q6 Q10  Q11 Q(x) Q12         Q1 Q2 Q3 Q4 Q10 Q11 Q12 Q7 Q8  Q9 Q1 Q2 Рис.Эквивалентное дерево происшествий МОС  Посчитанная вероятность МПС совпадает с исходной вероятностью 0.160  3 Модельный эксперимент 3 Модельный эксперимент 3.1 Построение имитационной и динамической моделей Рассматриваемая модель дерева аварии является статистической и позволяет оценить априорную вероятность возникновения аварии без учета динамики (времени) и законов распределения случайных величин характеризующих предпосылки. Для оценки динамики изменения вероятности аварии во времени, а также учета законов распределения случайных величин применяется динамическая модель дерева аварии. Эта модель является имитационной и позволяет оценить динамические характеристики процессов аварийности и травматизма в техносфере: Эксперимент   Т Т Q(X) W(X) TВ Характеристики: относительная частота появления событий; среднее время выполнения тех.процесса без происшествий (наработка на отказ). Точность и достоверность оценки этих характеристик зависит от модельного времени (интервала наблюдений). Чем больше модельное время, тем точнее результат. В комплексной модели значения модельного времени измеряются в шагах и могут соответствовать любым единицам времени в зависимости от задачи, чем меньше априорная вероятность Q(X),тем больше должно быть значение модельного времени. Техника имитационного моделирования предусматривает многократное повторение эксперимента. В модели дерева происшествий исходные предпосылки (6,7,8,9,10), заданные константами, заменяем блоками генераторов случайных чисел с заданным законом распределения. а) unifrnd (a,b) – равномерное распределение случайных чисел в интервале от a и b. б) normrnd (m,s) – нормальное распределение с параметрами m – мат. ожидание и s – дисперсия случайно величины. в) exprnd (L) – показательное распределение с параметром L – интенсивность. 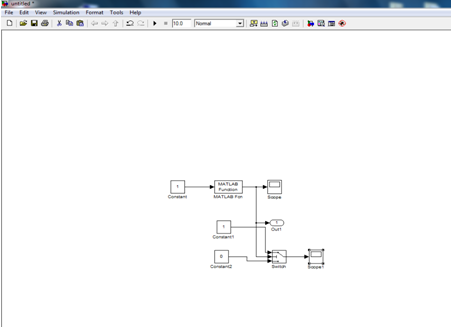 Рис.3.1 Генератор случайных  чисел чисел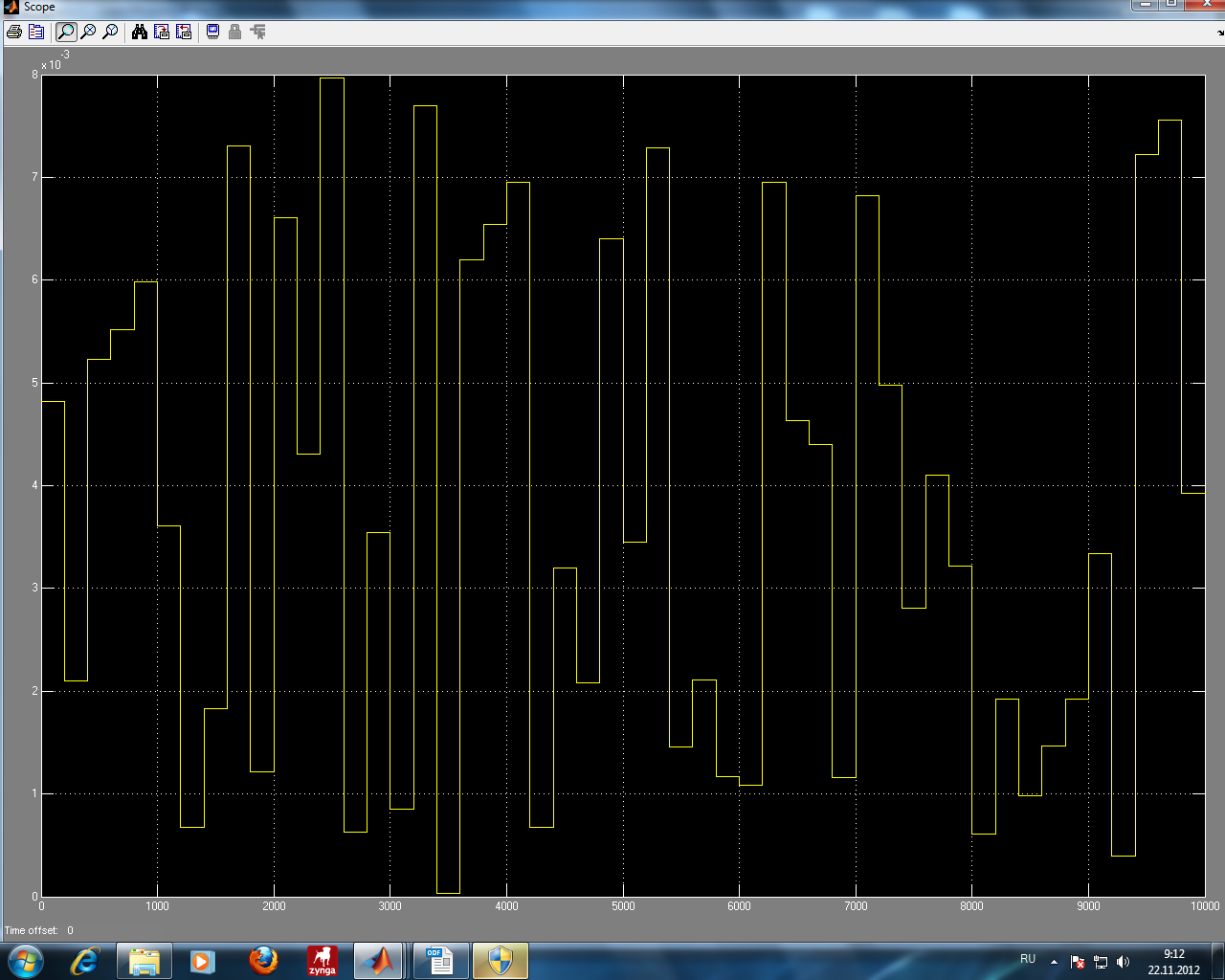 Рис.3.2 График изменения предпосылки Р1(закон равноерный)   Рис.3.3 График изменеия предпосылки Р2(закон равномерный)  Рис.3.4 График изменения предпосылки Р3(закон экспоненциальный)  Рис.3.5 График изменения предпосылки Р4(закон раномерный)  Рис.3.6 График изменения предпосылки Р10(закон экспоненциальный)  Р Р ис.3.7 График изменения предпосылки Р11(закон экспоненциальный) 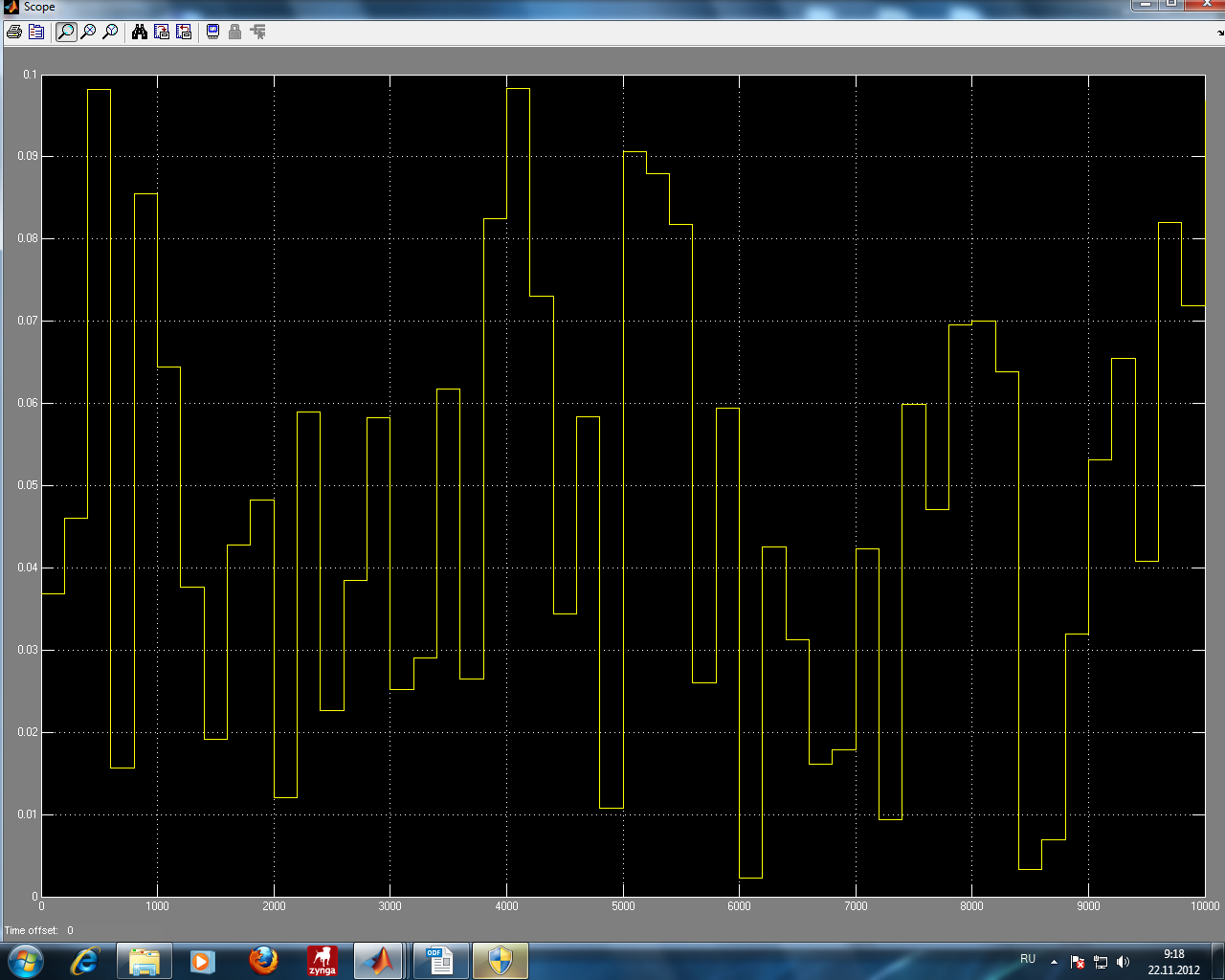 Рис.3.8 График изменения предпосылки Р12(закон равномерный) 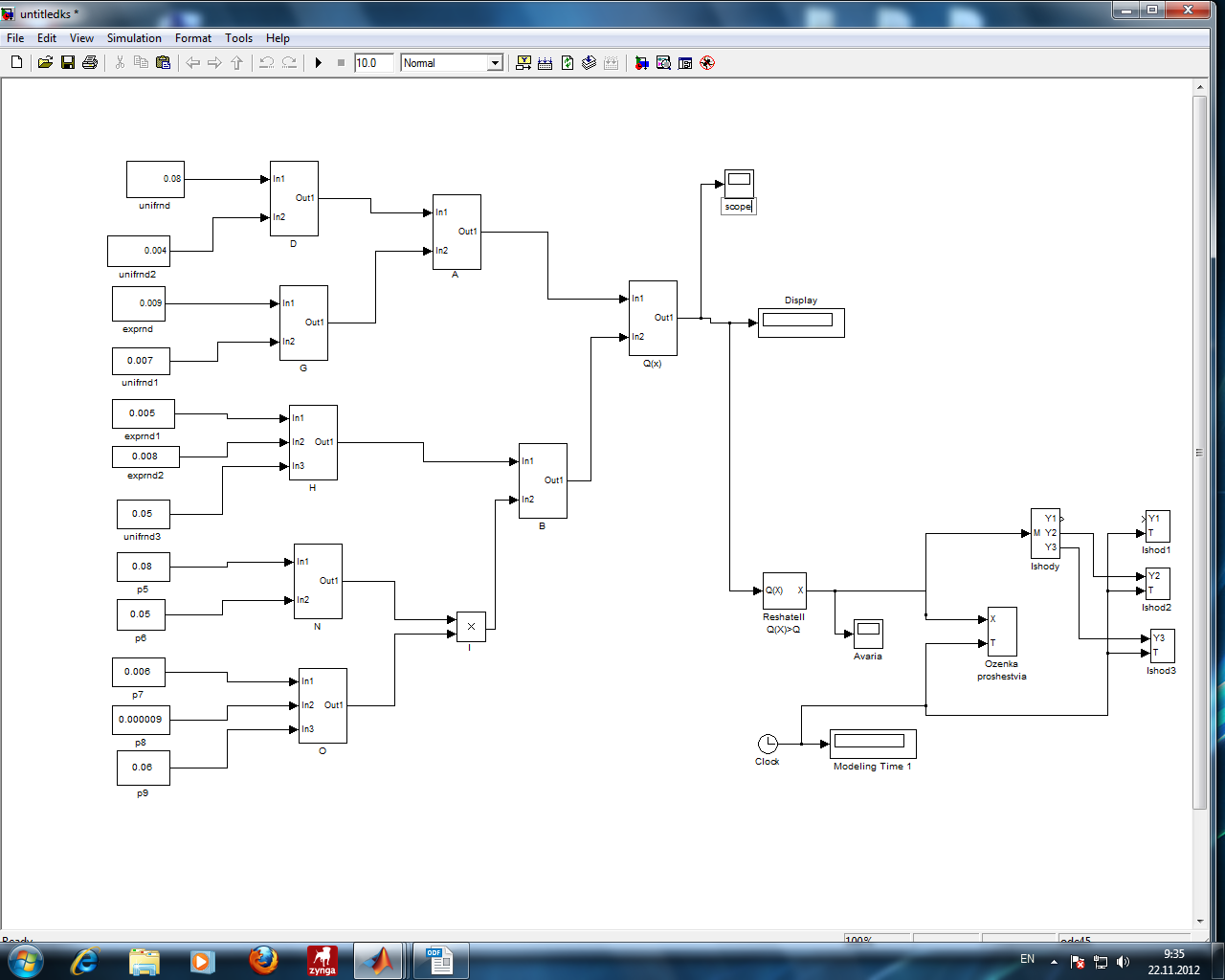 Рис.3.9 Динамическая модель дерева происшествий 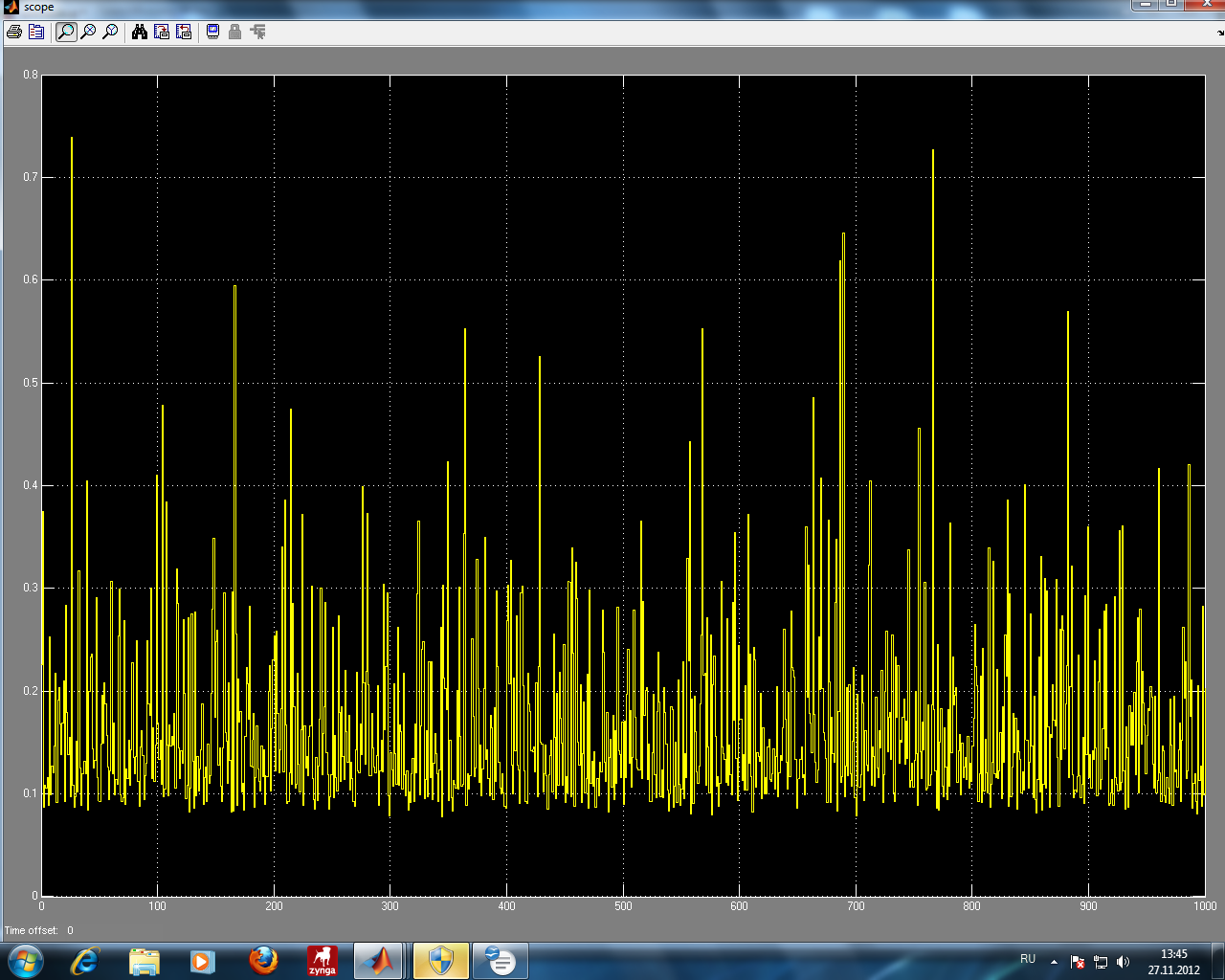 Рис.3.10 График изменения вероятности Q(x) 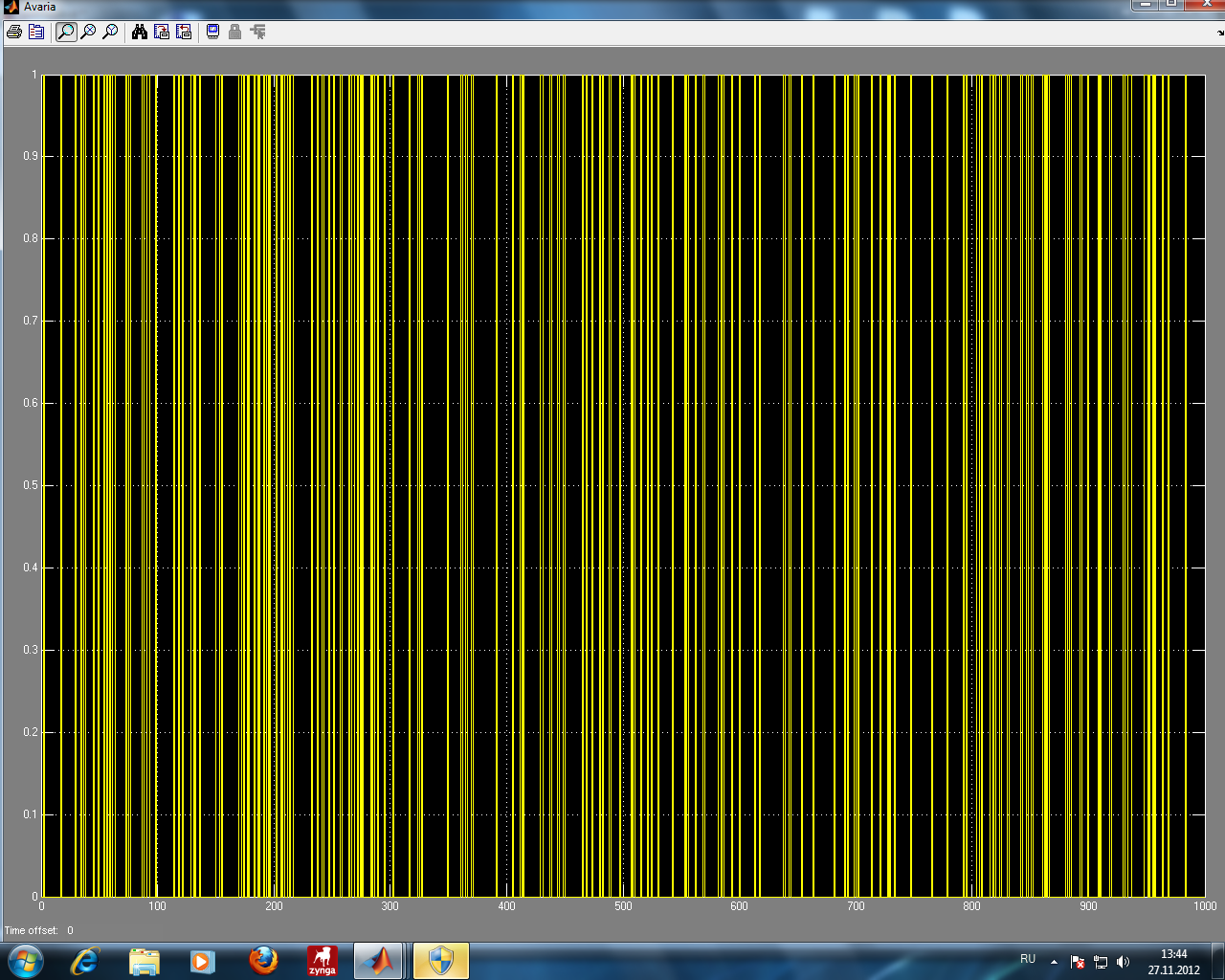 Рис.3.11 График аварийности
 В ходе статистического эксперимента была многократно запущена модель и получено среднее значение вероятность Q(x) из 10 результатов, которая практически совпадает и ранее посчитанной вероятность Q(x)=0,160  3.2 Оптимизация показателей безопасности 3.2 Оптимизация показателей безопасностиПри анализе результатов моделирования оценка параметров безопасности дается с учетом смысла модельного времени Т равного 1000 часам. Таблица 3.2 Мероприятия по снижению вероятностей предпосылок
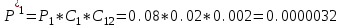 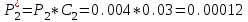 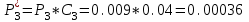 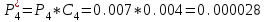 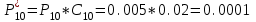 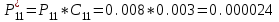 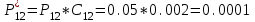 После проведения мероприятий по снижению риска возникновения происшествий были пересчитаны значения вероятностей значимых и критичных предпосылок. Новые значения занесены в модель дерева происшествий и получена новая вероятность 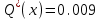 исходя из того, что исходя из того, что 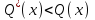 . .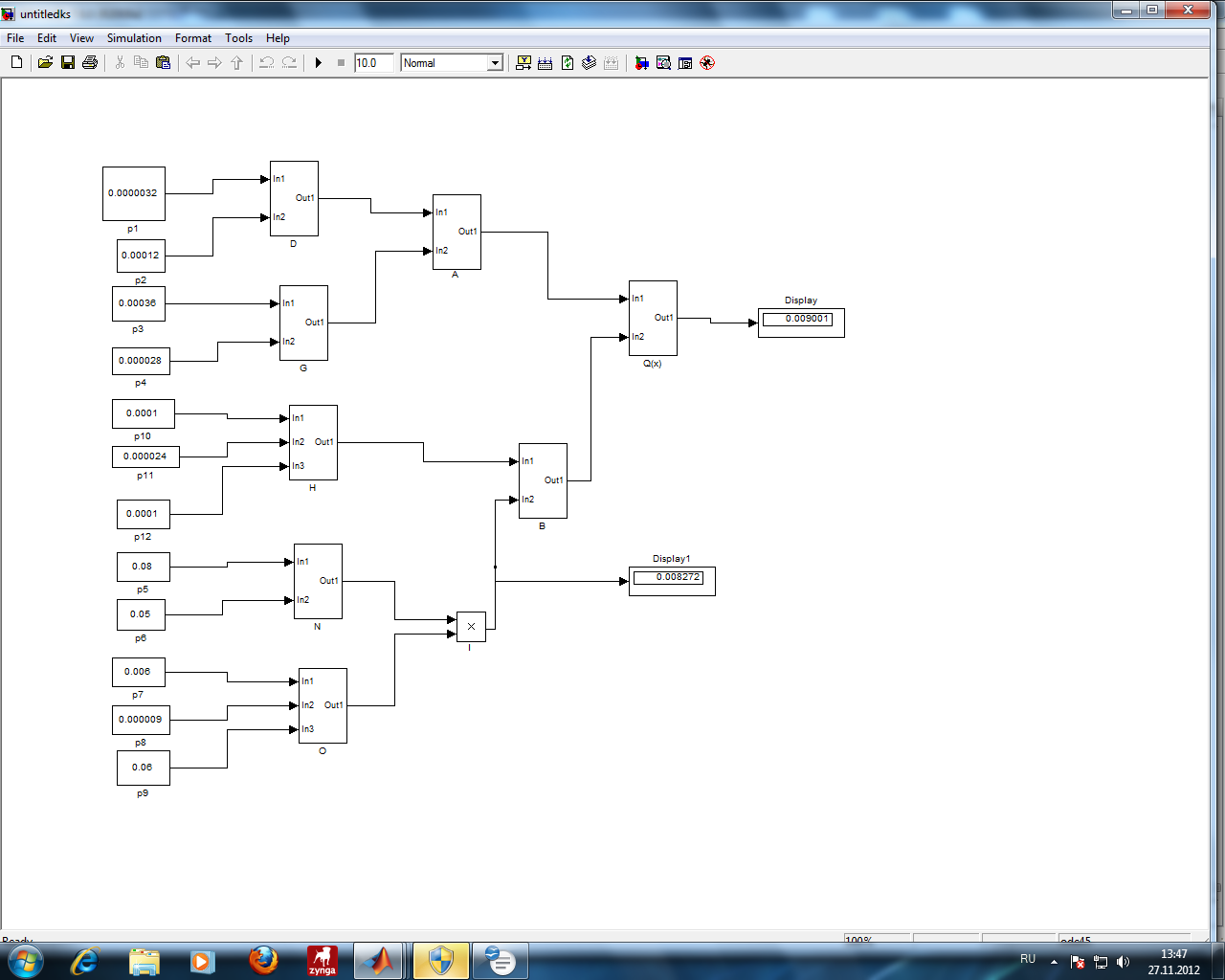  Рис.3.12 Модель дерева происшествий с мероприятиями по снижению риска возникновения происшествия 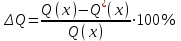 , (3.1) , (3.1)где 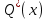 - вероятность Q(x) после оптимизации. - вероятность Q(x) после оптимизации.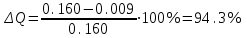 . .Вследствие проведения мероприятий вероятность возникновения происшествий Q(x) уменьшилась на 94.3 %. Оценка снижения техногенного риска: 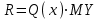 , (3.2) , (3.2)где R - риск, MY – средний ущерб. 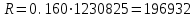 руб. руб.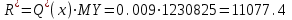 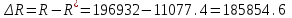 руб. руб.Проведение мероприятий по оптимизации сопровождается затратами на них. 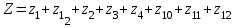 , (3.3) , (3.3)где Z – затраты. 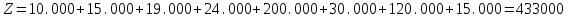 руб. руб.Эффективность проведения мероприятий: 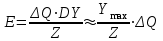 , (3.4) , (3.4)где DY – дисперсия затрат, Ymax – максимальный ущерб. 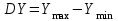 , (3.5) , (3.5)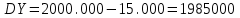 руб., руб., 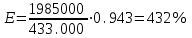 Эффективность проведенных мер составляет 432%. Таблица 3.3 Выбор альтернативного решения
Проанализировав импакт-фактор и затраты для каждого мероприятия, возьмем Р1, Р12, Р2,Р12 так как значения Vi у них самые большие, а затраты самые наименьшие Z1=10.000, Z1.2=15.000, Z12=15.000. Заносим в модель дерева происшествий значения вероятностей (P1=0.08, P2=0.004, P12=0.05) только этих мероприятий. 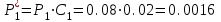 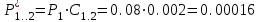 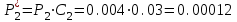 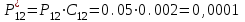  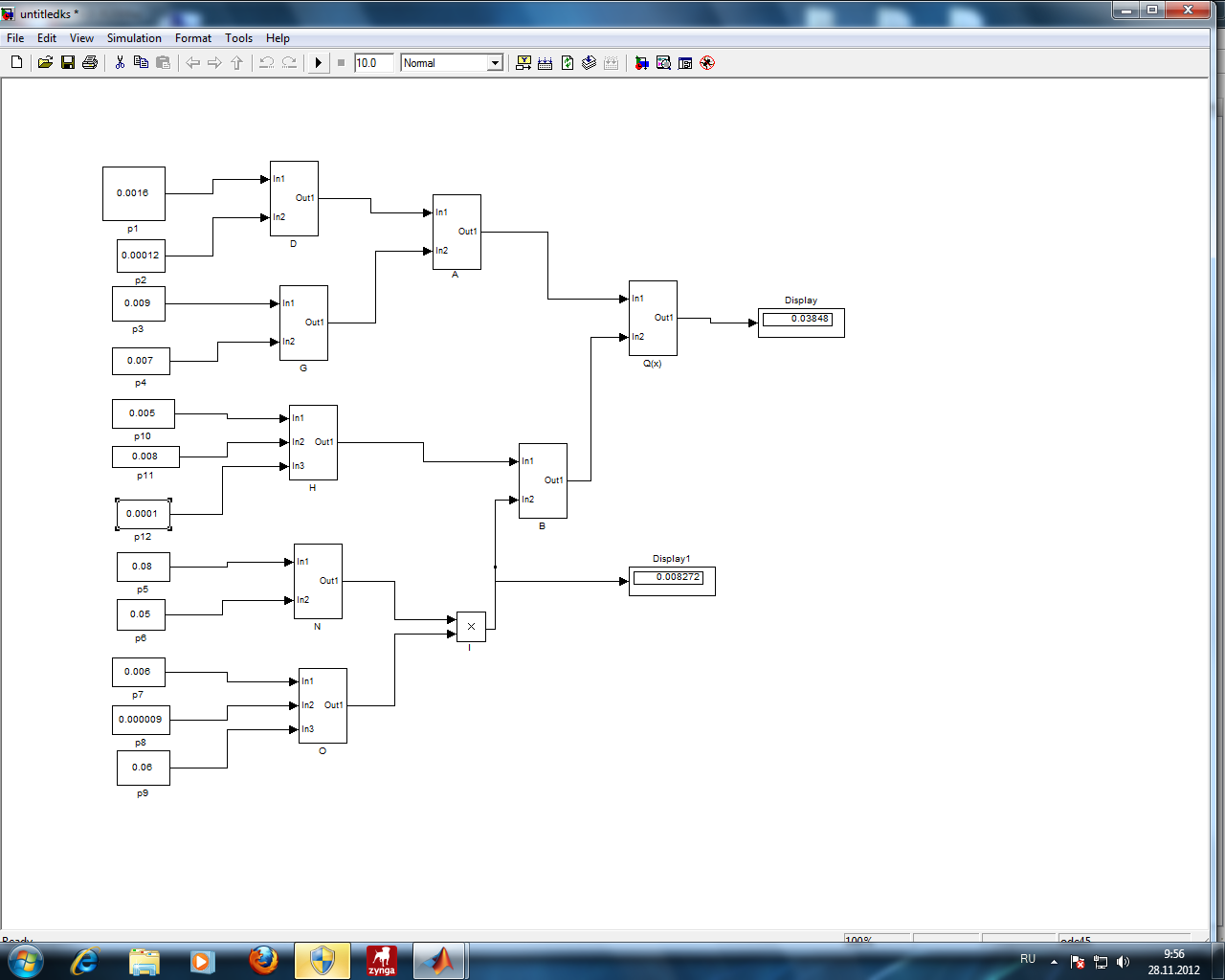  Рис.3.13 Модель дерева происшествий с альтернативными решениями Q*=0.03<0.160 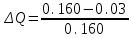 =0.81% =0.81% Эффективность проведения альтернативных мероприятий: 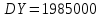 руб., руб.,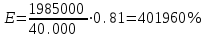 Значение эффективности увеличилось и составило 401960%.  Заключение ЗаключениеВ ходе проведения данной курсовой работы было рассчитано Q(x)=0,160 и построена зависимость головного события при которых изменяли исходные вероятности предпосылок (0,1). Выявили критичные Р5,Р6 и значимые предпосылки Р1,Р2,Р3Р4,Р10,Р11,Р12 . С помощью MatLab построили модели происшествия . После построения результат вероятности головного события сходится с посчитанным ранее результатом . Провели модельный эксперимент и получили данные : N=161.6 ;W=0.1616;Тб=6.17;  Список литературы Список литературы1.Белов С.В., Ильницкая А.В., Козьяков А.Ф., Морозова Л.Л., Павлихин Г.П., Переездчиков И.В., Сивков В.П., Якубович Д.М. Безопасность жизнедеятельности: Учебник для вузов / Под ред. С.В. Белова. - М.: Высш. шк., 1999. - 553 с 2.Вознесенский В.В., Зайцев А.П. Новейшие средства защиты органов дыхания и кожи. - М.: Военные знания, 2000. – 87 с. 3. Жилов Ю.Д., Куценко Г.И., Назарова Е.Н. Основы медико-биологических знаний. – М.: Высшая школа, 2001. – 321с. 4. Леонтьева И.Н., Гетия А.Л. Безопасность жизнедеятельности.- М.: 2008.-92с. Приложение А . 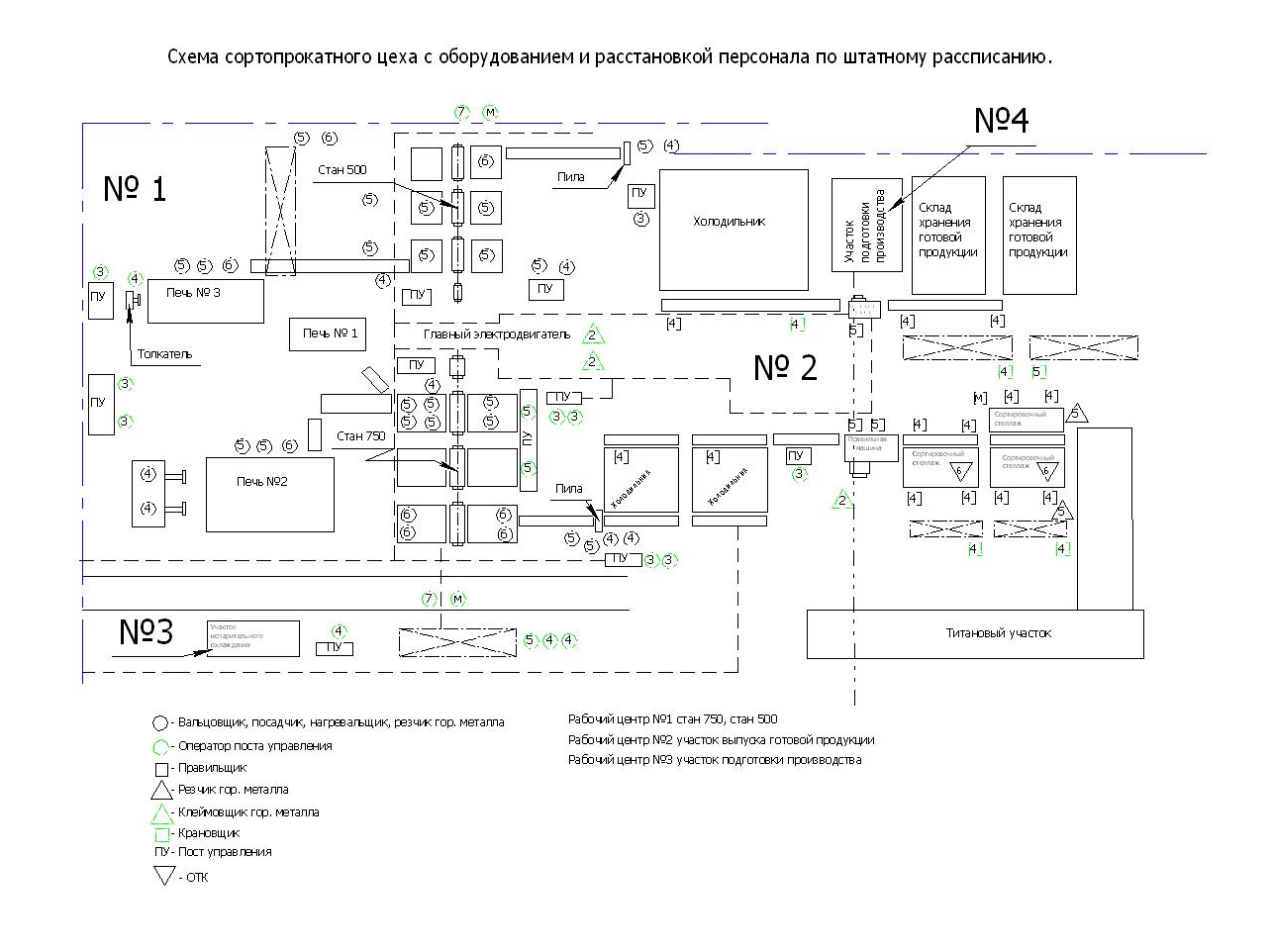 Приложение В Таблица №1. Температурные режимы нагрева время выдержки под прокатку, температура окончания деформации и условия охлаждения.
Приложение С Таблица №2. Нормы обрези от резки головной и донной частей слитков.
Приложение D 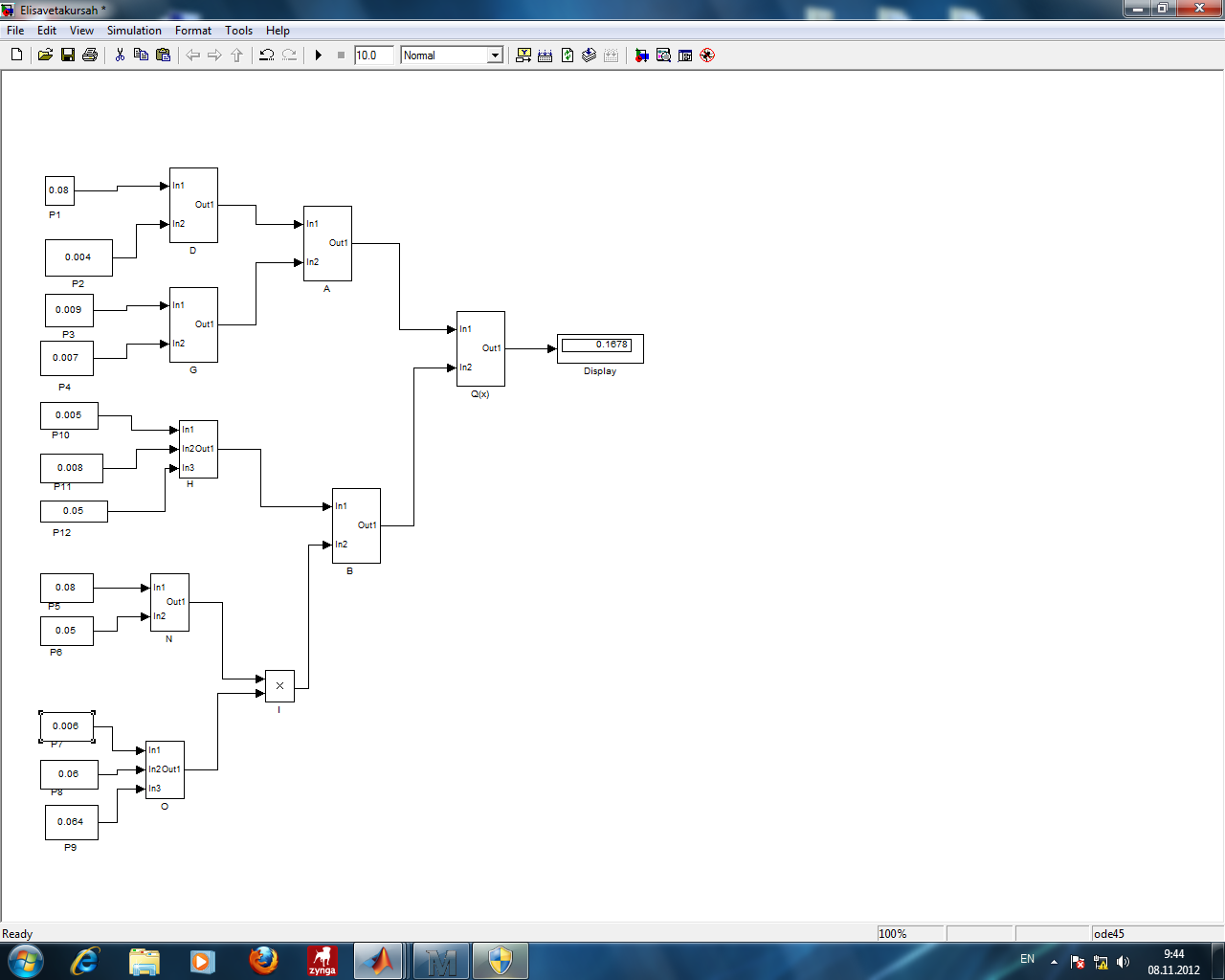 1 2 |