Математика. Задачи готовые. Задача 8 Условие задачи

• Название: Задача 8 Условие задачи
• Анкор: Математика
• Дата: 20.12.2022
• Размер: 191.5 Kb.
• Имя файла: Задачи готовые.doc
• Тип: Задача; #854297

ЗАДАНИЕ №1

Задача №8

Условие задачи:

Из 20 отобранных деталей 5 изготовлено на станке №1, 10 изготовлено на станке №2, остальные — на станке №3. Вероятность изготовления стандартной детали на станке №1 равна 0,96, на станке №2 — 0,98. Найти вероятность изготовления стандартной детали на станке №3, если вероятность при случайном отборе получить стандартную деталь из вышеуказанных 20 равна 0,98.

Решение задачи:

Из случайно отобранных 20 деталей, детали изготовленные на станках относятся как 5:10:5, т. е. 1:2:1.

Вероятность стандартных деталей на первом — 0.96

На втором — 0.98

На третьем — X

Вероятность стандартных деталей из этих 20 — 0.98

По формуле полной вероятности:









ЗАДАНИЕ №2

Задача №8

Условие задачи:

Из числа авиалиний некоторого аэропорта 60% - местные, 30% - по СНГ и 10% - в дальнее зарубежье. Среди пассажиров местных авиалиний 50% путешествуют по делам, связанным с бизнесом, на линиях СНГ таких пассажиров - 60%, на международных - 90%. Из прибывших в аэропорт пассажиров случайно выбирается один. Чему равна вероятность того, что он:

а) бизнесмен

б) прибыл из стран СНГ по делам бизнеса

в) прилетел местным рейсом по делам бизнеса

г) прибывший международным рейсом бизнесмен

Р ешение задачи:

А) p = 0,6·0,5 + 0,3·0,6 + 0,1·0,9 = 0,3 + 0,18 + 0,09 = 0,57 или 57%

б) p = 0,3·0,6 = 0,18 или 18%

в) p = 0,6·0,5 = 0,3 или 30%

г) p = 0,1·0,9 = 0,09 или 9%
ЗАДАНИЕ №3

Задача №8

Условие задачи:

В лотерее разыгрывается 100 баллов. Выигрыши выпали на 20 билетов. Некто приобрел 5 билетов. Найти вероятность следующих событий: а) выигрыш выпадет на все 5 билетов. Б) выигрыш выпадет хотя бы на 1 билет. В) выигрыш выпадет на 2 билета

Решение задачи:

Если обозначить С(m,n) - число сочетаний n из m, то есть

С(m,n) = m!/(n!*(m-n)!)

то общее число ВАРИАНТОВ вынуть 5 билетов из 100 равно C(100,5)

При этом, если известно, что в этих 5 билетах ровно к выгрышных и (5 - к) невыгрышных, то число разных вариантов сильно сокращается, и равно числу вариантов вынуть к из 20, умножить на число вариантов выбрать 5 - к из 80 (а почему умножить? на каждый вариант из C(20, к) сочетаний первой группы приходится С(80, 5 - к) второй..)

Поэтому вероятность попасть в благоприятный исход равна

С(20, к)*С(80, 5 - к)/C(100, 5);

1. в первом случае к = 5, 5 - к = 0, то есть

р = С(20,5)/С(100,5)

2. событие дополнительно событию, когда достали 5 невыгрышных билетов, то есть

р = 1 - С(80,5)/С(100,5)

3. р = С(20, 2)*С(80, 3)/C(100, 5);

ЗАДАНИЕ №4

Задача №8

ЗАДАНИЕ №6

Задача №8

На трех железнодорожных станциях А₁, А₂ и А₃ скопилось 120, 110 и 130 незагруженных вагонов. Эти вагоны необходимо перегнать на железнодорожные станции В₁, В₂, В₃, В₄ и В₅. На каждой из этих станций потребность в вагонах соответственно равна 80, 60, 70, 100 и 50. Тарифы перегонки одного вагона определяются матрицей:

Р 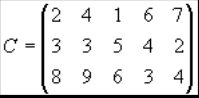ешение задачи:

Составьте такой план перегонок вагонов, чтобы общая стоимость была минимальной.

Решение

Занесем исходные данные в распределительную таблицу.

	B1	B2	B3	B4	B5	Запасы
A1	2	4	1	6	7	120
A2	3	3	5	4	2	110
A3	8	9	6	3	4	130
Потребности	80	60	70	100	50

Проверим закрытость системы.

∑А=120+110+130=360

∑В=80+60+70+100+50=360

Условие баланса соблюдается. Запасы равны потребностям.

1. 
   Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.
   

	B1	B2	B3	B4	B5	Запасы
A1	2[50]	4	1[70]	6	7	120
A2	3[30]	3[30]	5	4	2[50]	110
A3	8	9[30]	6	3[100]	4	130
Потребности	80	60	70	100	50

В результате получен первый опорный план, который является допустимым, т.к. все вагоны вывезены на станции, которым они нужны, потребность станций в вагонах удовлетворена, а план соответствует системе ограничений транспортной задачи.

1. 
   Подсчитаем число занятых клеток, их 7, а должно быть m+n-1=7. Следовательно, опорный план является невырожденным.
   
2. 
   Проверим оптимальность опорного плана. Найдем потенциалы u_i, v_i по занятым клеткам таблицы, в которых u_i+v_i=c_ij, полагая, что u_i=0.
   

u₁+v₁=2; 0+v₁=2; v₁=2.

u₁+v₃=1; 0+v₃=1; v₃=1.

u₂+v₁=3; u₂+2=3; u₂=1.

u₂+v₂=3; 1+v₂=3; v₂=2.

u₃+v₂=9; u₃+2=9; u₃=7.

u₃+v₄=3; 7+v₄=3; v₄=-4.

u₂+v₅=2; 1+v₅=2; v₅=1.

	v1=2	v2=2	v3=1	v4=-4	v5=1
u1=0	2[50]	4	1[70]	6	7
u2=1	3[30]	3[30]	5	4	2[50]
u3=7	8	9[30]	6	3[100]	4

Опорный план не является оптимальным, т.к. существуют оценки свободных клеток, для которых u_i+v_i>c_ij:

(3;1): 7+2>8; ∆31=7+2-8=1.

(3;3): 7+1>6; ∆33=7+1-6=2.

(3;5): 7+1>4; ∆35=7+1-4=4.

Выбираем максимальную оценку свободной клетки (3;5): 4.

Для этого в перспективную клетку (3;5) ставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-». Цикл приведен в таблице.

	v1=2	v2=2	v3=1	v4=-4	v5=1
u1=0	2[50]	4	1[70]	6	7
u2=1	3[30]	3[30][+]	5	4	2[50][-]
u3=7	8	9[30][-]	6	3[100]	4[+]

Из грузов x_ij стоящих в минусовых клетках, выбираем наименьшее, т.е. min(30,50)=30. Прибавляем 30 к объемам грузов, стоящих в плюсовых клетках и вычитаем 30 из объемов грузов стоящих в минусовых клетках. В результате мы получим новый опорный план.

	B1	B2	B3	B4	B5	Запасы
A1	2[50]	4	1[70]	6	7	120
A2	3[30]	3[60]	5	4	2[20]	110
A3	8	9	6	3[100]	4[30]	130
Потребности	80	60	70	100	50

Проверим оптимальность опорного плана. Найдем потенциалы u_i, v_i по занятым клеткам таблицы, в которых u_i+v_i=c_ij, полагая, что u_i=0.
u₁+v₁=2; 0+v₁=2; v₁=2

u₁+v₃=1; 0+v₃=1; v₃=1

u₂+v₁=3; u₂+2=3; u₂=1

u₂+v₂=3; 1+v₂=3; v₂=2

u₂+v₅=2; 1+v₅=2; v₅=1

u₃+v₅=4; u₃+1=4; u₃=3

u₃+v₄=3; 3+v₄=3; v₄=-0

	v1=2	v2=2	v3=1	v4=0	v5=1
u1=0	2[50]	4	1[70]	6	7
u2=1	3[30]	3[60]	5	4	2[20]
u3=3	8	9	6	3[100]	4[30]

Опорный план является оптимальным, т.к. для всех ui+vi≤cij.

Затраты составят: F(x)=2*50+1*70+3*30+3*60+2*20+3*100+4*30=900.