Множественная регрессия. лабораторная работа множ. регр. Анализ в ms excel 2 вариант Голосова Дарья бин31оз Результативный признак Y2 фактическая стоимость введенной в отчетном год
 Скачать 94.14 Kb. Скачать 94.14 Kb.
|
|
МНОЖЕСТВЕННЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ В MS EXCEL 2 вариант Выполнила: Голосова Дарья БИН-31оз Результативный признак: Y2 - фактическая стоимость введенной в отчетном году жилой площади для застройщика, тыс. руб.; Факторные признаки: Y1 - ввод общей площади жилых домов, кв.м.; Y3 - общая стоимость реализуемых инвестиционных проектов, тыс. руб.; Y4 - стоимость работ, выполненных с начала реализации инветиционных проектов, тыс. руб.; X5 - ввод квартир, ед.; Х6 - общая площадь жилых домов в незавершенном строительстве, кв. м.; Исследуем на основе множественной регрессионной модели зависимость результативного признака от рассматриваемых факторных признаков. Исходные данные:
Проверка исходных данных на мультиколлинеарность Прежде чем переходить к построению регрессионной модели, необходимо проверить объясняющие переменные на наличие мультиколлинеарности. Для этого построим матрицу парных коэффициентов корреляции между факторными признаками. Получим матрицу парных коэффициентов корреляции в следующем виде: Таблица 1  Проанализируем рассчитанные парные коэффициенты корреляции между факторными признаками. Можно заметить, что между признаками Y1 и Х5, Y3 и X6 существует достаточно тесная линейная зависимость, т.к. коэффициент корреляции между ними составляет 0,9226>0,7 и 0,8429>0,7 . Следовательно, можно сделать вывод о наличии мультиколлинеарности в объясняющих переменных. Для ее устранения необходимо исключить из анализа одну из каждой пары переменных Y1 или Х5, и Y3 или X6, обычно ту, которая имеет наименьшую связь с результативным признаком Y. Наименее тесно с Y связаны признаки X5 и X6. Следовательно, из таблицы первоначальных данных удаляем столбцы X5 и X6. Далее строим новую корреляционную матрицу: Таблица 2  Анализируем новые коэффициенты корреляции. Поскольку значения парных коэффициентов корреляции между объясняющими переменными Y1, Y3, Y4 не превышает по модулю 0,7, следовательно можем перейти к построению модели регрессии. Построение регрессионной модели и ее интерпретация I ЭТАП РЕГРЕССИОННОГО АНАЛИЗА:    Оценка уравнения регрессии имеет вид: Y=-2586,34+4,09Y1+0,082Y3-0,081Y4 Далее необходимо проверить значимость полученных коэффициентов регрессии и уравнения регрессии в целом.. Проверку осуществим на уровне значимости α = 0,05, для чего проверим гипотезу о незначимости построенного уравнения регрессии. Рассчитаем критическое значение F-статистики с помощью встроенной статистической функции FРАСПОБР для уровня значимости α = 0,05 и числа степеней свободы числителя ν1 = k = 3 и знаменателя ν2 = n – k – 1 = 57-3-1=53. Получаем Fкр = 2,779114345. Значение Fнабл=54,82796558 указывается в таблице Дисперсионный анализ в столбце F. Т.к. наблюдаемое значение F-статистики превосходит ее критическое значение Fнабл = 54,82796558 > Fкр = 2,779114345, то гипотеза о незначимости построенного уравнения регрессии отвергается с вероятностью ошибки, равной 0,05. Следовательно, хотя бы один элемент вектора коэффициентов регрессии b значимо отличается от нуля. Проверим далее значимость отдельных коэффициентов уравнения регрессии, т.е. гипотезу H0: b1 = b3 = b4 = 0. Наблюдаемые значения t-статистик tнабл указаны в нижней части таблицы результатов в столбце t-статистика. Откуда видно, что tb1 =8,8731, tb3 = 2,9794, tb4 = -1,8362. Расчетные значения t-статистик необходимо сравнить с критическим значением tкр, найденным для уровня значимости α и числа степеней свободы ν = n – k – 1. Для расчета tкр используем встроенную статистическую функцию MS Excel СТЬЮДРАСПОБР, введя в открывшееся меню функции вероятность α = 0,05 и число степеней свободы ν = n – k – 1 = 57 – 3 – 1 = 53. Получаем tкр = 2,0057. Сравнив расчетные значения t-статистик с критическим, получаем, что для b1 и b3 расчетные (наблюдаемые) значения по модулю превосходят критическое: tb1=8,8731>tкр=2,0057, tb3=2,9794>tкр=2,0057 Следовательно гипотеза о равенстве нулю этих коэффициентов отвергается с вероятностью ошибки, равной 0,05, т.е. соответствующие коэффициенты значимы. tb4=|-1,836217062| Следовательно гипотеза H0 не отвергается, т.е. параметр b4 незначим. Как видно из таблицы для коэффициента b4 p-значение превышает критический уровень в 0,05 и доверительный интервал включает ноль, т.е. по всем проверочным критериям этот коэффициент считается незначимым. Таким образом удаляем столбец Y4. II ЭТАП РЕГРЕССИОННОГО АНАЛИЗА:    Оценка уравнения регрессии имеет вид: Y=-3139,84+4,23Y1+0,047Y3 Проверим на уровне α = 0,05 значимость уравнения регрессии. Для этого в результатах дисперсионного анализ находим наблюдаемое значение F-статистики: Fнабл = 77,1669. Рассчитаем критическое значение F-статистики с помощью встроенной статистической функции FРАСПОБР для уровня значимости α = 0,05 и числа степеней свободы числителя ν1 = k = 2 и знаменателя ν2 = n – k – 1 = 57 – 2 – 1 = 54. Получаем Fкр = 3,1682. Fнабл=77,167>Fкр=3,168, гипотеза о незначимости построенного уравнения регрессии отвергается с вероятности ошибки, равной 0,05. Следовательно, хотя бы один элемент вектора коэффициентов регрессии b значимо отличается от нуля. Проверим далее значимость отдельных коэффициентов уравнения регрессии, т.е. гипотезу H0: b3 = b4 = 0. Наблюдаемые значения t-статистик tнабл указаны в нижней части таблицы результатов в столбце t-статистика. Откуда видно, что tb1 = 9,1206, tb3 = 2,3095. Расчетные значения t-статистик необходимо сравнить с критическим значением tкр, найденным для уровня значимости α и числа степеней свободы ν = n – k – 1. Для расчета tкр используем встроенную статистическую функцию MS Excel СТЬЮДРАСПОБР, введя в открывшееся меню функции вероятность α = 0,05 и число степеней свободы ν = n – k – 1 = 57 – 2 – 1 = 54. Получаем tкр = 2,0049. tb1=9,1206>tкр=2,0049, tb3=2,3095>tкр=2,0049 Следовательно, гипотеза о равенстве нулю этих коэффициентов отвергается с вероятностью ошибки, равной 0,05, т.е. соответствующие коэффициенты значимы Окончательная оценка уравнения регрессии: Y=-3139,84+4,23Y1+0,047Y3 Из таблицы видно, что интервальные оценки для генеральных коэффициентов регрессии имеют вид: 3,3028 Интерпретация результатов: Из таблицы регрессионная статистика следует, что 74,08% вариации Y2-фактической стоимости введенной в отчетном году жилой площади для застройщика, объясняется вариацией ввода общей площади жилых домов (Y1) и общей стоимости реализуемых инвестиционных проектов (Y3). Оставшиеся 25,92% вариации Y объясняются вариацией прочих, неуточненных в модели и случайных факторов. Так как значение R2 близко к единице, можно сделать вывод, что модель достаточно адекватно отражает исследуемый процесс. Коэффициент регрессии при Y1 показывает, что при вводе бщей площади жилых домов на 1 кв.м. фактическая стоимость введенной в отчетном году жилой площади для застройщика увеличивается в среднем на 4233руб. Коэффициент регрессии при Y3 показывает, что при увеличении общей стоимости реализуемых инвестиционных проектов на 1 тыс.руб. фактическая стоимость введенной в отчетном году жилой площади для застройщика увеличивается в среднем на 47руб. Сравнение исходных данных с предсказанными по уравнению регрессии: 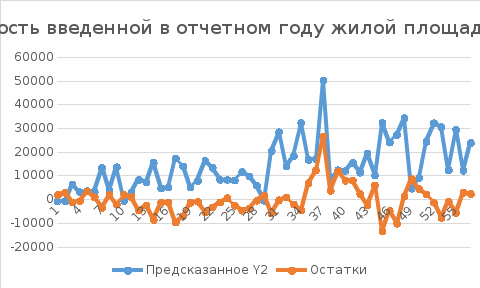 |
