Матеша. Практическая математика. Задача Модель Интерпретация модели
 Скачать 81.55 Kb. Скачать 81.55 Kb.
|
|
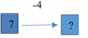
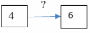
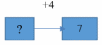
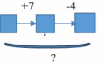
Задание 1. (Максимальное количество баллов – 3 балла) Заполните позицию «Необходимо определить» в графе «Интерпретация модели» таблицы «Виды моделирования при решении текстовых задач». Таблица – «Виды моделирования при решении текстовых задач»
Задание 2. (Максимальное количество баллов – 3 балла) Решите задачу, используя диаграммы Эйлера-Венна. При выборе кружков для детей оказалось, что 60 % родителей желают, чтобы их ребенок посещал кружок рисования, 50 % предпочли занятия по гимнастике, 50% отметили, что выбрали бы занятия музыкой. При этом 30 % родителей предпочитают, чтобы их дети посещали занятия и по рисованию, и по гимнастике, 20 % сделали выбор в пользу занятий по гимнастике и музыке, а 40 % родителей пожелали бы, чтобы ребенок рисовал и занимался хоровым пением, и только 10 % из них высказались за посещение детьми всех кружков. Определите процентное соотношение родителей, которые: 1) не желают водить детей в кружки; 2) выбрали не менее двух кружков. Задание 3 (максимальное количество баллов – 5 баллов) При измерении получены данные:
Выполните задания с учетом исходных данных, подробно описывая ход решения. а) Постройте статистический ряд распределения частот. б) Постройте полигон распределения. в) Вычислите выборочную среднюю, дисперсию, моду, медиану. г) Постройте выборочную функцию распределения. Задание 4 (максимальное количество баллов - 4 балла) Решите примеры, связанные с погрешностями, подробно описывая ход решения. a) Округлите число 4,45575250 до шести, пяти, четырех, трех, двух и одного десятичных знаков; до целого числа. b) Число 12,75 определено с относительной погрешностью 0,3, %. Найдите абсолютную погрешность округления. c) Определите верные и сомнительные цифры числа 13,27 ± 0,03. Задание 5 (максимальное количество баллов – 3 балла) Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением. На стороне AC треугольника ABC отмечена точка D так, что AD=3см, DC=10см. Площадь треугольника ABC равна 39 см2. Найдите площадь треугольника ABD. Задание 6 (максимальное количество баллов – 4 балла) Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением. Биссектриса угла A параллелограмма ABCD пересекает его сторону BC в точке F. Найдите площадь параллелограмма ABCD, если BF=4 см, FC=2 см, а угол ABC равен 1500. Задание 7 (максимальное количество баллов – 3 балла) Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 см и 8 см, а боковое ребро призмы равно 12 см. |