Анализ инвестиционных проектов. Анализа инвестициоННых проектов Модели анализа основных финансовых операций Пусть p начальный капитал, положенный в банк при год

• Название: Анализа инвестициоННых проектов Модели анализа основных финансовых операций Пусть p начальный капитал, положенный в банк при год
• Дата: 14.10.2021
• Размер: 317 Kb.
• Имя файла: Анализ инвестиционных проектов.doc
• Тип: Документы; #247437

модели и методы анализа инвестициоННых проектов
1. Модели анализа основных финансовых операций
Пусть P – начальный капитал, положенный в банк при годовой процентной ставке r. Тогда в конце периода капитализации наращенная сумма, т.е. сумма начального капитала и наросшего процента, составит , где r выражена в долях. В конце второго периода капитализации наращенная сумма составит . В общем случае, сумма, наращенная за n периодов капитализации, составит:
. (1)
Наращенная сумма называется будущей стоимостью начального капитала и обозначается FV (futurevalue).
Коэффициент называется коэффициентом аккумуляции, который показывает денежную сумму, нарастающую за n периодов капитализации при начальном капитале 1 ден.ед.
Пример:P=1000 ден.ед., r=12%, n=3. Наращенная сумма составит ден.ед. Коэффициент аккумуляции показывает, что при годовой процентной ставке 12% с одной денежной единицы, положенной в банк, за три года нарастает 1,405 ден.ед.
Из формулы (1) следует, что , т.е., для того, чтобы сумма, наращенная за n периодов капитализации, составила S ден.ед., нужно положить в банк в начале срока ден.ед. Такой начальный капитал, обеспечивающий заданную наращенную сумму, называется текущей стоимостью суммы S и обозначается PV (presentvalue):
. (2)
Процесс нахождения текущей стоимости называется дисконтированием.
Коэффициент называется коэффициентом дисконтирования, который показывает, какую сумму нужно положить в банк для того, чтобы через n периодов капитализации наращенная сумма составила 1 ден.ед.
Пример: Для того, чтобы сумма, наращенная заn=5 лет, при годовой процентной ставке r=12% составила S=1000 ден.ед. в начале срока нужно положить в банк ден.ед. Коэффициент дисконтирования равен .
2. Модели анализа эффективности инвестиционных проектов (ИП)
2.1. Текущая стоимость инвестиционного проекта
Под инвестиционным проектом будем понимать любое инвестирование денег, генерирующее денежные потоки в будущем.

Метод дисконтирования денежных потоков ИП является ключевым в современном финансовом анализе. Дисконтируются свободные денежные потоки, которые представляют собой разность прибыли и инвестиций в заданном периоде времени: , где – свободный денежный поток в k–м периоде, – прибыль в k–м периоде, – инвестиции в k–м периоде.
Пусть инвестиционный проект генерирует положительные свободные денежные потоки в течение n периодов времени: , , …, . Начальные инвестиции в проект равны . Временную диаграмму свободных денежных потоков можно представить в виде:

Свободные денежные потоки	–			…
	|------------|------------|-------------------------|------------|--->
Годы	0	1	2		n–1	n

Знак «–» перед начальными инвестициями показывает, что это расходы, а не доходы.
Вместо того, чтобы инвестировать деньги в проект, инвестор может положить некоторую сумму в банк под процент с целью получения таких же денежных платежей в будущем.
Текущей стоимостьюсвободных денежных потоков ИП называется начальный капитал, положенный в банк под процент, обеспечивающий последовательность денежных платежей, равных свободным денежным потокам проекта:
, (3)
где r – банковская процентная ставка для одного периода капитализации.

Таким образом, текущая стоимость инвестиционного проекта представляет собой сумму дисконтированных денежных потоков.
Процентная ставка, используемая при дисконтировании свободных денежных потоков ИП, называетсянормой (ставкой)дисконтирования.

В качестве нормы дисконтирования можно брать банковскую процентную ставку только в случае, когда риск, связанный с денежными потоками проекта, и риск, связанный с банковскими депозитами, одинаков.
Пример: Проект требует 600 ден.ед. начальных инвестиций. За первый год свободный денежный поток составит 300 ден.ед., за второй год 500 ден.ед. Определить текущую стоимость проекта при банковской процентной ставке 12%.

Св. ден. потоки	–600 ден.ед.	300 ден.ед	500 ден.ед
|------------------|-----------------|------------->
Годы	0	1	2

ден.ед.
Таким образом, чтобы получить через год платеж в размере 300 ден.ед., а через два 500 ден.ед. на банковский депозит под 12% годовых требуется положить 666,45 ден.ед.

2.2. Чистая текущая стоимость ИП
Проанализируем выгодность инвестирования денег в проект по сравнению с вложением в банк.

Чистая текущая стоимость NPV (netpresentvalue) инвестиционного проекта представляет собой разность между текущей стоимостью проекта и начальными инвестициями и показывает, на сколько меньше денежных единиц необходимо вложить в начальный момент времени в проект чем в банковский депозит для того, чтобы обеспечить последовательность денежных платежей, равных свободным денежным потокам проекта:
. (4)
Если NPV>0, то проект эффективен, если NPV<0, то проект неэффективен, если NPV=0, то следует использовать другие критерии эффективности.
Пример: На основе предыдущего примера найти чистую текущую стоимость инвестиционного проекта. PV=666,45 ден.ед., =600 ден.ед.

=666,45–600=66,45 ден.ед. Следовательно, начальные инвестиции в проект на 66,45 ден.ед. меньше, чем банковcкий депозит, обеспечивающий последовательность платежей, равных свободным денежным потокам инвестиционного проекта.
2.3. Внутренняя норма прибыли инвестиционного проекта
Внутренняя норма прибыли IRR (internalrateofreturn) инвестиционного проекта – это такая банковская процентная ставка, при которой банковский начальный капитал, обеспечивающий последовательность денежных платежей, равных свободным денежным потокам проекта, равен начальным инвестициям в проект, т.е. это такая ставка дисконтирования свободных денежных потоков проекта, при которой его чистая текущая стоимость равна нулю. Из данного определения и формул (3) и (4) непосредственно вытекает, что IRR есть решение уравнения:
. (5)
Если IRR>r, то проект следует принять, если IRR<r– проект следует отвергнуть, если IRR=r – инвестиции в проект окупаются.

В общем случае в качестве нормы дисконтирования денежных потоков проекта нужно брать внутреннюю норму прибыли альтернативных проектов с таким же финансовым риском, как и у данного проекта.
Пример: На основе предыдущего примера найти внутреннюю норму прибыли инвестиционного проекта: =600 ден.ед., =300 ден.ед., =500 ден.ед.

Подставим в уравнение (5):
IRR=19,64% ,
следовательно, банковский начальный капитал в 600 ден.ед., который равен начальным инвестициям в проект, обеспечит выплату платежей, равных свободным денежным потокам инвестиционного проекта при годовой процентной ставке 19,64%.

2.4. Индекс прибыльности
Индекс прибыльностиPI (profitabilityindex)оценивает относительную прибыльность ИП, т.е. прибыльность с каждой вложенной денежной единицы:
. (6)
При PI>1 – проект эффективен, при PI<1 – проект неэффективен, при PI=1 – необходимо использовать другие методы оценки. Чем больше значение индекса прибыльности, тем выше прибыль с каждой денежной единицы.
2.5. Период окупаемости
Период окупаемости PP (paybackperiod) ИП определяется следующим образом:
, при котором . (7)
Дисконтированный период окупаемости DPP:
, при котором . (8)
Всегда DPP>PP, т.е. проект, приемлемый по критерию PP, может оказаться неприемлемым по критерию DPP.
3. Влияние инфляции на денежные потоки проекта
Предположим, что потребительская корзина состоит из m видов благ (товаров и услуг). Пусть – количество k–го блага в потребительской корзине, – рыночная цена единицы k–го блага в начале периода времени, – рыночная цена единицы k–го блага в конце периода. Тогда цены потребительской корзины в начале и конце периода будут равны:
, .
Уровень инфляции за период будет определяется по формуле: .

Пусть P – начальный капитал, аr – банковская процентная ставка за период времени. Тогда в конце периода наращенная сумма составит:
.
Процентную ставку r называют номинальной.

В начале периода за начальный капитал можно купить потребительских корзин, а в конце периода за наращенную сумму .

Реальная процентная ставкаопределяется по формуле и показывает, на сколько процентов больше можно купить потребительских корзин в конце периода за наращенную сумму, чем в начале за начальный капитал. В отличие от номинальной процентной ставки реальная процентная ставка учитывает инфляцию.

Найдем, как реальная процентная ставка определяется с помощью номинальной процентной ставки и уровнем инфляции:
.
Пример: Пусть номинальная годовая процентная ставка равна r=36%, а годовой уровень инфляции составляет i=20%. Найти реальную процентную ставку.
.
Инфляция влияет на внутреннюю норму прибыли ИП, поэтому при нахождении чистой текущей стоимости проекта надо учитывать инфляцию.

Номинальная процентная ставка находится с помощью реальной процентной ставки и уровня инфляции следующим образом:
.
Данную формулу можно использовать для определения нормы дисконтирования свободных денежных потоков проекта.
Пример: Если внутренняя норма прибыли без учета инфляции альтернативных проектов равна IRR=14%, а годовой уровень инфляции i=20%, то ставка дисконтирования составит r=0.14+0.2+0,028=0,368 или 36,8%.
4. Модель оптимального портфеля инвестиционных проектов
Рассмотрим возможность реализации n инвестиционных проектов. Эффективность i–го инвестиционного проекта характеризуется чистой текущей стоимостью проекта , . Первоначальные инвестиции для реализации i–го проекта составляют , . Размер имеющихся в распоряжении финансовых ресурсов равен .

Пусть – решение о реализации либо отклонении i–го проекта, принимающее следующие значения:

Таким образом, ЭММ оптимального портфеля инвестиционных проектов имеет вид:

maxF= ,	– максимум доходности портфеля инвестиционных проектов,
,	– ограничения на финансовые ресурсы,
	– ограничения на значения переменных.

5. Анализ чувствительности денежных потоков ИП
Анализ чувствительности денежных потоков ИП – это анализ того, как изменятся денежные потоки проекта при изменении одного или нескольких влияющих на них факторов.
Рассмотрим методику анализа чувствительности на примере.
Пример: Автомобильная компания рассматривает проект производства нового автомобиля. Начальные инвестиции 40 млн.ден.ед. Проект рассчитан на n=5 лет. Планируемый выпуск автомобилей Q=10000 в год, ожидаемая цена одного автомобиля p=11000 ден.ед., переменные издержки в расчете на один автомобиль v=9000 ден.ед., постоянные издержки F=5 млн.ден.ед. в год. Налог на прибыль равен t=40%. Норма дисконтирования денежных потоков проекта r=14%. Будем считать, что инфляция отсутствует.

Решение:Прибыль проекта до уплаты налога за год равна:
млн.ден.ед.
Будем считать, что налог уплачивается в конце года с разности между прибылью и амортизацией, если эта разность положительна. Предположим, что годовая амортизация находится как отношение начальных инвестиций к сроку проекта, т.е. млн.ден.ед.

Тогда бухгалтерская налогооблагаемая прибыль составит:
млн.ден.ед.
Налог равен млн.ден.ед., если выражение в скобках положительно, и равен нулю, если оно меньше либо равно нулю.
Прибыль после уплаты налога будет равна: 15–2,8=12,2 млн.ден.ед.

Формула для нахождения годового денежного потока будет иметь вид: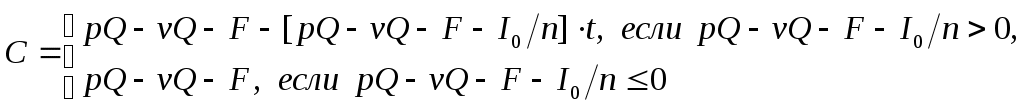
(9)
Построим временную диаграмму:

Свободные денежные потоки	–40	12,2	12,2	12,2	12,2	12,2
Годы	0	1	2	3	4	5

Найдем чистую текущую стоимость проекта:
ден.ед.
ден.ед. означает, что начальные инвестиции в данный проект на 1883588 ден.ед. меньше, чем начальные инвестиции в альтернативные проекты, обеспечивающие такую же последовательность денежных потоков, как и рассматриваемый проект, т.е. 12,2 млн.ден.ед. в год в течение пяти лет.

Внутренняя норма прибыли:
, , IRR =15,94%.
На практике параметры модели могут изменяться, поэтому важно знать, как изменяться денежные потоки при отклонении параметров от своих ожидаемых значений.

Предположим, что количество выпускаемых в год автомобилей является переменным параметром модели, а все остальные являются постоянными. Тогда формула (9) примет вид:

После преобразований: (10)
Данную зависимость можно изобразить графически:

Обозначим , где – начальное, а – конечное значение параметра Q, а через , где значения и соответствуют и . Из формулы (10) следует, что :
(11)
Из (11) можно сделать вывод, что при увеличении годового выпуска продукции на одну единицу прибыль увеличится на 1200 ден.ед., если налогооблагаемая прибыль положительна, и на 2000 ден.ед. в противном случае.

Формулу (11) можно получить из (9) с помощью частной производной от денежного потока по объему производства: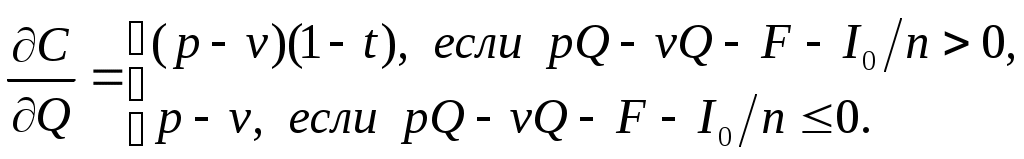
(12)
Из полученной формулы следует:
(13)
Сравнив (11) и (13), можно сделать вывод, что частная производная показывает, на сколько денежных единиц изменится денежный поток при увеличении годового выпуска продукции на одну единицу, т.е.
(14)
при достаточно малом .

Аналогично можно найти частные производные от денежного потока по другим параметрам: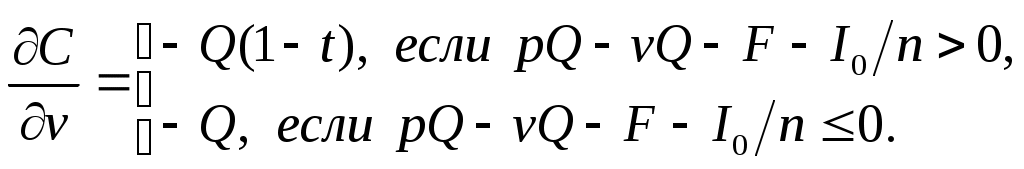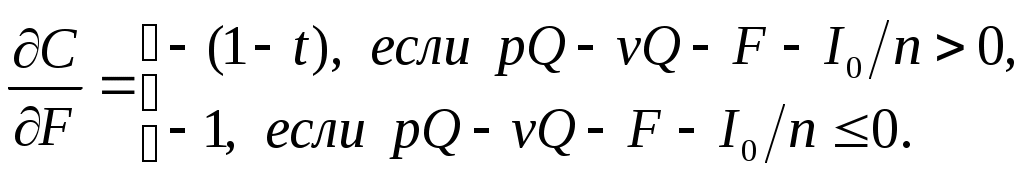









Экономический смысл этих частных производных такой же как у .

Особого внимания заслуживает частная производная по налоговой ставке, поскольку налоговая ставка измеряется в процентах, т.е. в сотых долях. Для изменения денежного потока при изменении налоговой ставки формула (14) примет вид:
(15)
Предположим, что налоговая ставка увеличилась на один процент, т.е. , тогда используя формулу (15) получим, что денежный поток изменится на ден.ед. В нашем примере млн. Это значит, что при увеличении процентной ставки на 1% денежный поток уменьшится на 70000 ден.ед., так как .

При одновременном изменении нескольких параметров соответствующее изменение денежного потока определяется по формуле:

Отметим, что анализ чувствительности можно проводить и для чистой текущей ценности и внутренней нормы прибыли.

В примере предполагалось, что уровень инфляции равен нулю. При ненулевом уровне инфляции анализ модели изменился бы следующим образом.

Обозначим уровень инфляции через i. Тогда цена единицы продукции в конце k–го года будет равняться 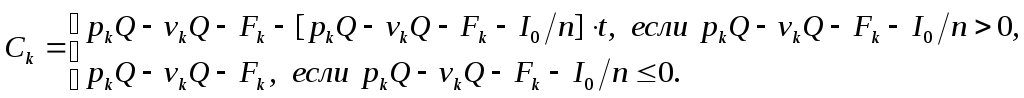, где – цена единицы продукции в начальный момент времени. В этом случае денежный поток в k–м году вычисляется по формуле:
(16)
Пусть i=20% , по формуле (16) можно определить годовые потоки с первого по пятый годы: 14000 тыс.ден.ед., 16160 тыс.ден.ед., 18752 тыс.ден.ед., 21862 тыс.ден.ед., 25595 тыс.ден.ед.
Временная диаграмма денежных потоков будет иметь вид:

Свободные ден. потоки	–40000	14000	16160	18752	21862	25595
Годы	0	1	2	3	4	5

Определим внутреннюю норму прибыли проекта:
(17)
Решив это уравнение, получим IRR=33,936%.

Выше было показано, что . Эту формулу можно использовать для определения дисконтирования денежных потоков проекта. Например, если реальная доходность альтернативных проектов =14%, а i=20%, то норма дисконтирования r=0,368, или 36,8%, и чистая текущая величина проекта составит:


тыс.ден.ед.

МОДЕЛИ И МЕТОДЫ АНАЛИЗА ИНВЕСТИЦИОННЫХ ПРОЕКТОВ