Отчет по контрольной работе Анализ точности механической обработки методом кривых распределения 3 вариант. Анализа точности механической обработки методом кривых распределения Оценить вероятность получения год
 Скачать 240.41 Kb. Скачать 240.41 Kb.
|
|
Построение эмпирической кривой распределения Определение размаха выборки 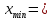 9,83 9,83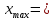 10,09 10,09R = 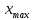 - - 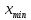 = 10,09 – 9,83 = 0,26 = 10,09 – 9,83 = 0,265.1 Определение величины интервала Δx = 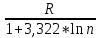 = =  = 0,016 = 0,016Округляем Δx в большую сторону до величины, кратной цене деления микрометра: Δx = 0,02 5.2 Определение границ интервалов 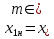 - - 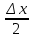 = 9,83 – 0,01 = 9,82 = 9,83 – 0,01 = 9,82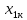 = = 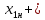 Δx = 9,82 + 0,02 = 9,84 Δx = 9,82 + 0,02 = 9,84
Таблица 2 5.3 Графическое оформление результатов измерений Строим гистограммы по результатам измерений, записанных в таблице 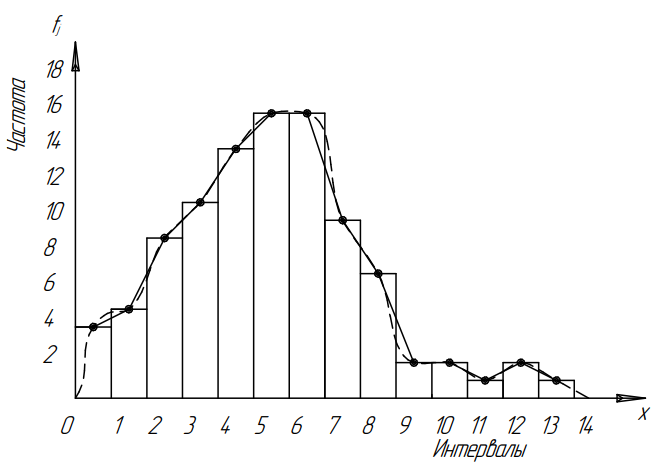 Рисунок 5. 6. Расчет среднего арифметического значения и квадратического отклонения размеров Графическая интерпретация полученных результатов позволяет сделать вывод, что размеры деталей группируются около некоторой центральной величины. ; 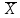 = = 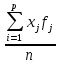
Таблица 3 Для упрощения расчетов воспользуемся формулой: 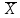 = a + Δx = a + Δx 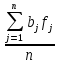 = 9,93 = 9,93Сейчас посчитаем среднеквадратическое отклонение: σ = 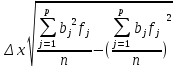 = 0,053591 = 0,053591Теоретическая кривая распределения Если постепенно увеличивать размер партии, то эмпирическая кривая распределения будет приближаться по форме к холмообразной кривой, представленной штриховой линией на рис. 5, а частота 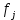 и частность и частность 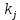 на каждом интервале будут стремиться к некоторым значениям на каждом интервале будут стремиться к некоторым значениям 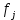 и и 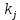 на данном интервале, которые называются теоретической частотой и теоретической частостью. Очевидно, что в пределе при n = ∞ на данном интервале, которые называются теоретической частотой и теоретической частостью. Очевидно, что в пределе при n = ∞ 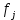 = =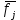 , , 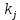 = =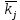 и дискретная случайная величина и дискретная случайная величина 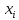 становится непрерывной случайной величиной x. График зависимости становится непрерывной случайной величиной x. График зависимости 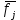 или или 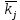 от x называется теоретической кривой распределения. от x называется теоретической кривой распределения.Закон нормального распределения Плотность распределения случайной величины по нормальному закону, или плотность нормального распределения:  Физический смысл плотности распределения можно представить как вероятность появления случайной величины в окрестности некоторой точки на бесконечно малом отрезке числовой оси x. В окрестности x = 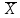 плотность распределения максимальна, т.е. вероятность появления случайной величины в окрестностях этой точки наибольшая. С увеличением разности (x- плотность распределения максимальна, т.е. вероятность появления случайной величины в окрестностях этой точки наибольшая. С увеличением разности (x-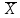 ) плотность распределения уменьшается. ) плотность распределения уменьшается.  Рисунок 6. Интеграл вероятности: 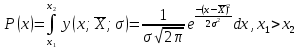 Физический смысл – он позволяет определить вероятность появления случайной величины xв некотором интервале  , с плотностью распределения по нормальному закону. , с плотностью распределения по нормальному закону.Геометрический смысл – площадь под кривой нормального распределения в пределах заданного интервала Для узкого интервала, тогласно теореме о среднем, интеграл вероятности выглядит следующим образом: 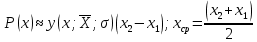 Нормирование распределения Формула нормированной переменной: ɀ = (x – 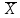 ) / ) / 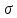 плотность вероятности нормированного распределения: 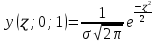 И, соответственно, интеграл вероятности: 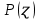 = = 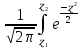 d d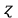 Процедура нормирования приводит множество кривых распределения к одной кривой, зависящей только от нормированной переменной. В результате происходит совмещение центра группирования с началом новой системы координат ( 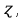 y), и кривая нормированного нормального распределения становится симметричной отно/сительно оси координат. y), и кривая нормированного нормального распределения становится симметричной отно/сительно оси координат.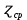 = 0; = 0; 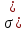 ɀ) = 1. ɀ) = 1. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||