Отчет по контрольной работе Анализ точности механической обработки методом кривых распределения 3 вариант. Анализа точности механической обработки методом кривых распределения Оценить вероятность получения год
 Скачать 240.41 Kb. Скачать 240.41 Kb.
|
|
Функция Лапласа Функция Лапласа: Ф(ɀ) = 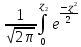 dɀ dɀФизический смысл – определяет вероятность появления случайной величины. Геометрический смысл – площадь заштрихованной фигуры под кривой нормированного нормального распределения на интервале изменения нормированной переменной от 0 до 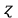 . .На практике функция Лапласа позволяет вычислить теоретические частость и частоту. 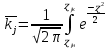 = = 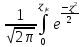 - - 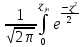 = Ф( = Ф(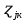 ) - Ф( ) - Ф( ) )И, соответственно, согласно теореме о среднем приближенном: 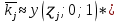 Δ Δ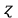 ; ; 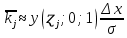 ; ; 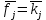 * n * nПостроение теоретической кривой распределения Уравнение нормированной переменной в середине интервала для плотности вероятности: 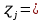 ( (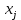 – – 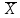 ) / ) / 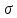
Таблица 4  Рисунок 7. Теоретическая кривая распределения размеров Критерии для оценки точности механической обработки Оценка точности механической обработки проводится путем сопоставления величины и расположения поля допуска размера T c величиной и расположением поля рассеяния размеров 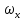 для теоретической кривой нормального распределения. для теоретической кривой нормального распределения. Установлено, что если случайная величина подчиняется нормальному закону распределения, то вероятность появления её в интервале 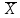 - - 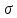 < x < < x <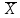 + + 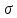 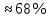 ; ;В интервале 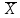 - 2 - 2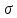 < x < < x <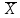 + + 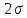  ; ;И, в интервале 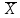 - 3 - 3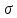 < x < < x <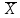 + +  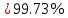 . .Следовательно, вне последнего интервала, вероятность составляет <0,3%. По этому при механической обработке принимают: 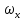 = = 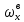 - -  , где: , где: = = 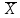 - 3 - 3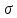 = 9,769 - нижнее граничное поле рассеяния; = 9,769 - нижнее граничное поле рассеяния;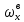 = = 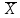 + 3 + 3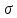 = 10,09 - верхнее граничное поле рассеяния. = 10,09 - верхнее граничное поле рассеяния.Таким образом ширина кривой нормального распределения = 6 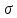 – это и называют правилом “шести сигм”. – это и называют правилом “шести сигм”.Условие оценки точности: при отсутствии брака поле рассеяния размеров находится в пределах поля допуска. Выполним проверку условий: Поле рассеяния размера меньше допуска, или равно ему: 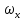 = 0,32 = 0,32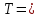 0,15 0,15Следовательно, 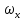 > T => первое условие НЕ выполняется. Значит обе ветви кривой распределения будут выходить за пределы поля допуска. > T => первое условие НЕ выполняется. Значит обе ветви кривой распределения будут выходить за пределы поля допуска.Данное неравенство называют необходимым условием. нижнее граничное значение поля рассеяния больше наименьшего предельного размера или равно ему:  = 9,77 = 9,77 = 9,85 = 9,85Значит,  < < , и мы видим, что и второе условие НЕ выполняется , и мы видим, что и второе условие НЕ выполняетсяЗначит левая ветвь кривой распределения выходит за пределы поля допуска. Верхнее граничное значение поля рассеяния меньше наибольшего предельного размера, или равно ему: 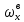 = 10,09 = 10,09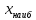 = 10,0 = 10,0Мы видим, что 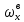 > >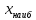 => и это условие НЕ выполняется. => и это условие НЕ выполняется.Значит правая ветвь кривой распределения выходит за пределы поля допуска. Последние 2 пункта – достаточные условия. Так как все наши условия НЕ выполняются, то мы должны учитывать, что в нашем случае существует вероятность получения бракованной продукции. 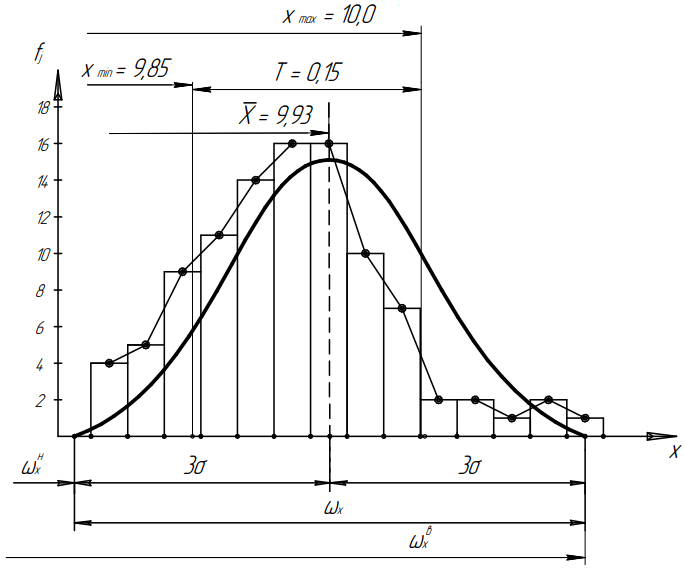 Рисунок 8 Оценка вероятности получения годных и бракованных деталей Вычислим значения нормированных переменных для наименьшего и наибольшего предельного размера образцов: 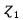 = = 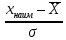 = = = = 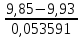 = -1,49 = -1,49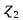 = = 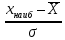 = = = = 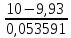 = 1,31 = 1,31Далее, определяем значение функции Лапласа для этих значений: Ф( 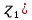 = -0,4320 = -0,4320Ф( 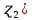 = 0,4050 = 0,4050Определяем вероятность получения годных деталей, размеры которых находятся в поле допуска:  Ф( Ф(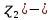 Ф( Ф(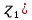 ]*100 = (0,4050 + 0,4320)*100 = 83,7% ]*100 = (0,4050 + 0,4320)*100 = 83,7%Далее, определим вероятность получить бракованных деталей, размеры которых находятся за пределами поля допуска:  = [0,5 + Ф( = [0,5 + Ф(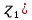 ]*100 -= (0,5 -0,4320)*100 = 6,8% ]*100 -= (0,5 -0,4320)*100 = 6,8%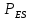 = [0,5 - Ф( = [0,5 - Ф(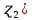 ]*100 -= (0,5 -0,4050)*100 = 9,5% ]*100 -= (0,5 -0,4050)*100 = 9,5%Вывод: Детали, которые выходят за нижнюю границу ei поля допуска в количестве 6,8% являются неисправимым браком. Детали, размеры которых выходят за верхнюю границу es поля допуска в количестве 9,5% - являются исправимым браком. |
