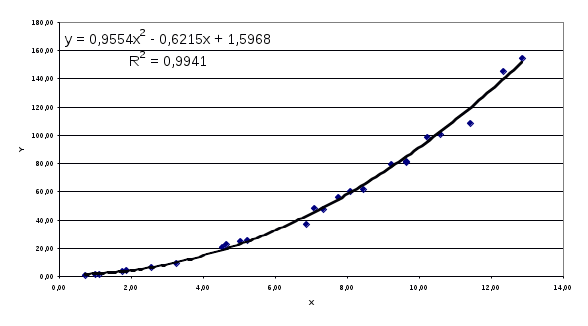4. Построение графиков в Excel и использование функции ЛИНЕЙН.
Рассмотрим результаты эксперимента, приведенные в исследованном выше примере.
Исследуем характер зависимости в три этапа:
Построим график зависимости.
Построим линию тренда (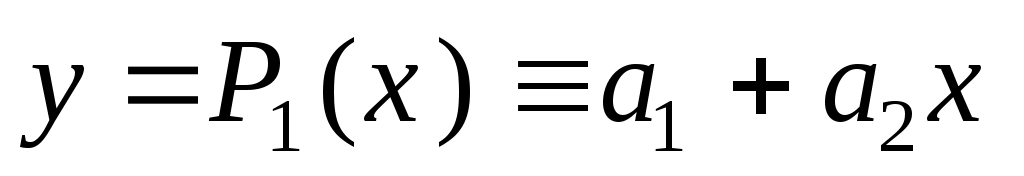 , , 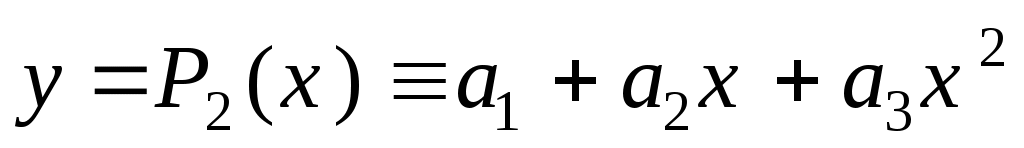 , , 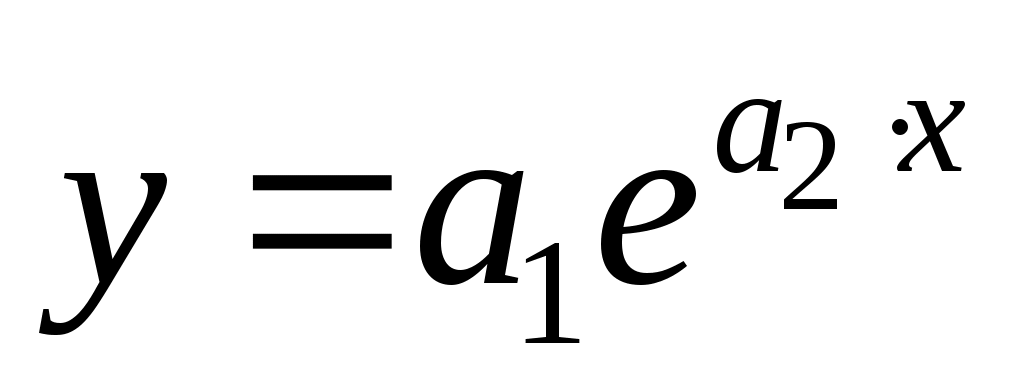 ). ).
Получим числовые характеристики коэффициентов этого уравнения.
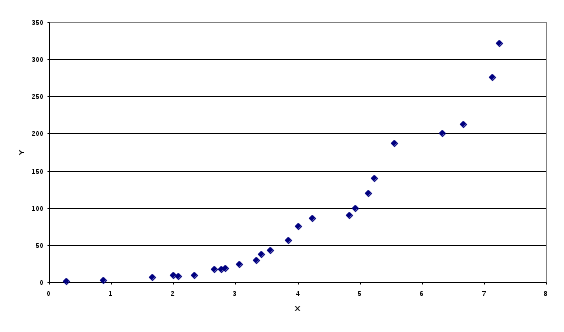
Рис.4.1. График зависимости y от x
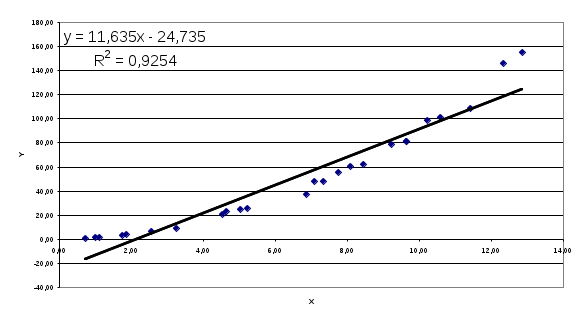
Рис.4.2. График линейной аппроксимации
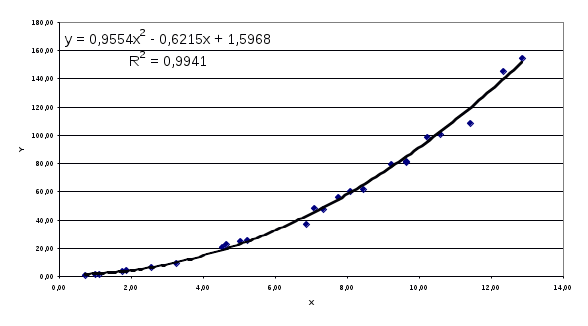
Рис.4.3. График квадратичной аппроксимации.
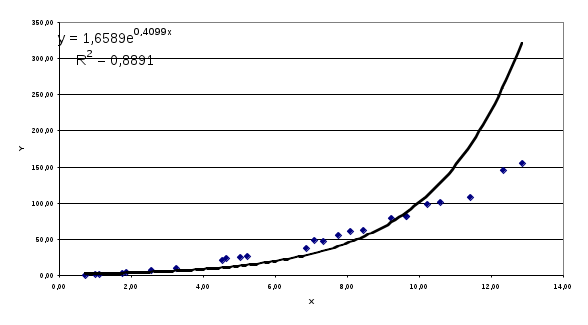
Рис.4.4. График экспоненциальной аппроксимации.
Примечание: Полученное при построении линии тренда значение коэффициента детерминированности для экспоненциальной зависимости 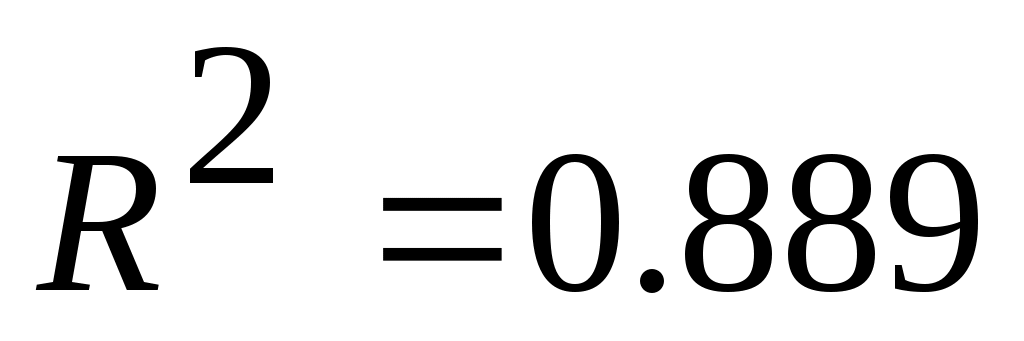 не совпадает с истинным значением не совпадает с истинным значением 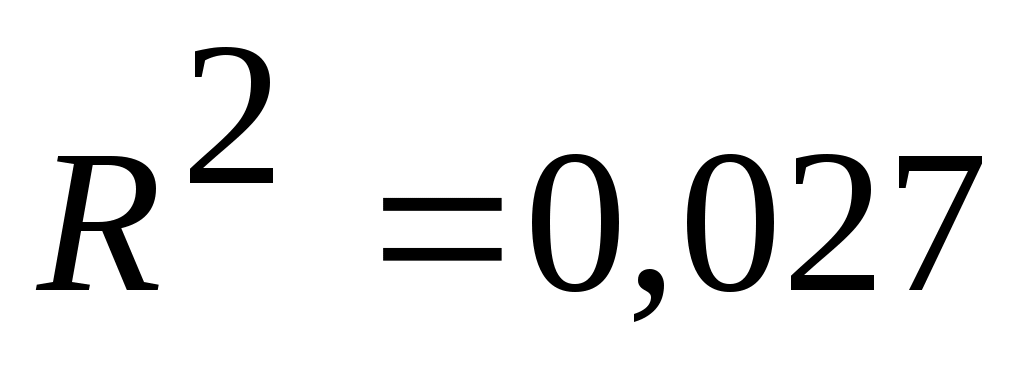 , поскольку при вычислении коэффициента детерминированности используются не истинные значения , поскольку при вычислении коэффициента детерминированности используются не истинные значения 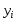 , а преобразованные значения , а преобразованные значения 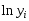 с дальнейшей линеаризацией. с дальнейшей линеаризацией.
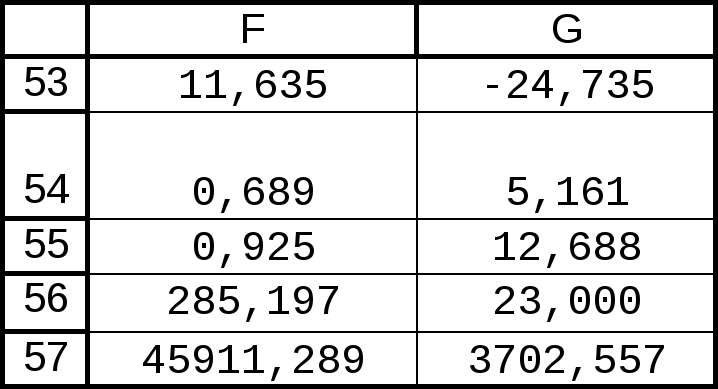
Таблица 9
5. Программа на языке Pascal. 5

Аппроксимация функции y=f(x) линейной, квадратичной и экспоненциальной функциями
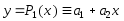 , ,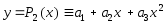 , ,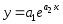 . .
.1. Схема алгоритма.

Рис.5.1. Блок-схема
program Kramer;
uses CRT;
const
n=25;
type
TArrayXY = array[1..2,1..n] of real;
TArray = array[1..n] of real;
var
SumX,SumY,SumX2,SumXY,SumX3,SumX4,SumX2Y,SumLnY,SumXLnY: real;
OPRlin,OPRkvadr,OPRa1,OPRa2,OPRa3:real;
a1lin,a2lin,a1kvadr,a2kvadr,a3kvadr,a1exp,a2exp,cexp:real;
Xsr,Ysr,S1,S2,S3,Slin,Skvadr,Sexp:real;
Kkor,KdetLin,KdetKvadr,KdetExp:real;
i:byte;
const
ArrayXY:TArrayXY=((12.85,12.32,11.43,10.59,10.21,9.65,9.63,9.22,8.44,8.07,7.74,7.32,7.08,6.87,5.23,5.02,4.65,4.53,3.24,2.55,1.86,1.76,1.11,0.99,0.72) , (154.77
145.59,108.37,100.76,98.32,81.43,80.97,79.04,61.76,60.54,55.86,47.63,48.03,36.85,25.65,24.98,22.87,20.32,9.06,6.23,3.91,3.22,1.22,1.10,0.53));
begin
ClrScr;
SumX:=0.0;
SumY:=0.0;
SumXY:=0.0;
SumX2:=0.0;
SumX3:=0.0;
SumX4:=0.0;
SumX2Y:=0.0;
SumLnY:=0.0;
SumXLnY:=0.0;
{ Вычисление сумм x, y, x*y, x^2, x^3, x^4, (x^2)*y, Ln(y), x*Ln(y) }
for i:=1 to n do
begin
SumX:=SumX+ArrayXY[1,i];
SumY:=SumY+ArrayXY[2,i];
SumXY:=SumXY+ArrayXY[1,i]*ArrayXY[2,i];
SumX2:=SumX2+sqr(ArrayXY[1,i]);
SumX3:=SumX3+ArrayXY[1,i]*ArrayXY[1,i]*ArrayXY[1,i];
SumX4:=SumX4+sqr(ArrayXY[1,i])*sqr(ArrayXY[1,i]);
SumX2Y:=SumX2Y+sqr(ArrayXY[1,i])*ArrayXY[2,i];
SumLnY:=SumLnY+ln(ArrayXY[2,i]);
SumXLnY:=SumXLnY+ArrayXY[1,i]*ln(ArrayXY[2,i])
end;
{ Вычисление коэффициентов }
OPRlin:=0.0;
a1lin:=0.0;
a2lin:=0.0;
a1kvadr:=0.0;
OPRkvadr:=0.0;
a2kvadr:=0.0;
a2kvadr:=0.0;
a1exp:=0.0;
a2exp:=0.0;
OPRlin:=n*SumX2-SumX*SumX;
a1lin:=(SumX2*SumY-SumX*SumXY)/OPRlin;
a2lin:=(n*SumXY-SumX*SumY)/OPRlin;
OPRkvadr:=n*SumX2*SumX4+SumX*SumX3*SumX2+SumX2*SumX*SumX3- SumX2*SumX2*SumX2-n*SumX3*SumX3-SumX*SumX*SumX4;
a1kvadr:=(SumY*SumX2*SumX4+SumX*SumX2Y*SumX3+SumX2*SumXY*SumX3- SumX2*SumX2*SumX2Y-SumY*SumX3*SumX3-SumX*SumXY*SumX4)/OPRkvadr;
a2kvadr:=(n*SumXY*SumX4+SumY*SumX3*SumX2+SumX2*SumX*SumX2Y-SumX2*SumX2*SumXY-n*SumX3*SumX2Y-SumY*SumX*SumX4)/OPRkvadr;
a3kvadr:=(n*SumX2*SumX2Y+SumX*SumXY*SumX2+SumY*SumX*SumX3-SumY*SumX2*SumX2-n*SumXY*SumX3-SumX*SumX*SumX2Y)/OPrkvadr;
a2exp:=(n*SumXLnY-SumX*SumLnY)/OPRlin;
cexp:=(SumX2*SumLnY-SumX*SumXLnY)/OPRlin;
a1exp:=exp(cexp);
{ Вычисление средних арифметических x и y }
Xsr:=SumX/n;
Ysr:=SumY/n;
S1:=0.0;
S2:=0.0;
S3:=0.0;
Slin:=0.0;
Skvadr:=0.0;
Sexp:=0.0;
Kkor:=0.0;
KdetLin:=0.0;
KdetKvadr:=0.0;
KdetExp:=0.0;
for i:=1 to n do
begin
S1:=S1+(ArrayXY[1,i]-Xsr)*(ArrayXY[2,i]-Ysr);
S2:=S2+sqr(ArrayXY[1,i]-Xsr);
S3:=S3+sqr(ArrayXY[2,i]-Ysr);
Slin:=Slin+sqr(a1lin+a2lin*ArrayXY[1,i]-ArrayXY[2,i]);
Skvadr:=Skvadr+sqr(a1kvadr+a2kvadr*ArrayXY[1,i]+a3kvadr*ArrayXY[1,i]*ArrayXY[1,i]-ArrayXY[2,i]);
Sexp:=Sexp+sqr(a1exp*exp(a2exp*ArrayXY[1,i])-ArrayXY[2,i]);
end;
{ Вычисление коэффициентов корреляции и детерминированности }
Kkor:=S1/sqrt(S2*S3);
KdetLin:=1-Slin/S3;
KdetKvadr:=1-Skvadr/S3;
KdetExp:=1-Sexp/S3;
{ Вывод результатов }
WriteLn('Линейная функция');
WriteLn('a1=',a1lin:8:5);
WriteLn('a2=',a2lin:8:5);
WriteLn('Квадратичная функция');
WriteLn('a1=',a1kvadr:8:5);
WriteLn('a2=',a2kvadr:8:5);
WriteLn('a3=',a3kvadr:8:5);
WriteLn('Экспоненциальная функция');
WriteLn('a1=',a1exp:8:5);
WriteLn('a2=',a2exp:8:5);
WriteLn('c=',cexp:8:5);
WriteLn('Xcp=',Xsr:8:5);
WriteLn('Ycp=',Ysr:8:5);
WriteLn('Коэффициент корреляции ',Kkor:8:5);
WriteLn('Коэффициент детерминированности (линейная аппроксимация) ',KdetLin:2:5);
WriteLn('Коэффициент детерминированности (квадратическая аппроксимация) ',KdetKvadr:2:5);
WriteLn('Коэффициент детерминированности (экспоненциальная аппроксимация) ',KdetExp:2:5);
end.
5.2. Результаты расчета Pascal.
Коэффициенты линейной функции
a1=-24.73516
a2=11.63471
Коэффициенты квадратичной функции
a1= 1.59678
a2=-0.62145
a3= 0.95543
Коэффициенты экспоненциальной функции
a1= 1.65885
a2= 0.40987
c= 0.50613
Xcp= 6.52320
Ycp=51.16040
Коэффициент корреляции 0.96196
Коэффициент детерминированности (линейная аппроксимация) 0.92537
Коэффициент детерминированности (квадратическая аппроксимация) 0.99409
Коэффициент детерминированности (экспоненциальная аппроксимация) 0.02691
Заключение.
Сделаем заключение по результатам полученных данных:
1. Анализ результатов расчетов показывает, что квадратичная аппроксимация наилучшим образом описывает экспериментальные данные т.к. согласно таблице 8 коэффициент корреляции - 0,9620; Коэффициенты детерминированности линейной аппроксимации - 0,9253; квадратической аппроксимации – 0,994; экспоненциальной аппроксимация – 0,0269.
2. Сравнивая результаты, полученные при помощи функции ЛИНЕЙН видим что они полностью совпадают с вычислениями, проведенными выше. Это указывает на то, что вычисления верны.
3. Полученное при построении линии тренда значение коэффициента детерминированности для экспоненциальной зависимости не совпадает с истинным значением поскольку при вычислении коэффициента детерминированности используются не истинные значения y, а преобразованные значения ln(y) с дальнейшей линеаризацией.
4. Результаты полученные с помощью программы на языке PASCAL полностью совпадают со значениями приведенными выше. Это говорит о верности вычислений.
Список литературы.
Ахметов К.С. Windows 95 для всех. - М.:ТОО "КомпьютерПресс", 1995.
Вычислительная техника и программирование. Под ред. А.В. Петрова. М.: Высшая школа, 1991.
Гончаров A., Excel 97 в примерах. — СПб: Питер, 1997.
Левин А., Самоучитель работы на компьютере. - М.: Международное агентство А.Д.Т., 1996.
Информатика: Методические указания к курсовой работе. Санкт-Петербургский горный институт. Сост. Д.Е. Гусев, Г.Н. Журов. СПб, 1999
|
 Скачать 1.31 Mb.
Скачать 1.31 Mb.