Информатика 7 вариант. Вариант 7. Арифметические основы функционирования компьютеров Задание 1 291,43
 Скачать 113.37 Kb. Скачать 113.37 Kb.
|
|
В итоге получаем:
Результат сложения: 000000000001111010001 Получили число 0000000000011110.10001. В десятичном представлении это число имеет вид: Для перевода целой части необходимо умножить разряд числа на соответствующую ему степень разряда. 0000000000011110 = 215*0 + 214*0 + 213*0 + 212*0 + 211*0 + 210*0 + 29*0 + 28*0 + 27*0 + 26*0 + 25*0 + 24*1 + 23*1 + 22*1 + 21*1 + 20*0 = 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 16 + 8 + 4 + 2 + 0 = 30 Для перевода дробной части необходимо разделить разряд числа на соответствующую ему степень разряда. 10001 = 2-1*1 + 2-2*0 + 2-3*0 + 2-4*0 + 2-5*1 = 0.53125 В итоге получаем число 30.53125 Результат сложения (в десятичном представлении): 30.53125 Логические основы функционирования компьютеров Задание 1 Функция Y=f(X1, X2,X3) задана в виде формулы. Необходимо представить функцию в виде таблицы и найти СДНФ 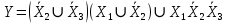 (⌐X2v⌐X3)*(X1v⌐X2)vX1*⌐X2*⌐X3
При решении были использованы таблицы истинности следующих операций. Операция ИЛИ — логическое сложение (дизъюнкция, объединение)
Операция И — логическое умножение (конъюнкция)
Операция НЕ — логическое отрицание (инверсия)
Совершенная конъюнктивная нормальная форма формулы (СКНФ) это равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций, удовлетворяющая свойствам: 1. Все элементарные дизъюнкции содержат все переменные, входящие в функцию F(x1,x2,...xn) 2. Все элементарные дизъюнкции различны 3. Каждая элементарная дизъюнкция содержит переменную один раз 4. Ни одна элементарная дизъюнкция не содержит переменную и её отрицание Задание 2 Функции трёх двоичных аргументов Y=f(X1, X2,X3) заданы в таблице. Необходимо представить функцию формулой СДНФ и минимизировать полученное выражение. Таблица истинности
Совершенная дизъюнктивная нормальная форма формулы (СДНФ) Минимизация булевой функций методом Квайна. Этап I. Операция попарного неполного склеивания. Сравниваем попарно все конъюнкции (минтермы 3-го ранга) и применяем там, где это возможно, правило склеивания.
Сравниваем попарно все конъюнкции (минтермы 2-го ранга) и применяем там, где это возможно, правило склеивания.
Этап II. Операция поглащения (покрытия). На втором этапе составляется импликантная таблица или таблица поглощений (перекрытий). Данная таблица позволяет упростить применение правила поглощения и одновременно отследить, все ли исходные конъюнкции (импликанты) учитываются в упрощенном выражении. В импликантную таблицу входят все исходные конъюнкции (в столбцах) и все конъюнкции, подвергшиеся склеиванию на последнем этапе (в строках), включая те, которые не склеились (если они имеются). В таблице на пересечении строки и столбца, к минтермам которых может быть применено правило поглощения, ставится отметка. После проставления всех отметок выбираются ядра (ядро) упрощенной функции. Ядро функции – это та сокращенная импликанта, которая единолично перекрывает какие-либо столбцы таблицы (т.е. в этих столбцах стоит только одна отметка). Упрощенная функция может иметь несколько ядер или не иметь их вообще. Если функция имеет ядро(а), то оно(и) должно(ы) обязательно присутствовать в минимальной формуле. Если функция не имеет ядра, то условно за ядро принимается та сокращенная импликанта, которая является наиболее простой и одновременно перекрывает как можно больше столбцов исходных импликант функции.
Ядро: Таким образом, получаем упрощенный методом Квайна вариант функции: f = ядро + дополнения Задание 3 Анализ автомата: требуется определить функцию, реализуемую автоматом в виде формулы: Представить функцию в виде таблицы; Упростить структуру автомата. Задание 4 Необходимо представить функцию в СДНФ и построить минимальный автомат на элементах И, ИЛИ, НЕ. x2*x3˅x1*⌐x3 Таблица истинности
Совершенная дизъюнктивная нормальная форма формулы (СДНФ) Минимизация булевой функций методом Квайна. Этап I. Операция попарного неполного склеивания. Сравниваем попарно все конъюнкции (минтермы 3-го ранга) и применяем там, где это возможно, правило склеивания.
Сравниваем попарно все конъюнкции (минтермы 2-го ранга) и применяем там, где это возможно, правило склеивания.
Этап II. Операция поглащения (покрытия). На втором этапе составляется импликантная таблица или таблица поглощений (перекрытий). Данная таблица позволяет упростить применение правила поглощения и одновременно отследить, все ли исходные конъюнкции (импликанты) учитываются в упрощенном выражении. В импликантную таблицу входят все исходные конъюнкции (в столбцах) и все конъюнкции, подвергшиеся склеиванию на последнем этапе (в строках), включая те, которые не склеились (если они имеются). В таблице на пересечении строки и столбца, к минтермам которых может быть применено правило поглощения, ставится отметка. После проставления всех отметок выбираются ядра (ядро) упрощенной функции. Ядро функции – это та сокращенная импликанта, которая единолично перекрывает какие-либо столбцы таблицы (т.е. в этих столбцах стоит только одна отметка). Упрощенная функция может иметь несколько ядер или не иметь их вообще. Если функция имеет ядро(а), то оно(и) должно(ы) обязательно присутствовать в минимальной формуле. Если функция не имеет ядра, то условно за ядро принимается та сокращенная импликанта, которая является наиболее простой и одновременно перекрывает как можно больше столбцов исходных импликант функции.
Ядро: Таким образом, получаем упрощенный методом Квайна вариант функции: f = ядро + дополнения |
