формулы. Арифметика и алгебра Пропорции
 Скачать 20.57 Kb. Скачать 20.57 Kb.
|
|
Арифметика и алгебра Пропорции В пропорции  числа a и d называются крайними членами, b и c – средними. Основное свойство пропорции: произведение крайних членов равно произведению средних, т.е. ad=bc, числа a и d называются крайними членами, b и c – средними. Основное свойство пропорции: произведение крайних членов равно произведению средних, т.е. ad=bc,Производные пропорции: 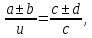  Действие со степенями (a  = =   ( ( = = , , , ,   , ( , ( Действия с корнями (корни предполагаются арифметическими, т.е. подкоренное выражение  0 и, кроме того, сам корень берется со знаком +). 0 и, кроме того, сам корень берется со знаком +).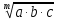 = =  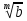  , ,  = =  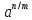 = =  , ,(  = =  = =  Прогрессии 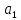 – первый член, – первый член,  – n-й член, d – разность арифметической прогрессии; – n-й член, d – разность арифметической прогрессии;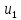 - первый член, - первый член,  – n-й член, q – знаменатель геометрической прогрессии; – n-й член, q – знаменатель геометрической прогрессии; – сумма n членов прогрессии, S – сумма бесконечно убывающей прогрессии: – сумма n членов прогрессии, S – сумма бесконечно убывающей прогрессии: = = 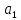 + d (n – 1), + d (n – 1),  = =  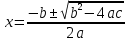    Логарифмы  Запись loga N = x равносильна записи ax = N, поэтому a logaN = N. Логарифмирование: logaa = 1, loga1 = 0. loga(MN) = logaM + logaN, loga 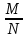 = logaM – logaN, = logaM – logaN,logaNm = mlogaN, loga  = =  aN aNобозначения: log10N = IgN, log0N = in N. соотношения: logba = 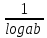 , logaN = , logaN =  (число logba в последней формуле называется модулем перехода от системы логарифмов с основанием b к системе с основанием а). Комбинаторика  pm = 1 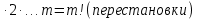  |
