Асиметричні криптосистеми. Асиметричні криптосистеми
 Скачать 159.09 Kb. Скачать 159.09 Kb.
|
|
АСИМЕТРИЧНІ КРИПТОСИСТЕМИ ЗМІСТ Словник термінів....................................................................................................4 Вступ........................................................................................................................8 Розділ 1. Загальний опис криптосистеми з відкритим ключем..........................9 Розділ 2. Порівняння симетричних та асиметричних криптосистем...............10 Розділ 3. Система шифрування RSA...................................................................11 Розділ 4. Питання про ідеальну криптосистему.................................................13 Розділ 5. Нематематичні методи зламу асиметричних шифрів........................14 Розділ 6. Математичні методи криптоаналізу RSA............................................16 Розділ 7. Передача секретних даних всередині ключа......................................19 Розділ 8. Використання асиметричних криптосистем для електронного підпису...................................................................................................................22 Висновки................................................................................................................24 Список використаних джерел..............................................................................25 СЛОВНИК ТЕРМІНІВ Розберемо поняття, що будуть зустрічатись в роботі найчастіше. Поліноміальний алгоритм – алгоритм, час виконання якого обмежений поліномом від довжини вхідного слова. Час роботи такого алгоритма обмежений 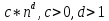 , де n – це довжина слова, d і c – деякі коефіцієнти. Як правило, алгоритми, що працюють з шифрами і ключами є поліноміальними. , де n – це довжина слова, d і c – деякі коефіцієнти. Як правило, алгоритми, що працюють з шифрами і ключами є поліноміальними.Функція Ейлера – це функція натурального аргументу m, яка дорівнює кількості натуральних чисел, що є взаємно простими з m і не перевищують його. Позначається 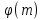 . У функції Ейлера є кілька дуже важливих властивостей: . У функції Ейлера є кілька дуже важливих властивостей:
Одним із основних понять асиметричного шифрування є поняття односторонньої функції. Одностороння функція – це функція, значення якої легко знайти для заданого аргументу, але аргумент складно знайти при заданому значенні функції. Такі функції мають наступні властивості:
Остання властивість строго не доведена для жодної функції, але поки що людству потрібні дуже великі обчислювальні потужності для інвертування деяких функцій. Серед односторонніх функцій також виділяють односторонні функції з секретом. Тут 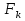 (x) – це сімейство односторонніх функцій, кожна з яких визначається секретом k. Їм притаманні наступні властивості: (x) – це сімейство односторонніх функцій, кожна з яких визначається секретом k. Їм притаманні наступні властивості:
Саме остання властивість надала такій функції назву функції-пастки, бо не знаючи секрету функції, неможливо її інвертувати. Важливим визначенням в системі шифрування є кільце залишків за модулем n. Кільце – це множина, на якій визначені операції додавання і множення, а поле – це множина, на якій визначені операції додавання, віднімання, множення та ділення. Опишемо ці поняття. Нехай на множині М визначений закон, за яким кожній парі елементів a, b із M однозначно ставиться у відповідність деякий елемент c є M. Тоді кажуть, що на М задана операція. Наприклад, на множині R дійсних чисел задані операції додавання і множення, яким притаманні наступні властивості:
(a + b) + c = a + (b + c) ;
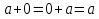 ; ;
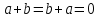 (елемент b називають протилежним до а); (елемент b називають протилежним до а);4) для довільних а, b є R 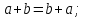 5) для довільних а, b, с є R a · (b · c) = (a · b) · c; 6) існує такий елемент 1 є R (не рівний 0), що для будь-якого а є R а · 1 = 1 · а = а; 7) для кожного а є R, а ≠ 0, існує такий елемент b є R, що а · b = b · a = 1 (елемент b називається оберненим до елемента а) ; 8) для довільних а, b є R а · b = b · a; 9) для довільних трьох елементів a, b, с є R a · (b + c) = a · b + a · c. Властивості 1) – 4) - властивості операції додавання, властивості 5) – 8) – властивості операції множення, а властивість 9) встановлює зв’язок між цими операціями. Множина F з двома визначеними на ній операціями множення та віднімання називається кільцем, якщо операції мають властивості 1)-5), 9). Приклад такої множини – множина цілих чисел. Якщо ж операціям додавання і віднімання притаманні властивості 1)-9), то F називається полем (прикладом поля є множина дійсних чисел). Особливо важливими для криптографії є скінченні поля. Сконструюємо одне із них. Нехай n – деяке натуральне число. Розіб’ємо множину цілих чисел Z на класи 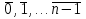 , де , де 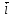 = {z є Z : z ≡ i (mod n)}. Неважко помітити, що два такі різні класи не перетинаються і Z = = {z є Z : z ≡ i (mod n)}. Неважко помітити, що два такі різні класи не перетинаються і Z = 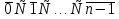 . .На множині Z : = { 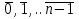 } визначимо операції додавання та множення наступним чином: } визначимо операції додавання та множення наступним чином: 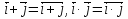 . Множина . Множина 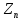 з так заданими операціями є кільцем, яке називається кільцем лишків за модулем n. Отже, кільце лишків за модулем n – це множина всіх можливих лишків, які можна отримати діленням натурального числа на n. з так заданими операціями є кільцем, яке називається кільцем лишків за модулем n. Отже, кільце лишків за модулем n – це множина всіх можливих лишків, які можна отримати діленням натурального числа на n.Позначимо символом 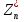 множину усіх тих класів , для яких існує обернений. множину усіх тих класів , для яких існує обернений. 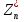 = = 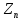 \ { \ {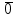 }, при чому }, при чому 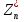 – поле. – поле. 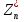 називають мультиплікативною групою кільця називають мультиплікативною групою кільця 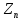 . Отже, мультиплікативна група – це множина чисел, взаємно простих за модулем n. . Отже, мультиплікативна група – це множина чисел, взаємно простих за модулем n.Спробуємо знайти елемент, обернений до 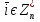 , тобто такий клас x, що , тобто такий клас x, що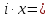 1, або, що те ж саме, знайдемо цілі числа x, y такі, що 1, або, що те ж саме, знайдемо цілі числа x, y такі, що 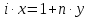 (звідси, (звідси, 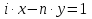 ). Останнє співвідношення означає, що ). Останнє співвідношення означає, що 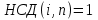 і із алгоритму Евкліда для цілих і та n необхідні числа x та y існують. і із алгоритму Евкліда для цілих і та n необхідні числа x та y існують.І навпаки, якщо НСД (і, n) = 1, то із алгоритма Евкліда 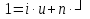 для деяких u та ʋ і матимемо: для деяких u та ʋ і матимемо: 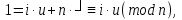 тобто тобто 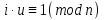 . .Також в роботі буде використано поняття хеш-функції. Хеш-функція – це математична функція, яка будь-якому масиву даних ставить у відповідність рядок фіксованої довжини, який ще називають хеш-сумою. Хеш-функції розробляють так, щоб незначні зміни вхідних даних викликали б значну зміну хеш-суми. З хеш-суми можна частково, але не повністю відтворити дані. ВСТУП З давніх часів людям необхідно було передавати інформацію по закритому каналу, тобто так, щоб ніхто інший її не знав. Для цього використовувались симетричні шифри, або шифри з закритим ключем. Це дозволяло створити захищений канал, але лише при наявності фізично захищеного каналу, наприклад, при приватній зустрічі. У 1974 році Ральф Меркле запропонував ідею шифрування з відкритим ключем. В основі цієї ідеї була можливість використання різних ключів для зашифрування і розшифрування даних. Запропонований їм алгоритм дозволяв домогтись того, що особам, що знали ключ, був потрібний час розшифровки N, а тим, що не знали – 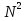 . Проте ідея не була достатньо розроблена для практичного використання. . Проте ідея не була достатньо розроблена для практичного використання.В 1976 році було опубліковано роботу «Нові напрямки в сучасній криптографії», авторами були Уітфілд Діффі і Мартін Хелман. Перебуваючи під впливом роботи Ральфа Меркле про поширення відкритого ключа, вони запропонували метод отримання однакових для двох користувачів секретних ключів, використовуючи відкритий канал. Цей методом неможливо було передати інформацію з пункту А до пункту Б, але він дозволяв отримати захищений канал без наявності фізично захищеного каналу. У 1977 році вчені Рональд Ривест, Аді Шамір і Леонард Адлеман з Масачусетського технологічного інституту розробили алгоритм шифрування, заснований на проблемі про розкладанні числа на множники. Система була названа за першими літерами їхніх прізвищ (RSA - Rivest, Shamir, Adleman). З’ясувалось, що система була винайдена ще в 1973 році Кліфордом Коксом, але не покинула межі центра урядового зв’язку Великобританії. RSA став першим алгоритмом, придатним і для шифрування, і для цифрового підпису. РОЗДІЛ 1 ЗАГАЛЬНИЙ ОПИС КРИПТОСИСТЕМИ З ВІДКРИТИМ КЛЮЧЕМ Користувач А, який хоче отримати зашифроване повідомлення, повинен вибрати деяку функцію 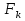 і надіслати опис цієї функції всім зацікавленим. Опис функції є відкритим ключем. При цьому секрет К він тримає у себе, він називається секретним або закритим ключем. і надіслати опис цієї функції всім зацікавленим. Опис функції є відкритим ключем. При цьому секрет К він тримає у себе, він називається секретним або закритим ключем.Користувач В, який хоче надіслати повідомлення, зашифровує свої дані Х і надсилає користувачу А інформацію 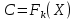 . Оскільки функція одностороння з секретом, то будь-який користувач, що перехоплює повідомлення С, не зможе його інвертувати. Лише користувач А, знаючи К, вміє інвертувати . Оскільки функція одностороння з секретом, то будь-який користувач, що перехоплює повідомлення С, не зможе його інвертувати. Лише користувач А, знаючи К, вміє інвертувати 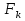 і за поліноміальний час отримує і за поліноміальний час отримує 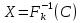 . .Отже, система шифрування з відкритим ключем включає в себе: А) Алфавіт А, в якому записують повідомлення; Б) Алфавіт Б, в якому записують крисптотексти; В) Має алгоритм генерування К; Г) Поліноміальний алгоритм створення функції 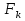 ; ;Д) Поліноміальний алгоритм створення оберненої функції. РОЗДІЛ 2 ПОРІВНЯННЯ СИМЕТРИЧНИХ ТА АСИМЕТРИЧНИХ КРИПТОСИСТЕМ
РОЗДІЛ 3 СИСТЕМА ШИФРУВАННЯ RSA Система шифрування використовує функцію піднесення в степінь по модулю в якості односторонньої. Спочатку генератор ключів випадковим чином генерує число n та два обернені в мультиплікативній групі 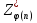 числа e та d. числа e та d.За класичною теоремою Ейлера: 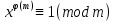 , де x і m – взаємно прості числа. , де x і m – взаємно прості числа.Згідно розгорнутому алгоритму Евкліда, якщо 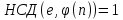 , то , то 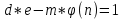 , де d і m – коефіцієнти, що розраховуються генератором. Тоді: , де d і m – коефіцієнти, що розраховуються генератором. Тоді: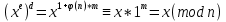 . .Тепер ми маємо задачу для генератора значень e і d: А) 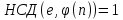 ; ;Б) 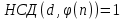 ; ;В) d – число, обернене до e в мультиплікативній групі 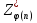 . Воно знаходиться методом Евкліда; . Воно знаходиться методом Евкліда;Г) Дізнатись 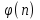 для деякого сгенерованого n. для деякого сгенерованого n.Останнє є найскладнішею задачею, що надає алгоритму RSA його властивостей. В загальному випадку 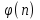 можна дізнатись лише шляхом перебору всіх значень від 1 до n – 1, що неможливо за поліноміальний час. Однак можна дізнатись можна дізнатись лише шляхом перебору всіх значень від 1 до n – 1, що неможливо за поліноміальний час. Однак можна дізнатись 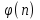 при створенні n, якщо генерувати n особливим шляхом. Роздивимось для цього властивості функції Ейлера. Можна помітити, що для простих чисел m і p: при створенні n, якщо генерувати n особливим шляхом. Роздивимось для цього властивості функції Ейлера. Можна помітити, що для простих чисел m і p:
Таким чином, можна одразу обчислити 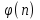 , якщо сгенерувати прості числа m і p, , якщо сгенерувати прості числа m і p, 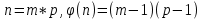 . .На практиці за числа m і p намагаються брати так звані сильні прості числа – прості числа, для яких число 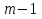 або або 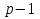 відповідно має великі множники. Це ускладнює задачу розкладу n на множники. відповідно має великі множники. Це ускладнює задачу розкладу n на множники.РОЗДІЛ 4 ПИТАННЯ ПРО ІДЕАЛЬНУ КРИПТОСИСТЕМУ Криптосистема з відкритим ключем вважається надійною при виконанні властивості д) односторонньої функції, яку вона використовує. Ідеальною вважалась би криптосистема, яка б містила в собі функцію, що мала б властивість е) не існує алгоритму знаходження x = 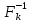 (y) при невідомому k. (y) при невідомому k.Але область визначення x є (0, 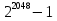 ) – це обмежена множина, в реальному житті вона обмежена апаратними можливостями і стандартами шифрування. Із цього і із властивості а) робимо висновок, що множина значень функції є множиною обмеженою. А тому існує алгоритм інвертування функції, навіть якщо він зводиться до банального перебору чисел. Таким чином, не існує абсолютно стійкого шифру на основі сьогоднішніх апаратних можливостей. ) – це обмежена множина, в реальному житті вона обмежена апаратними можливостями і стандартами шифрування. Із цього і із властивості а) робимо висновок, що множина значень функції є множиною обмеженою. А тому існує алгоритм інвертування функції, навіть якщо він зводиться до банального перебору чисел. Таким чином, не існує абсолютно стійкого шифру на основі сьогоднішніх апаратних можливостей.Незважаючи на те, що не існує ідеальних шифрів, шифр RSA на сьогоднішній день є достатньо надійним. Методи дешифрування залежать від особливостей криптосистеми і будуть розглянуті пізніше. РОЗДІЛ 5 НЕМАТЕМАТИЧНІ МЕТОДИ ЗЛАМУ АСИМЕТРИЧНИХ ШИФРІВ Існують методи, що дозволяють зламувати шифри не вдаючись до математики. Одною із схем є імітація адресата, або використання активного зловмисника. 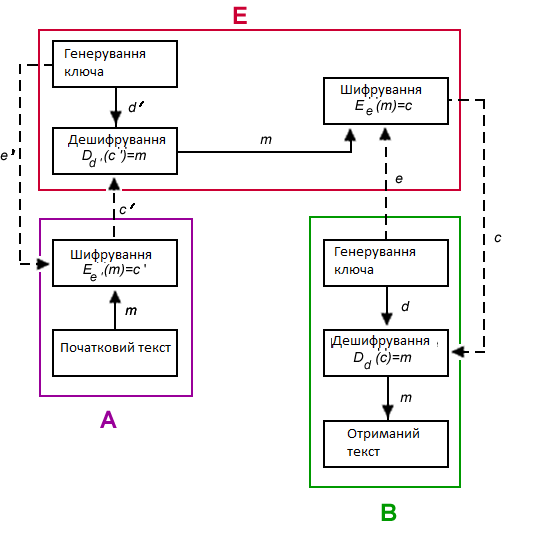 Ідея полягає у тому, що між пунктами A і B з’являеться активний зловмисник E. Коли B надсилає А відкритий ключ e, Е перехоплює його і генерує пару ключів 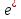 і і 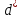 . Він надсилає А ключ . Він надсилає А ключ 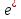 , А зашифровує повідомлення m і відправляє Е криптотекст , А зашифровує повідомлення m і відправляє Е криптотекст 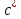 , думаючи, що Е – це В. Е розшифровує криптотекст , думаючи, що Е – це В. Е розшифровує криптотекст 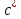 і отримує повідомлення m, яке при бажанні може змінити. Далі Е зашифровує m ключем d і відправляє В криптотекст c. В розшифровує c ключем d і отримує повідомлення m, вважаючи, що Е – це А. і отримує повідомлення m, яке при бажанні може змінити. Далі Е зашифровує m ключем d і відправляє В криптотекст c. В розшифровує c ключем d і отримує повідомлення m, вважаючи, що Е – це А.Найчастіше системою з відкритим ключем зашифровують ключі для системи з закритим ключем. Тож якщо m – це ключ для подальшого спілкування А і В за допомогою криптосистеми з закритим ключем, то Е може перейти в роль пасивного зловмисника і читати всю пошту А і В до тих пір, поки вони не змінять спільний ключ. Проблема в мережі Інтернет зазвичай вирішується введенням цифрового підпису, сертифікату, суспільновідомих розголошень ключів та третьої сторони, зазвичай Центра верифікації. Цими методами можна домогтись, щоб абонент А точно знав, що надіслане повідомлення від В не було пошкоджене ще кимось. Але при абсолютно відкритому каналі такого домогтись не вийде жодним чином. Втім, розглянуті випадки не впливають на надійність криптосистеми, яка продовжує бути надійної при нормальному каналі між А і В. Абсолютний захист від абонента Е в цій системі потребує розробки нового виду систем шифрування. РОЗДІЛ 6 МАТЕМАТИЧНІ МЕТОДИ КРИПТОАНАЛІЗУ RSA З самої появи криптосистеми RSA різні зловмисники намагалися розробити способи зламування цієї системи, натомість розробники намагались цим спробам запобігти. Як вже зазначалось, для дешифрування можна спробувати інвертувати односторонню функцію (Для RSA – це підведення в степінь по модулю). Програма для шифрування випадково сгенерувала n = 171327733 (24 біта у двійковому записі), e = 86746279, в якості повідомлення було вибрано m = 314159. Підхід був найпростіший: інвертування односторнньої функції. Програма – дешифратор перебирала всі можливі повідомлення, доки не знайшла правильного. Це зайняло в неї 44,37 с. Але є значно ефективніші алгоритми, пов’язані зі знаходженням закритого ключа. Для того, щоб його вирахувати, зловмиснику потрібні числа e і 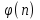 . На пошуку . На пошуку 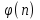 засновані всі математичні алгоритми зламування криптосистеми. засновані всі математичні алгоритми зламування криптосистеми.Перший спосіб його знаходження – за означенням 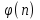 . На цей раз програма-дешифратор перевіряла всі числа до n, рахуючи кількість взаємно простих з ним, а потім генерувала ключі і розшифровувала шифр з відомим ключем. Програма впоралась за 1хв, 26,4с. Слід зауважити, що тут швидкість зламування не залежить від довжини повідомлення, а тільки від довжини ключа. . На цей раз програма-дешифратор перевіряла всі числа до n, рахуючи кількість взаємно простих з ним, а потім генерувала ключі і розшифровувала шифр з відомим ключем. Програма впоралась за 1хв, 26,4с. Слід зауважити, що тут швидкість зламування не залежить від довжини повідомлення, а тільки від довжини ключа.Але сам шифр RSA використовує напівпрості n, тому набагато логічніше було б знаходити 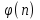 так само, як це робить генератор ключів. Для цього число n потрібно факторизувати, тобто розкласти на множники. Була створена програма, що перевіряла всі числа до n, чи були вони дільниками n. Алгоритм виявився значно ефективнішим і завершив роботу за 1,2мс. Складність цього алгоритму вважається так само, як це робить генератор ключів. Для цього число n потрібно факторизувати, тобто розкласти на множники. Була створена програма, що перевіряла всі числа до n, чи були вони дільниками n. Алгоритм виявився значно ефективнішим і завершив роботу за 1,2мс. Складність цього алгоритму вважається 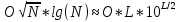 , де О – це коефіцієнт, умовна одиниця в розрахунку складності, а L – це довжина N. Звідси видно, що алгоритм не поліноміальний. , де О – це коефіцієнт, умовна одиниця в розрахунку складності, а L – це довжина N. Звідси видно, що алгоритм не поліноміальний.Проаналізуємо на основі цих даних стійкість криптосистеми RSA. Сгенероване n займало 24 біти, а реальний ключ RSA візьмемо для прикладу 1024 біти. Нехай 2/3 цього числа, тобто 682 біти займає число n, а інше – число e. Тоді рельний n на 28,5 порядків більше за згенерований. Порівняємо тепер складність алгоритмів і час їх виконання. 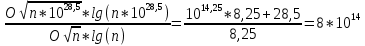 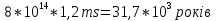 Слід зауважити, що складність алгоритму – це міра кількості операцій, потрібних для його виконання. Вона не бере в увагу складність виконання простих операцій. Але апаратні можливості не дозволяють процесору одночасно працювати з числами, більшими за 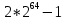 , тому великі числа доведеться розбивати на блоки в кращому випадку по 64 біти кожний. Це має збільшити час роботи алгоритму у , тому великі числа доведеться розбивати на блоки в кращому випадку по 64 біти кожний. Це має збільшити час роботи алгоритму у 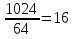 разів (до 507 тис.років). разів (до 507 тис.років).Але існують і інші методи факторизації, наприклад алгоритм Полларда. Це – вірогіднісний алгоритм, за яким генеруються числові значення, які з більшою вірогідністю є дільниками N, ніж числа при переборі всіх чисел. Саме тому в середньому N факторизується алгоритмом Полларда швидше. Складність алгоритму 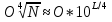 . Алгоритм також не є поліноміальним. . Алгоритм також не є поліноміальним.На сьогоднішній момент найкращим алгоритмом факторизації на звичайних компьютерах є алгоритм квадратичного решета з складністю 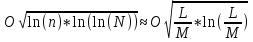 , де М = 0,4343 , де М = 0,4343Але існують більш ефективні спеціальні алгоритми зламу. Одним із них є атака Вінера. Алгоритм виконується за поліноміальний час, але дає результат лише у випадку, коли точно відомо, що 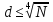 . Деякі програми можуть вдаватись до зменшення числа d для можливості швидшого розшифрування повідомлень, що дає зловмисникам більше шансів. Атака Вінера – один з небагатьох алгоритмів, що не намагається факторизувати N, натомість він шукає підходящий закритий ключ. Складність оцінюється як . Деякі програми можуть вдаватись до зменшення числа d для можливості швидшого розшифрування повідомлень, що дає зловмисникам більше шансів. Атака Вінера – один з небагатьох алгоритмів, що не намагається факторизувати N, натомість він шукає підходящий закритий ключ. Складність оцінюється як 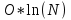 . .Також слід зазначити, що існує алгоритм Шора для факторизації числа N, який є поліноміальним і не має умов. Складність алгоритму оцінюється як 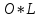 . Але виконуватись він повинен на поки що теоретичних квантових компьютерах, і поки що не йдеться про будь-які практичні застосування цього алгоритму. . Але виконуватись він повинен на поки що теоретичних квантових компьютерах, і поки що не йдеться про будь-які практичні застосування цього алгоритму.РОЗДІЛ 7 ПЕРЕДАЧА СЕКРЕТНИХ ДАНИХ ВСЕРЕДИНІ КЛЮЧА Можна побачити, що для математичного криптоаналізу чистого RSA потрібно достатньо багато часу, і такий метод зламу майже не використовується на практиці. Але є спосіб, як «зіпсувати» RSA, надати йому властивостей, що роблять злам можливим. Спосіб заключається в вмонтуванні секретної інформації в сам відкритий ключ. Ця інформація може містити деякі корисні інструкції для особи, що буде зламувати ключі, обмежити межі пошуку відкритого ключа, тощо. 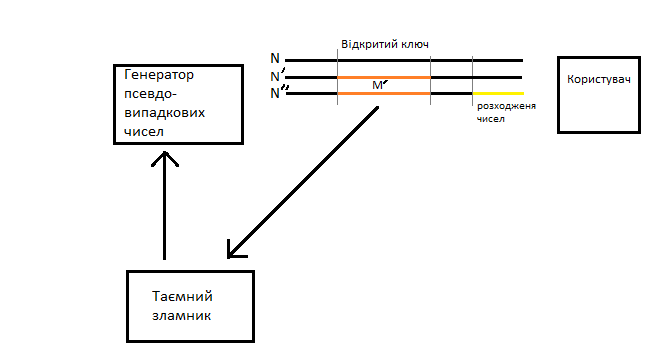 Алгоритм наступний: деякий таємний зламник генерує закритий і відкритий ключ для деякої асиметричної криптосистеми, не обов’язково RSA (Хоча можна використовувати і симетричну криптосистему, але тоді вмонтовану інформацію зможе бачити сам сервер). Він передає серверу, що отримує дані користувачів, деякі дані: зміщення секретних даних, розмір і свій відкритий ключ. Тепер припустимо, що користувач хоче передати серверу дані. Сервер генерує числа m, p, N і одразу просте d. Далі він бере деякі дані секретні дані M, наприклад m, d або їх хеш-функцію, які можуть бути використані для зламу і зашифровує їх ключем, що передав йому таємний зламник, отримує 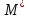 . Сервер заміщує деяку частину N на . Сервер заміщує деяку частину N на 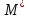 побітово, отримує побітово, отримує 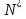 , генерує , генерує 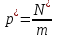 . Далі він шукає таке просте . Далі він шукає таке просте 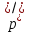 , яке стоїть найближче до , яке стоїть найближче до 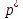 , генерує , генерує 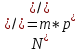 , яке і стає новим N. , яке і стає новим N. 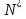 знаходиться відносно близько на числовій осі до знаходиться відносно близько на числовій осі до 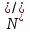 , але не дорівнює йому. Тому , але не дорівнює йому. Тому 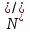 побітово дорівнює побітово дорівнює 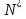 до деякого біта. Отже, потрібно таке зміщення і розмір даних до деякого біта. Отже, потрібно таке зміщення і розмір даних 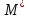 , щоб вони не спотворились в результаті переходу від , щоб вони не спотворились в результаті переходу від 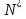 до до 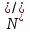 . .Далі генератор рахує 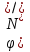 ). Оскільки d – наперед просте число, то воно буде взаємно простим з ). Оскільки d – наперед просте число, то воно буде взаємно простим з 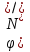 , таким чином необхідна умова буде виконана. Далі вираховується відкритий ключ e за алгоритмом Евкліда. , таким чином необхідна умова буде виконана. Далі вираховується відкритий ключ e за алгоритмом Евкліда.Тепер треба звернути увагу на те, що при всіх перетвореннях m ще є дійсним множником числа 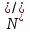 , а d – дійсним закритим ключем. Тепер сервер може відправити ключ (e, N) користувачу або використати його в якості відкритого ключа для верифікації підписів деякого користувача. , а d – дійсним закритим ключем. Тепер сервер може відправити ключ (e, N) користувачу або використати його в якості відкритого ключа для верифікації підписів деякого користувача.Таємний зламник, що знає закритий ключ, розмір і зміщення 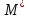 , може з будь-якого , може з будь-якого 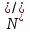 витягти корисні для нього дані М, а потім деяким чином зламати шифр або на багато порядків скоротити час підбору ключа до шифру. Таємний зламник при цьому займає роль пасивного зловмисника і не втручається в процес передачі даних. При цьому ніхто інший не зможе довести, що шифр був підроблений таким чином. витягти корисні для нього дані М, а потім деяким чином зламати шифр або на багато порядків скоротити час підбору ключа до шифру. Таємний зламник при цьому займає роль пасивного зловмисника і не втручається в процес передачі даних. При цьому ніхто інший не зможе довести, що шифр був підроблений таким чином.З точки зору будь-яких інших зловмисників число 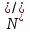 буде лише напівпростим псевдовипадковим числом. Вони не будуть знати, чи зіпсоване число N, чи ні, не будуть знати закритого ключа буде лише напівпростим псевдовипадковим числом. Вони не будуть знати, чи зіпсоване число N, чи ні, не будуть знати закритого ключа 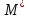 , його розміру, зміщення та криптосистеми, яким воно було зашифроване. Таким чином, якщо інший зловмисник захоче зламати RSA спираючись на те, що N зіпсоване, йому доведеться зламувати всі частини числа N всіма можливими алгоритмами зламу. Очевидно, що це є набагато складнішою задачею, ніж сам злам RSA. , його розміру, зміщення та криптосистеми, яким воно було зашифроване. Таким чином, якщо інший зловмисник захоче зламати RSA спираючись на те, що N зіпсоване, йому доведеться зламувати всі частини числа N всіма можливими алгоритмами зламу. Очевидно, що це є набагато складнішою задачею, ніж сам злам RSA.Сам злам RSA буде так само зводитись до факторизації N, алгоритм зламу не працює з підбором ключа, а тому той факт, що d просте число ніяк не допоможе зловмиснику. Таким чином ми маємо спосіб генерування ще одного закритого ключа для RSA і надійність криптосистеми при цьому не страждає. РОЗДІЛ 8 ВИКОРИСТАННЯ АСИМЕТРИЧНИХ КРИПТОСИСТЕМ ДЛЯ ЕЛЕКТРОННОГО ПІДПИСУ Електронний підпис - це вид криптографічних функцій, що дає змогу встановити походження файла і його належність певному користувачу. 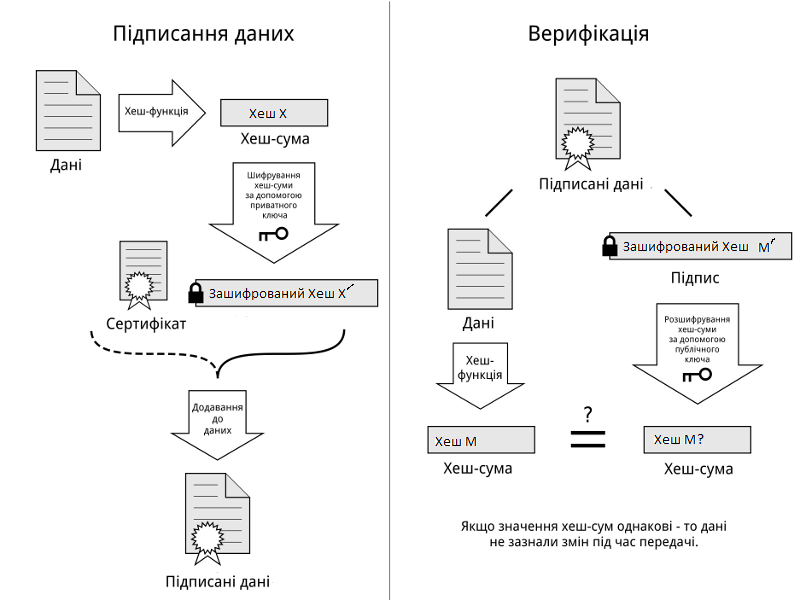 Схема електронного підпису по асиметричній схемі наступна: корисувач А генерує пару ключів: відкритий (e, n) і закритий (d, n). Відкритий ключ передається Центру верифікації і є загальнодоступним, закритий ключ зберігається у користувача і є аналогом реального підпису. Якщо користувач А хоче відправити підписаний файл, він знаходить його хеш-функцію Х і зашифровує її своїм закритим ключем (d, n), отримуючи зашифровану хеш-суму 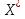 , яку він додає до самого файлу разом з сертифікатом. , яку він додає до самого файлу разом з сертифікатом.Якщо деякий корисувач В завантажив файл і хоче перевірити його похождення, він знаходить хеш-функцію з файлу, що отримав. Назвемо її М. Надіслану разом з файлом зашифровану хеш-суму назвемо 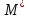 . Далі корисувач В завантажує відкритий ключ (e, n) і розшифровує ним . Далі корисувач В завантажує відкритий ключ (e, n) і розшифровує ним 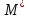 , отримуючи , отримуючи 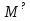 . У разі правильної передачі він отримує . У разі правильної передачі він отримує 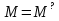 . .Нехай деякий зловмисник Е підмінив надісланий користувачем А файл на інший з хешем М. Оскільки він не знає ключа (d, n), то він не може зашифрувати М так, щоб користувач В при розшифровці ключем (e, d) отримав хеш М. Таким чином, намір зловмисника буде зірваний. В додаток до цього захисту, сам файл може являти собою зашифровані ключами користувача В дані, які користувач А хоче йому надіслати. При справному Центрі верифікації встановлений таким чином канал між А і В можна вважати захищеним. Окрім асиметричної схеми, існує симетрична схема електронного підпису. Замість закритого ключа там використовується повний ключ, замість відкритого – частина повного ключа. Ці схеми вважаються більш надійними, але використовуються рідше через великі розміри підписаних файлів і велике апаратне навантаження. ВИСНОВКИ В роботі розглянуто основні події, що сприяли формуванню криптосистеми з відкритим ключем. Сформульовано принципи побудови криптосистем з відкритим ключем, описані необхідні математичні поняття. Побудований загальний алгоритм криптосистеми з відкритим ключем. В якості прикладу було взято криптосистему RSA, розглянуті її математичні принципи та закономірності. В роботі описані алгоритми шифрування та генерування ключів. Написані декілька програм для шифрування, дешифрування та зламу шифру декількома способами. Розглянутий спосіб псування шифру RSA таким чином, щоб його можна було зламати ключем, відмінним від закритого. Розглянуті інші, нематематичні способи зламу. На основі даних про час виконання написаних програм проаналізовано стійкість криптосистеми RSA, порівняно симетричні та асиметричні криптосистеми. Окрім шифрування, було приділено увагу також алгоритму електронного підписання та верифікації даних. СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
|

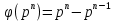 , де p – просте, n – натуральне;
, де p – просте, n – натуральне;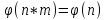 *
*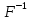 (y).
(y).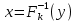 , яка кожному y ставить в відповідність x;
, яка кожному y ставить в відповідність x;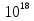 років
років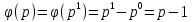 , про що насправді не важко здогадатись за означенням функції Ейлера;
, про що насправді не важко здогадатись за означенням функції Ейлера;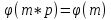 *
* 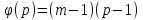 .
.