Атаки на эллиптические кривые

• Название: Атаки на эллиптические кривые
• Дата: 06.03.2022
• Размер: 191.67 Kb.
• Имя файла: Referat (1).docx
• Тип: Реферат; #384804
• страница: 5 из 19

Эллиптическая криптография

Самый явный путь решения проблемы повышения стойкости - представление шифруемых блоков информации в криптографических алгоритмах не только с помощью чисел, но и с помощью иных алгебраических элементов большей сложности. Самыми подходящим типами таких элементов являются точки эллиптических кривых.
Эллиптические кривые считаются одними из наиболее перспективных объектов для изучения в современной теории чисел и криптографии. Так, например, на эллиптических кривых основан российский стандарт электронно- цифровой подписи ГОСТ Р 34.10-2001.[6]

3. Математика эллиптической кривой и конечных полей

Эллиптической кривой E называют множество пар точек (x, y), удовлетворяющих уравнению (1.1):

𝑦² + 𝑎₁𝑥𝑦 + 𝑎₃𝑦 = 𝑥³ + 𝑎₂𝑥² + 𝑎₄𝑥 + 𝑎₆ (1.1) Варианты графиков эллиптических кривых приведены на рисунке 1.1.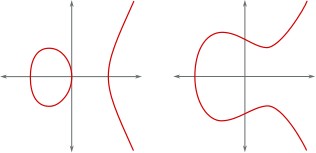



Рис. 1.1 – Графики эллиптических кривых
В большинстве случаев в криптографии основанных на эллиптических кривых рассматриваются 2 вида кривых над конечными полями:

1. 
   простыми полями нечётной характеристики (Zp, где p> 3 и является простым числом)
   
2. 
   полями характеристики 2 (GF(2^m)).
   

В полях характеристики 2 обычно рассматриваются два вида эллиптических кривых (1.2) и (1.3):

1. 
   Суперсингулярная кривая
   

𝑦² + 𝑎𝑦 = 𝑥³ + 𝑏𝑥 + 𝑐 (1.2)

2. 
   Несуперсингулярная кривая
   

𝑦² + 𝑎𝑥𝑦 = 𝑥³ + 𝑏𝑥² + 𝑐 (1.3)

Но далеко не все эллиптические кривые подходят для реализации в эллиптической криптографии.
Согласно ГОСТ 24.10-2012, эллиптическая кривая E(Fp) над конечным простым полем Fp, где p – является порядком поля, которое должно быть больше 3, может быть отображена с помощью модифицированного уравнения, также называемым «каноническим», в форме Вейерштрасса, которая вычисляется по формуле (1.4):

𝑦² = 𝑥³ + 𝑎𝑥 + 𝑏 (𝑚𝑜𝑑 𝑝) (1.4)
где a и b принадлежат полю Fp и дискриминант 4𝑎³ + 27𝑏² не должен равняться 0 по модулю p. Если это неравенство не может быть выполнено, то кривые считаются сингулярными. В математике сингулярностью обозначается такая точка, в которой предложенная функция имеет странное поведение, например, стремится к бесконечности. Ученые считают, что использование сингулярных кривых в алгоритмах криптографии приводят к уменьшению криптостойкости алгоритма. Поэтому использование таких кривых запрещено.

Все арифметические вычисления в эллиптической криптографии проходят не над выбранной кривой, а только над точками, которые принадлежат этой кривой, которые в свою очередь образуют определенную группу. Над точками кривой могут быть выполнены следующие три основные операции:

1. 
   сложение двух разных точек
   
2. 
   удвоение точки
   
3. 
   умножение точки на число
   

Основной операцией является операция сложения, так как именно на ней основываются все дальнейшие операции.

1. 
   Сложение точек на эллиптической кривой
   

Сложение двух точек эллиптической кривой заключается в том, что если взять две точки P и Q, которые лежат на данной кривой, и провести через них прямую, то эллиптическая кривая будет иметь пересечение этой прямой в
третьей точке. Так как эллиптическая кривая будет симметричной относительно оси Х, то мы можем зеркально отразить эту точку относительно оси X, получив новую точку P+Q принадлежащую данной кривой (Рис. 1.2).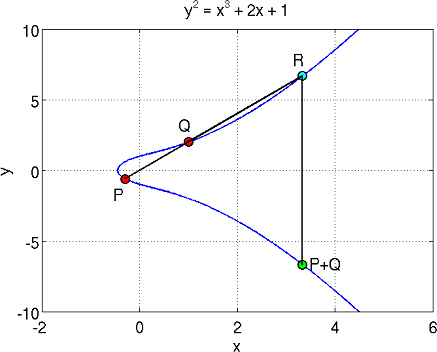



Рис. 1.2 – Сложение точек на эллиптической кривой
Пусть дана кривая
𝑦² = 𝑥³ + 𝑎𝑥 + 𝑏 (1.5)
над полем k (𝑘 ≠ 2 и 𝑘 ≠ 3), и точки P=(𝑥_𝑝, 𝑦_𝑝) и Q=(𝑥_𝑞, 𝑥_𝑞) принадлежащие кривой (1.5)

Предположим, что 𝑥_𝑝 ≠ 𝑥_𝑞.
Пусть формула нахождения углового коэффициент секущей

_{𝑆 =} 𝑦_𝑝−𝑦_𝑞

𝑥_𝑝−𝑥_𝑞

(𝑚𝑜𝑑 𝑘) (1.6)

так как k — поле, то s строго определено.
Тогда мы можем определить 𝑅 = 𝑃 + 𝑄 = (𝑥_𝑟, 𝑦_𝑟) следующим образом:
𝑥_𝑟 = 𝑠² − 𝑥_𝑝 − 𝑥_𝑞 (𝑚𝑜𝑑 𝑘) (1.7)

𝑦_𝑟 = 𝑠⁽𝑥_𝑃 − 𝑥_𝑅⁾ − 𝑦_𝑝 (𝑚𝑜𝑑 𝑘) (1.8)
Формулы сложения (1.7) и (1.8) показывают, что координаты суммы двух точек выражаются через координаты слагаемых рационально, следовательно, если координаты выбранных точек принадлежат выбранному полю, то и сумма этих точек принадлежит этому же полю. [8]

2. 
   Удвоение точек на эллиптической кривой
   

Удвоение точки эллиптической кривой происходит немного по-другому, нежели сложение двух точек. Основное отличие заключается в нахождении углового коэффициент секущей, проведенной через точку.

Он высчитывается по формуле (1.9)

_{𝑆 =} 3𝑥_𝑝+𝑎

2𝑦_𝑝

(𝑚𝑜𝑑 𝑘) (1.9)

Вычисление же координат остается неизменным, они вычисляются по формулам (1.7) и (1.8).

3. 
   Оценка числа элементов группы точек эллиптической кривой
   

Данные свойства позволяет говорить о конечной группе точек в котором можно строить криптографические алгоритмы.

Для выбранной эллиптической кривой количество точек в группе конечно. Данное количество точек в группе эллиптической кривой m можно определить по формуле (1.10):

𝑝 + 1 − 2_√𝑝 ≤ 𝑚 ≤ 𝑝 + 1 + 2_√𝑝 (1.10) где р – порядок поля, над которым определена кривая.