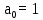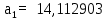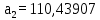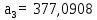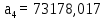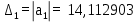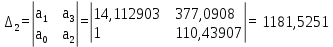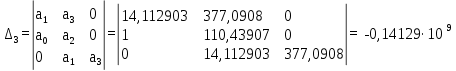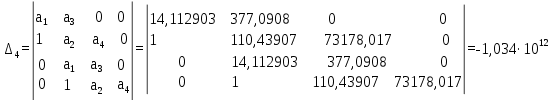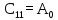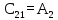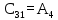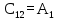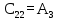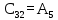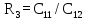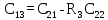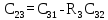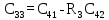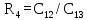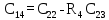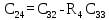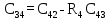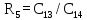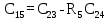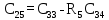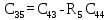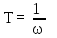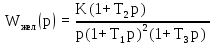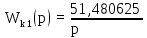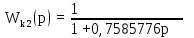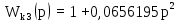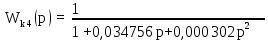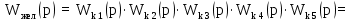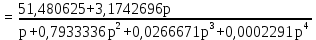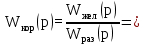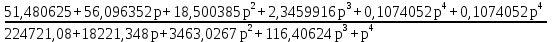Курсовой ТАУ. Автоматического управления, система автоматического регулирования, передаточные функции, устойчивость системы, коррекция системы
 Скачать 2.38 Mb. Скачать 2.38 Mb.
|
 Аннотация Курсовой проект объем работы с 32, 29 рис , 4 табл , 7 источников. ГЕНЕРАТОР, ДВИГАТЕЛЬ ПОСТОЯННОГО ТОКА, АМПЛИТУДО-ЧАСТОТНАЯ ХАРАКТЕРИСТИКА, СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ, СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ, ПЕРЕДАТОЧНЫЕ ФУНКЦИИ, УСТОЙЧИВОСТЬ СИСТЕМЫ, КОРРЕКЦИЯ СИСТЕМЫ Объектом исследования являются принципиальная схема САУ электродвигателя постоянного тока Цель работы: рассчитать статическую систему стабилизации скорости электродвигателя постоянного тока Результатом исследования является получение системы стабилизации скорости вращения электродвигателя постоянного тока с необходимыми параметрами По полученным в результате расчета параметрам можно собрать систему стабилизации скорости вращения электродвигателя постоянного тока с максимально приближенными к расчетным характеристикам Система будет обладать заданной степенью колебательности, заданными запасом по модулю и по фазе и наименьшей возможной статической ошибкой Первым этапом расчетной части работы является составление дифференциальных уравнений и передаточных функций, входящих в систему звеньев Вторым этапом является проверка системы на устойчивость по 4 критериям Третьим этапом является коррекция системы Четвертым этапом является моделирование полученной системы с учетом корректирующего устройства Содержание
Нормативные ссылки В курсовом проекте использованы ссылки на следующие стандарты (нормативные документы): ГОСТ 2.102 – 2013 ЕСКД. Виды и комплектность конструкторских документов; ГОСТ 2.104 - 2006 ЕСКД. Основные надписи; ГОСТ 2.105 - 2011 ЕСКД. Общие требования к текстовым документам; ГОСТ 2.106 – 2005 ЕСКД. Текстовые документы; ГОСТ 2.109 – 2007 ЕСКД. Основные требования к чертежам; ГОСТ 2.111 – 2013 ЕСКД. Нормоконтроль; ГОСТ 2316 – 2008 ЕСКД. Правила нанесения на чертежах надписей, технических требований и таблиц. Сокращения и обозначения САУ – система автоматического управления; САР - системы автоматического регулирования; ОУ – обмотка управления; ОВД – обмотка возбуждения двигателя; К1 - коэффициент усиления промежуточного усилителя ПУ; К2, К3, К4, К5 - коэффициенты передачи других звеньев систем; ТY, TK, TЭ-постоянные времени электромашинного усилителя; Тя, Тм - постоянные времени двигателя; Iя,Ω - ток якоря и скорость двигателя; Мд, Мс - электромагнитный момент двигателя и момент статический (сопротивления движению); е = U3-Uос - сигнал ошибки (отклонение) в системах. U3- задающее напряжение; Uос- напряжение обратной связи; Uy- напряжение усилителя; ПУ - промежуточный усилитель; Д - двигатель; ЭМУ - электромашинный усилитель Введение Теория автоматического управления (ТАУ) — научная дисциплина, предметом изучения которой являются информационные процессы, протекающие в автоматических системах управления. ТАУ выявляет общие закономерности функционирования, присущие автоматическим системам различной физической природы, и на основе этих закономерностей разрабатывает принципы построения высококачественных систем управления. При изучении процессов управления в ТАУ абстрагируются от физических и конструктивных особенностей систем и вместо реальных систем рассматривают их адекватные математические модели, поэтому основным методом исследования в ТАУ является математическое моделирование. Кроме того, методологическую основу ТАУ образуют теория обыкновенных дифференциальных уравнений, операционное исчисление (преобразование Лапласа), гармонический анализ (преобразование Фурье). ТАУ вместе с теорией функционирования элементов систем управления (датчиков, регуляторов, исполнительных механизмов) образует более широкую отрасль науки — автоматику. Автоматика в свою очередь является одним из разделов технической кибернетики. Первые теоретические работы в области автоматического управления появились в конце XIX в., когда в промышленности получили широкое распространение регуляторы паровых машин, и инженеры-практики стали сталкиваться с трудностями при проектировании и наладке этих регуляторов. Именно в этот период крупный русский ученый и инженер И.А. Вышнеградский выполнил ряд научных исследований, в которых впервые паровая машина и ее регулятор были проанализированы математическими методами как единая динамическая система. В дальнейшем выдающиеся русские ученые А.М. Ляпунов и Н.Е. Жуковский создали основы математической теории процессов, протекающих в автоматически управляемых машинах и механизмах. Задание на курсовой проект 1 Задание на курсовой проект Исходными данными при выполнении курсового проекта являются принципиальная схема статической системы стабилизации скорости электродвигателя постоянного тока в исходном варианте (без коррекции), параметры неизменяемой части и технические требования, которым должна удовлетворять спроектированная система К техническим требованиям при выполнении курсовой работы относятся показатели качества, основными из которых являются время регулирования и максимальное перерегулирование при отработке управляющих воздействий На рис изображена принципиальная схема САУ 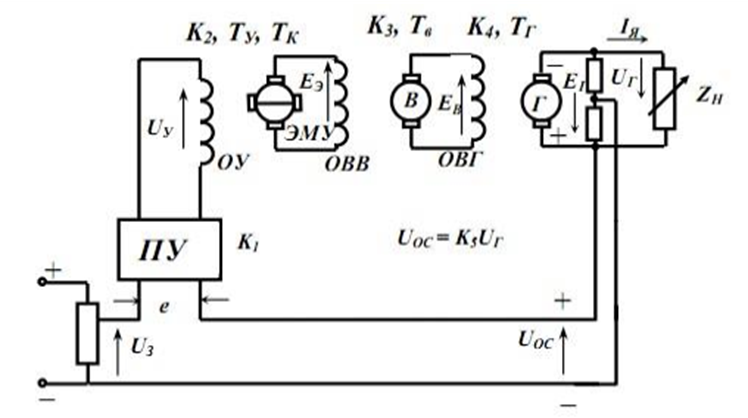 Рисунок 1.1 – Принципиальная схема САУ В таблице 1.1 представлены исходные данные для САУ. В таблице 1.2 представлены требования задания курсового проекта. Таблица 1.1 – Данные элементов системы автоматического регулирования
Таблица 1.2 – Требования задания курсового проекта
Для выполнения работы необходимо: 1. Дать краткое описание работы САУ. 2. Разбить систему на элементы (звенья) и составить передаточные функции для каждого звена. 3. Построить структурную схему САУ. 4. Вывести выражения для передаточных функций системы в разомкнутом и замкнутом состояниях по управляющему и возмущающему воздействиям. 5. Проверить исходную систему на устойчивость по критериям. 6. Рассчитать параметры корректирующего звена. 7. Смоделировать скорректированную систему. 2 Краткое описание принципа действия системы С помощью потенциометра на входе системы задаем напряжение U3, которое в начальный момент времени подается на ОВВ. Основным способом возбуждения синхронных машин является электромагнитное возбуждение. Для питания обмотки возбуждения Г в данной схеме применяется специальный генератор постоянного тока, называемый возбудителем В, обмотка возбуждения которого ОВВ получает питание постоянного тока от другого звена ЭМУ. При прохождении по обмотке ОВГ постоянного тока возникает ЭДС возбуждения, которая наводит в магнитной системе машины магнитное поле. Генератор вырабатывает напряжение Uг. На выходе системы стоит делитель напряжения. Часть напряжения Uг, снятое с делителя напряжения по каналу ОС, поступает на вход ПУ, поступает уже ошибка «е», которая автоматически меняется при изменении Uг. Если Uг повысилось, то «е» уменьшается и, следовательно, уменьшается ток в ОВГ и напряжение Uг уменьшается до нужной величины. Обратный процесс происходит при уменьшении Uг. Таким образом происходит автоматическое регулирование. 3 Разбиение системы на элементы 1) ПУ − промежуточный усилитель. Предназначен для усиления мощности сигнала задающего генератора и получения кривой переменного тока прямоугольной формы. Передаточная функция ПУ:
Промежуточный усилитель является пропорциональным звеном. 2) ЭМУ – электромашинный усилитель, предназначенный для усиления мощности подаваемого на обмотку возбуждения сигнала за счет механической энергии первичного двигателя. ЭМУ используется для того, чтобы сигналом малой мощности контролировать сигнал большой мощности. Передаточная функция ЭМУ:
ЭМУ является апериодическим звеном 1-го порядка 3) В – возбуждение генератора – создает рабочее магнитное поле, благодаря которому в вращающемся якоре создается ЭДС:
Двигатель является апериодическим звеном 2-го порядка 4) Генератор-объект регулирования устройства, преобразующий механическую энергию, получаемую от двигателя в электрическую.
Генератор является апериодическим звеном 1-го порядка 5) ОС-обратная связь
Обратная связь является пропорциональным звеном. 4 Построение структурной схемы САУ Структурная схема системы автоматического регулирования строится на основе функциональной схемы, которая для данной системы стабилизации скорости вращения вала состоит из последовательно соединенных ПУ, ЭМУ, генератора, двигателя и тахогенератора. Последнее устройство выполняет функции обратной связи. На рисунке 4.1. изображена структурная схема для данной САУ.  Рисунок 4.1 - Структурная схема САУ Для данной схемы:
На рисунке 4.2 представлен программный код, реализованный в среде Scilab. Он предназначен для расчета передаточных функций звеньев. 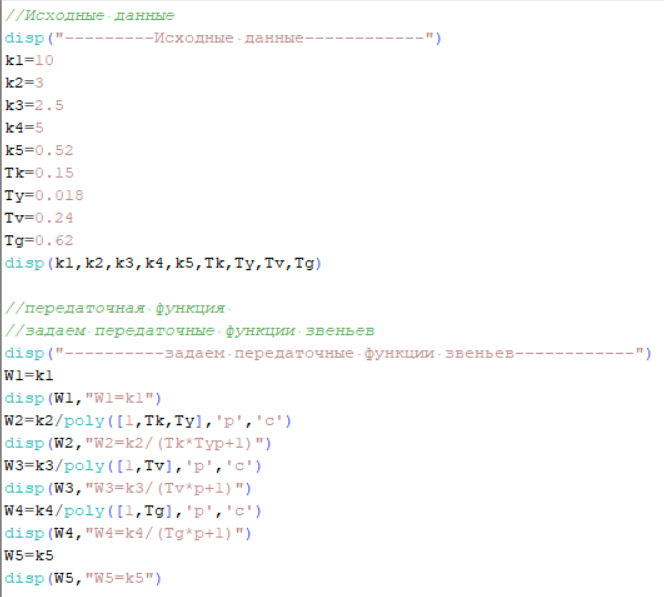 Рисунок 4.2 – Программный код, реализованный в среде Scilab 5 Передаточные функции системы Передаточная функция разомкнутой системы находится как произведение передаточных функций пяти последовательно соединённых инерционных звеньев, описанных в предыдущем разделе:
Передаточная функция цепи обратной связи по задающему воздействию:
Передаточная функция замкнутой системы:
На рисунке 5.1 представлен программный код, реализованный в среде Scilab. Он предназначен для расчета передаточных функций системы. 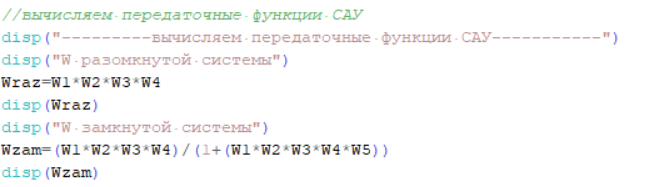 Рисунок 5.1 – Программный код для вычисления передаточных функций САУ 6 Проверка системы на устойчивость Чтобы проверить систему на устойчивость, найдем корни характеристического уравнения. Если все корни характеристического уравнения отрицательны, то система устойчива. Характеристическое уравнение для разомкнутой системы:
Корни характеристического уравнения (6.1): -4,1666667 + 6,1801654i -4,1666667 – 6,1801654i -4,1666667 -1,6129032 Все корни отрицательны, следовательно, система устойчива. Характеристическое уравнение для замкнутой системы:
Корни характеристического уравнения (6.2): -14,750166 + 12,03907i -14,750166 – 12,03907i 7,6937143 + 11,9446i 7,6937143 – 11,9446i Не все корни отрицательны, следовательно, система не устойчива. На рисунке 6.1 представлен программный код, предназначенный для решения характеристических уравнений.  Рисунок 6.1 – Программный код, предназначенный для решения характеристических уравнений Построим переходную характеристику системы. Она изображена на рисунке 6.2. На рисунке 6.3 представлен необходимый для этого программный код. 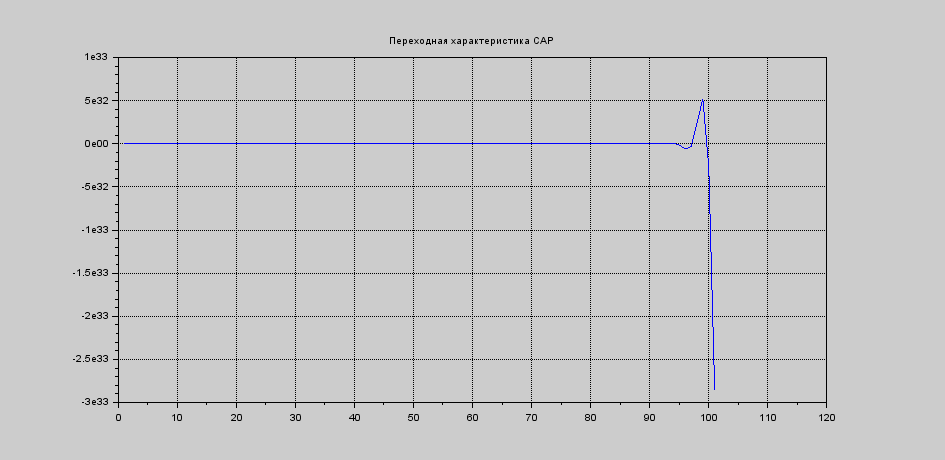 Рисунок 6.2 - Переходная характеристика системы  Рисунок 6.3 – Программный код для построения переходной характеристики Для более точной проверки системы на устойчивость, воспользуемся критериями устойчивости. 6.1 Критерий Найквиста Исследование системы на устойчивость по критерию Найквиста производится путем построения амплитудно-фазовой характеристики разомкнутой системы. Для того чтобы система была устойчива, необходимо и достаточно чтобы график не охватывал точку (−1; 0) на комплексной плоскости. Построим годограф Найквиста (рис. 6.4). Отметим проекции точки (-1;0) на оси для того, чтобы увидеть, выполняется условие или нет. На рисунке 6.5 представлен необходимый для построения АФХ код. 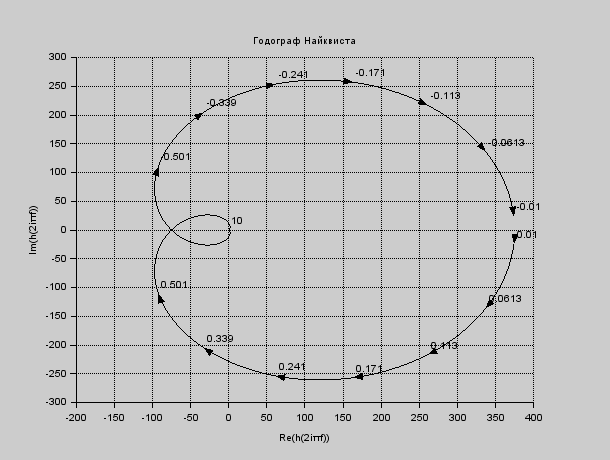 Рисунок 6.4 – Годограф Найквиста Система является устойчивой, т.к. данный график не пересекает точку (-1;0).  Рисунок 6.5 – Программный код для построения годографа Найквиста 6.2 Критерий Михайлова Для устойчивости линейной системы необходимо и достаточно, чтобы годограф Михайлова при изменении частоты от 0 до ω начинался на вещественной оси, и проходил последовательно против часовой стрелки 4 квадрантов комплексной плоскости. На рисунке 6.6 представлен годограф Михайлова, на рисунке 6.7 – необходимый для его построения программный код. 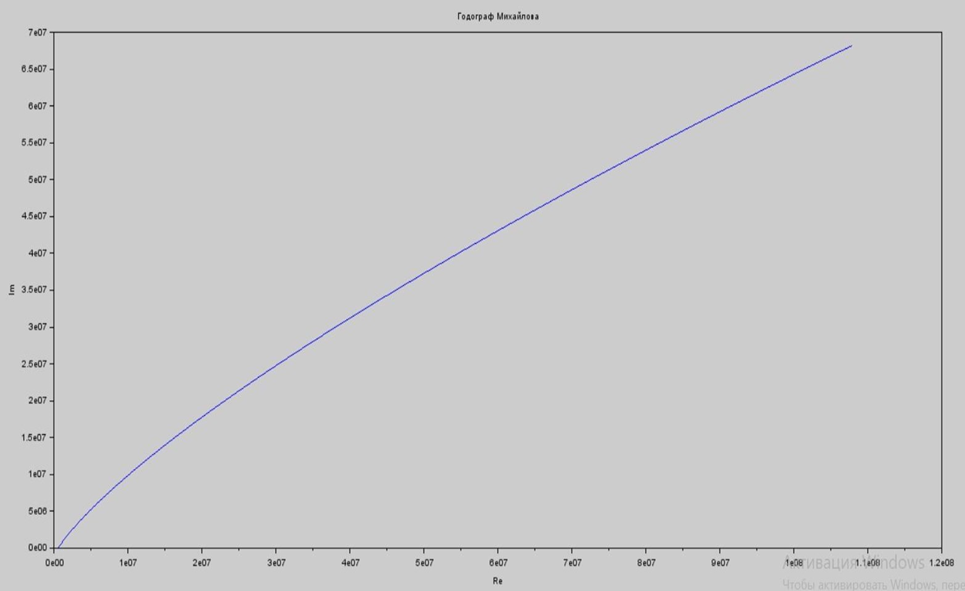 Рисунок 6.6 – Годограф Михайлова Условие устойчивости не выполняется, следовательно, система неустойчива.  Рисунок 6.7 – Программный код для построения годографа Михайлова 6.3 Критерий Гурвица Для того чтобы система была устойчива, необходимо и достаточно, чтобы определители Гурвица, составленные из коэффициентов ее характеристического уравнения, при a0 > 0 были также больше нуля. Характеристическое уравнение замкнутой системы определяется как приравненный нулю знаменатель передаточной функции замкнутой же системы. Характеристическое уравнение:
Коэффициенты:
Первое условие выполняется, так как а0 > 0. Вычислим определители:
Т.к. не все определители положительные, то система не устойчива. На рисунке 6.8 представлен используемый для расчета программный код. 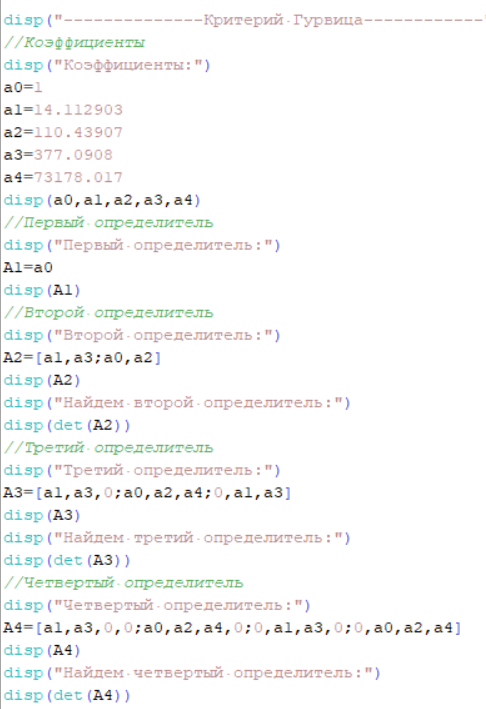 Рисунок 6.8 – Программный код для расчета определителей по критерию Гурвица 6.4 Критерий Рауса Для того чтобы система была устойчива, необходимо и достаточно чтобы все коэффициенты передаточной функции замкнутой системы, находящиеся в первом столбце таблицы Рауса были положительны. Характеристическое уравнение для замкнутой системы:
В таблице 6.1 представлены коэффициенты характеристического уравнения для замкнутой системы. Таблица 6.1 – Таблица Рауса
Рассчитаем коэффициенты из таблицы 6.1. Полученные результаты представлены в таблице 6.2. Таблица 6.2 – Результаты вычислений таблицы Рауса
Среди коэффициентов первого столбца есть те, которые меньше нуля. Условие не выполняется, следовательно, система не устойчива. 7 Коррекция устойчивости системы Построим ЛАЧХ исходной системы. На рисунке 7.1 изображена ЛАЧХ разомкнутой системы. На рисунке 7.2 изображена ЛАЧХ замкнутой системы. На рисунке 7.3 представлен необходимый для их построения программный код. 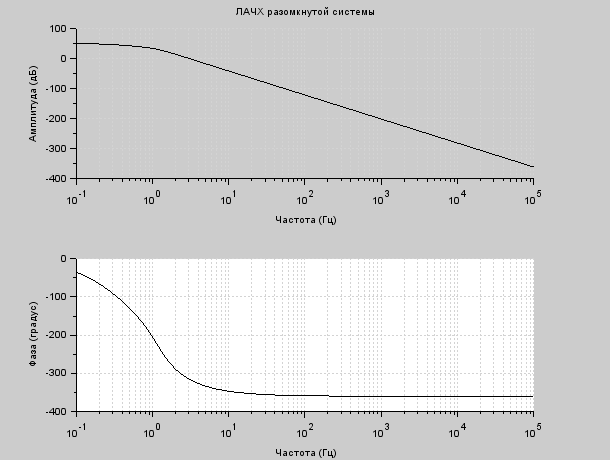 Рисунок 7.1 – ЛАЧХ разомкнутой системы 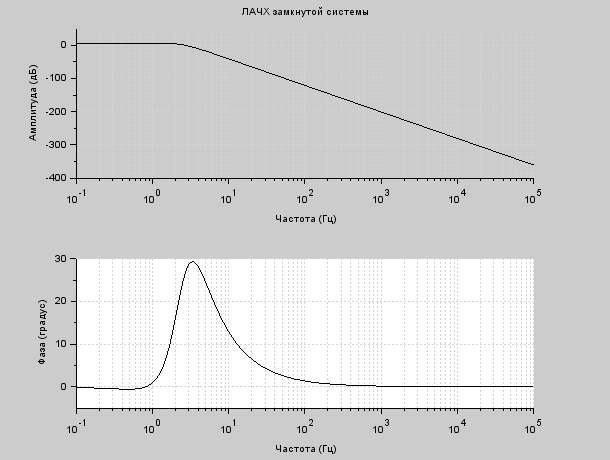 Рисунок 7.2 – ЛАЧХ замкнутой системы  Рисунок 7.3 – Программный код для построения исходной ЛАЧХ Построим желаемую ЛАЧХ. Найдем частоту среза с помощью номограмм Солодовникова, используя исходные данные tрег = 0,72 с, m = 50 %. На рисунке 7.4 представлена зависимость времени регулирования и величины перерегулирования от значения функции. На рисунке 7.5 изображена зависимость запасов устойчивости от управляющего воздействия. 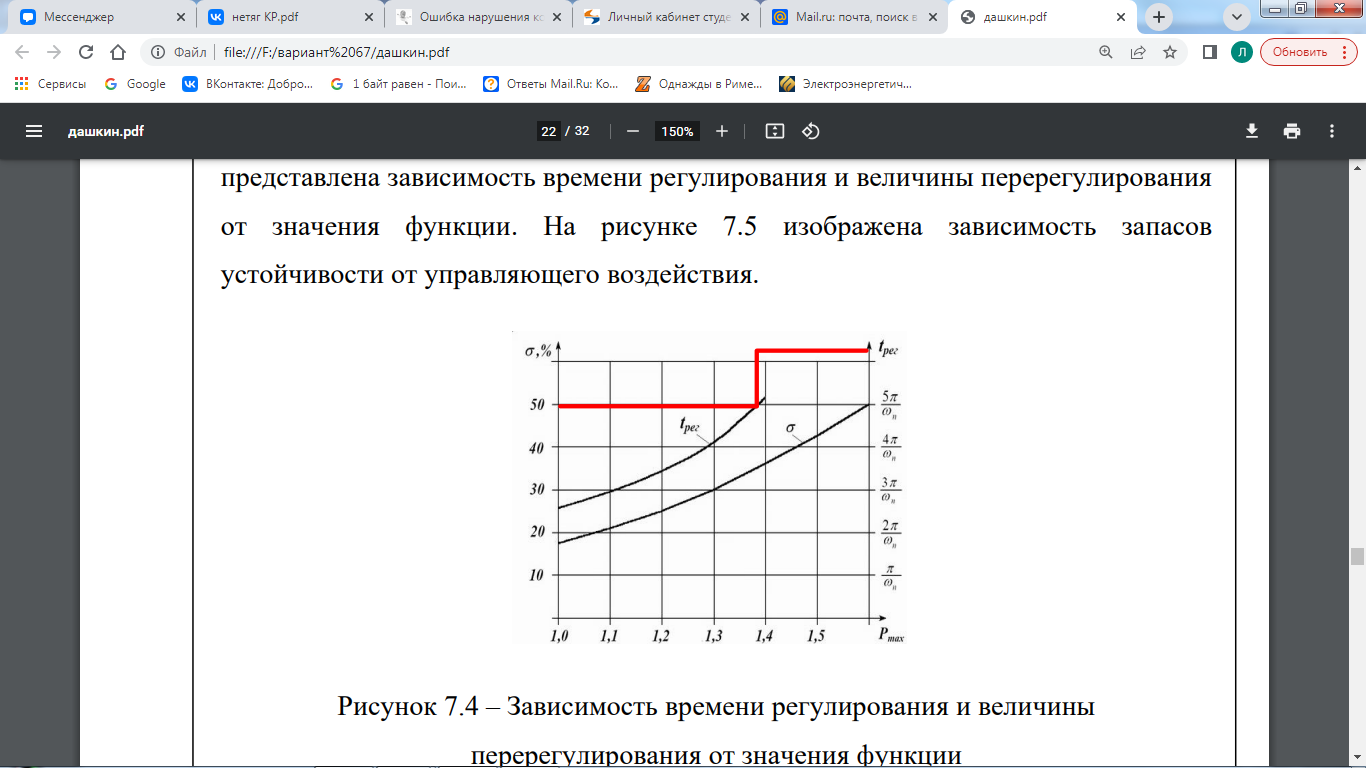 Рисунок 7.4 – Зависимость времени регулирования и величины перерегулирования от значения функции 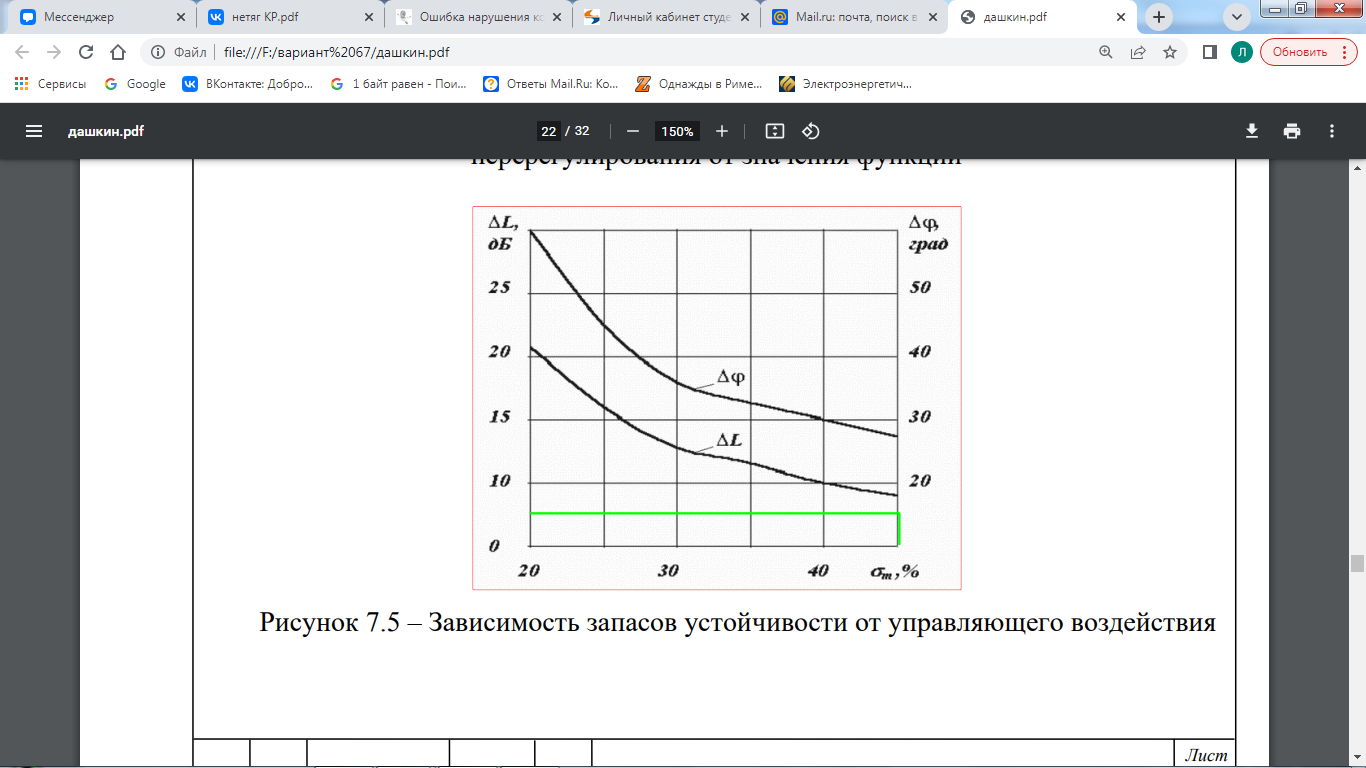 Рисунок 7.5 – Зависимость запасов устойчивости от управляющего воздействия Используя графики (рис. 7.4 и рис. 7.5) и программный код, изображенный на рис. 7.6, определим коэффициент усиления в дБ и частоту среза. Построим график желаемой ЛАЧХ (рис. 7.8). Для этого необходимо при помощи номограмм Солодовникова построить низкочастотную, среднечастотную и высокочастотную части ЛАЧХ. Коэффициент усиления определяется из числителя выражения (5.1): K = 375  Рисунок 7.6 – Программный код для расчета частоты среза 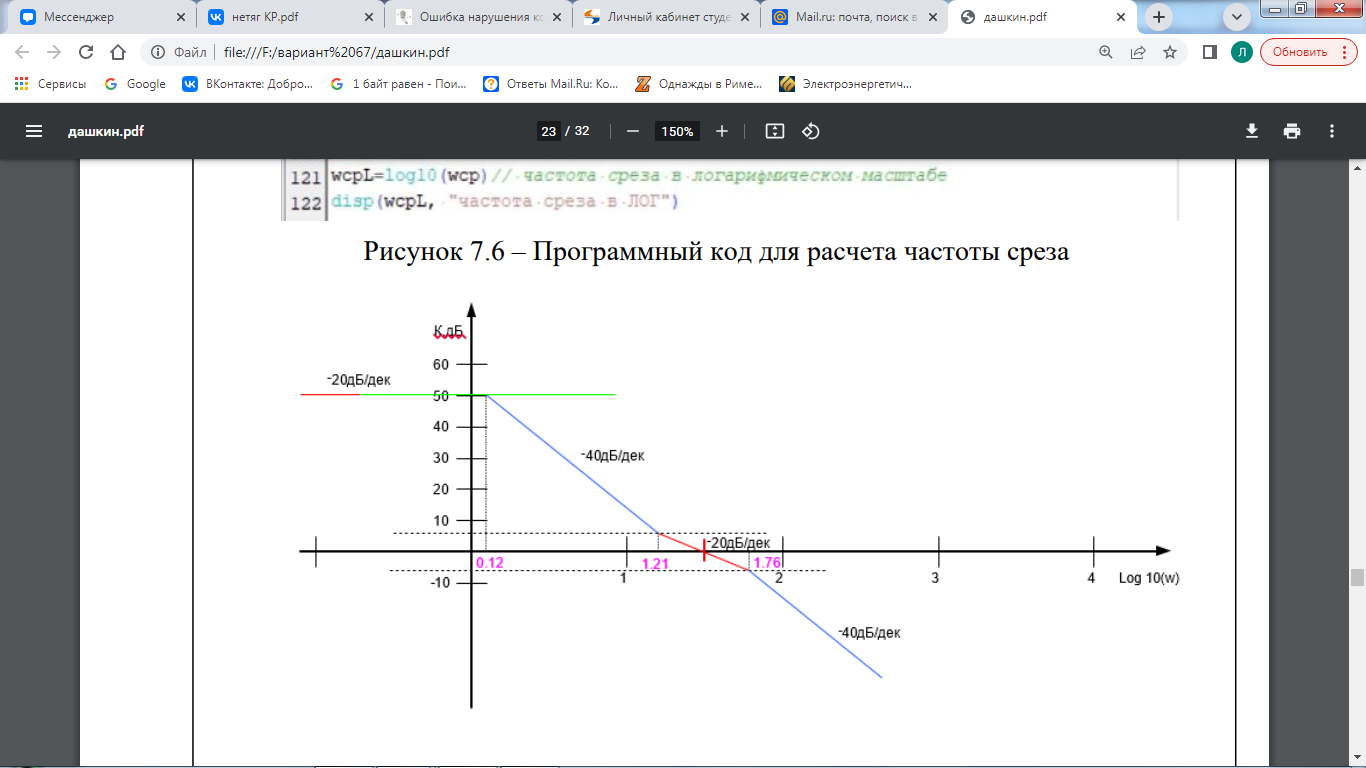 Рисунок 7.7 – Желаемая ЛАЧХ Полученная ЛАЧХ присуща астатическим САУ с астатизмом 1-го порядка. Исходя из полученных графиков определим постоянные времени системы
Т1 = 1,3182567 с; Т2 = 0,1096478 с; Т3 = 0,0380189 с. На рисунке 7.8 представлен используемый для этого расчета программный код. 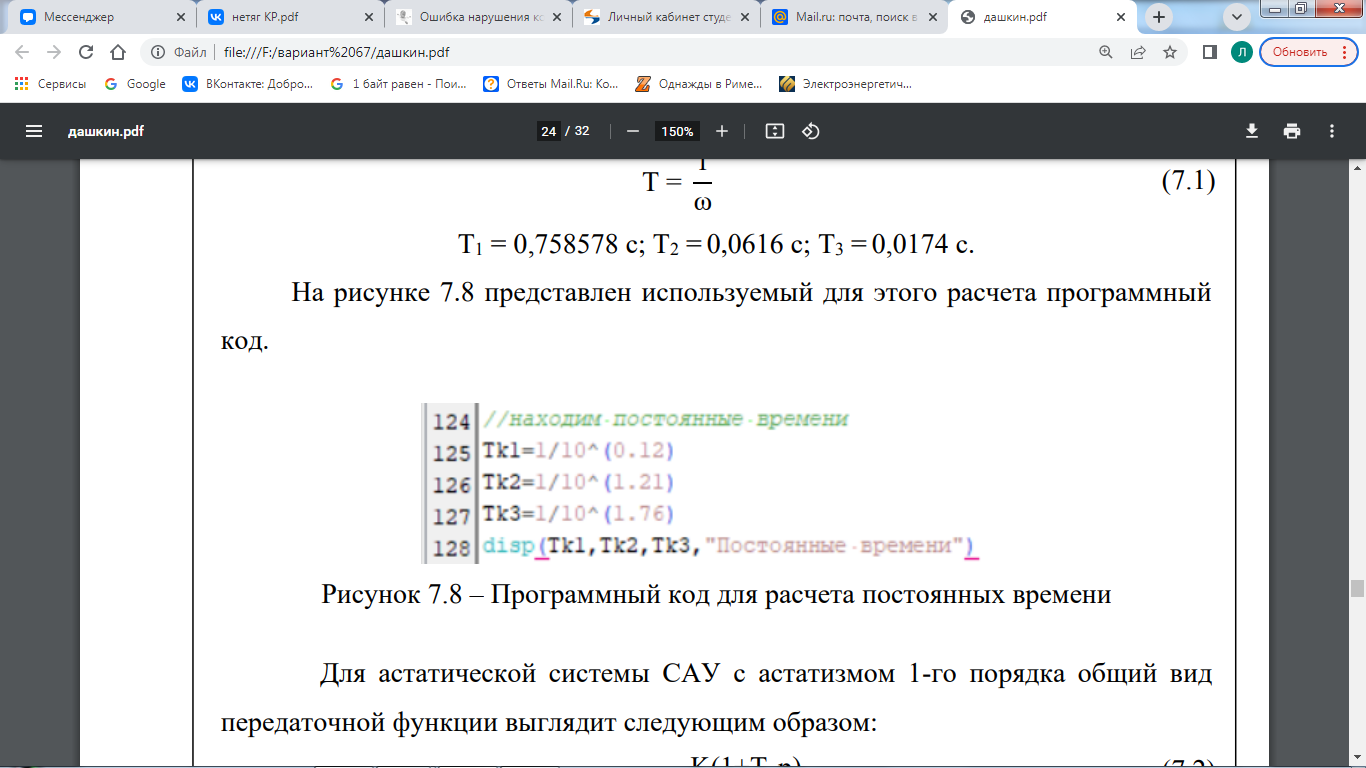 Рисунок 7.8 – Программный код для расчета постоянных времени Для астатической системы САУ с астатизмом 1-го порядка общий вид передаточной функции выглядит следующим образом:
Запишем и рассчитаем передаточные функции для звеньев откорректированной системы. Затем найдем передаточную функцию всей системы. На рисунке 7.9 представлен необходимый для этого программный код.
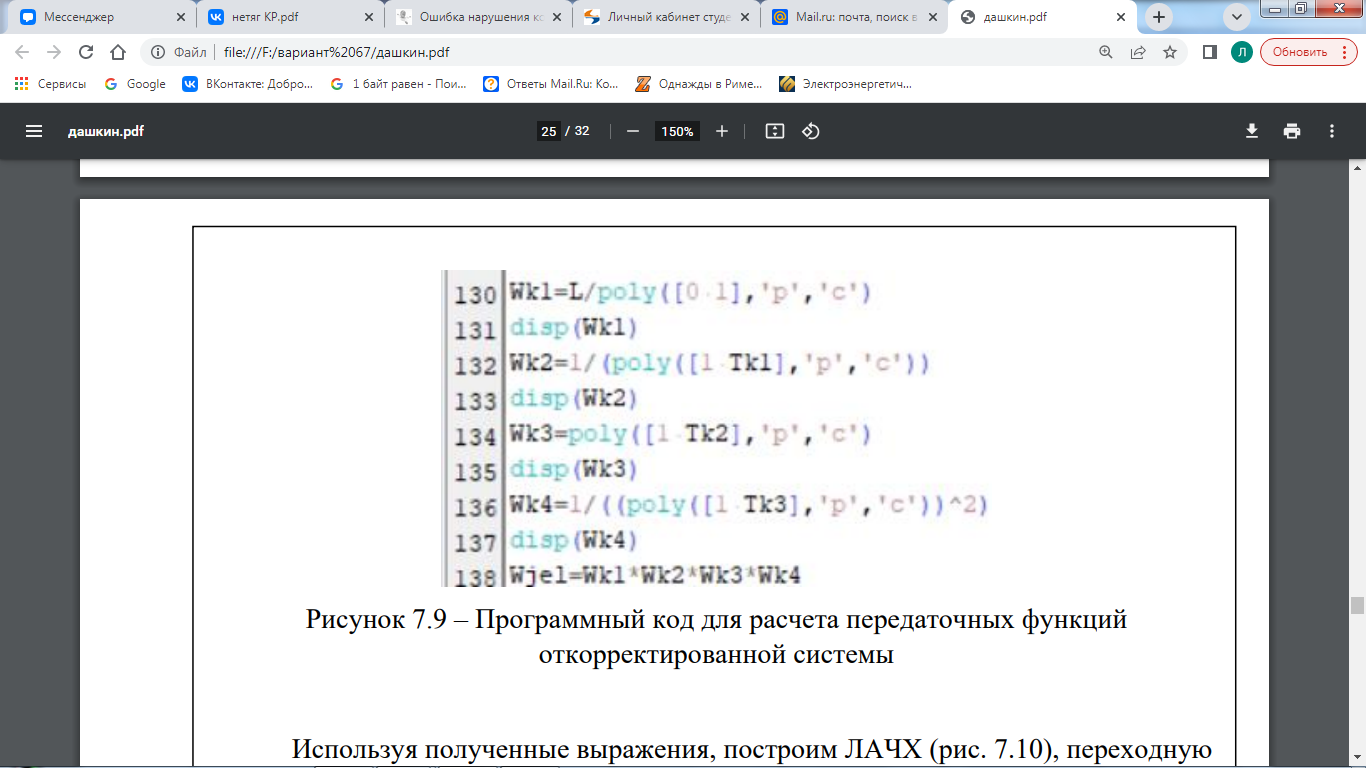 Рисунок 7.9 – Программный код для расчета передаточных функций откорректированной системы Используя полученные выражения, построим ЛАЧХ (рис. 7.10), переходную характеристику (рис. 7.11) скорректированной системы в Scilab. Необходимый для этого программный код представлен на рисунке 6.12. 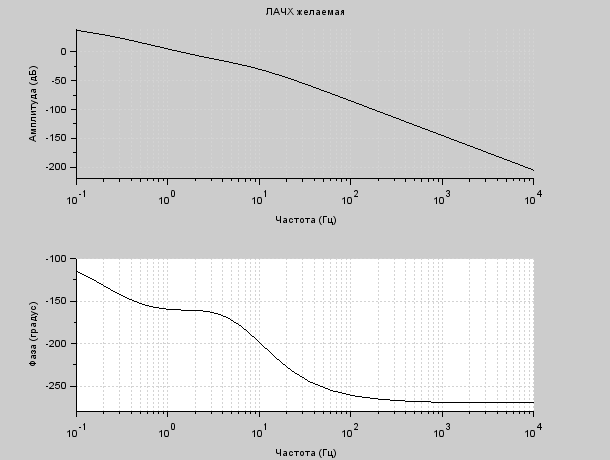 Рисунок 7.10 – ЛАЧХ скорректированной системы 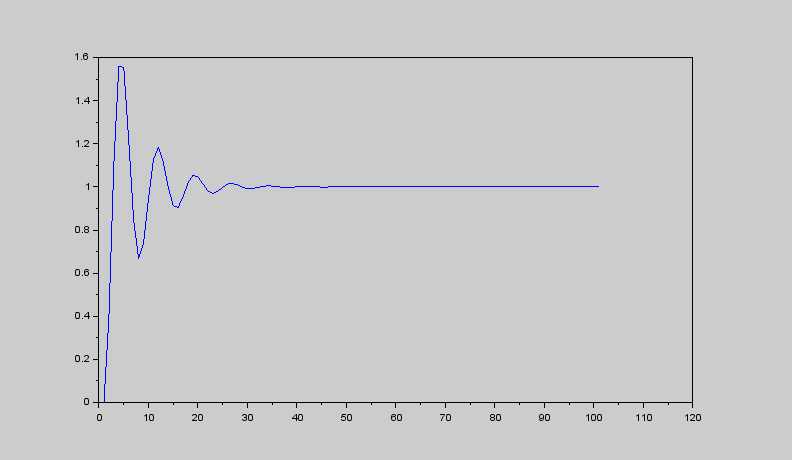 Рисунок 7.11 – Переходная характеристика скорректированной системы  Рисунок 7.12 – Программный код для построения ЛАЧХ и передаточной функции скорректированной системы Для получения желаемых характеристик систему авторегулирования необходимо скорректировать. Коррекция САР достигается посредством введения в систему дополнительных, так называемых корректирующих элементов (устройств), охватывающих один или несколько элементов исходной системы. Если направления сигналов (воздействий) в корректирующем устройстве совпадает с направлением сигналов в охватываемых им элементах, то связь называют прямой. Передаточная функция упреждающего корректирующего устройства определяется следующим образом:
АЧХ необходимого регулирующего устройства изображена на рисунке 7.13. Программный код для ее построения приведен на рисунке 7.14. 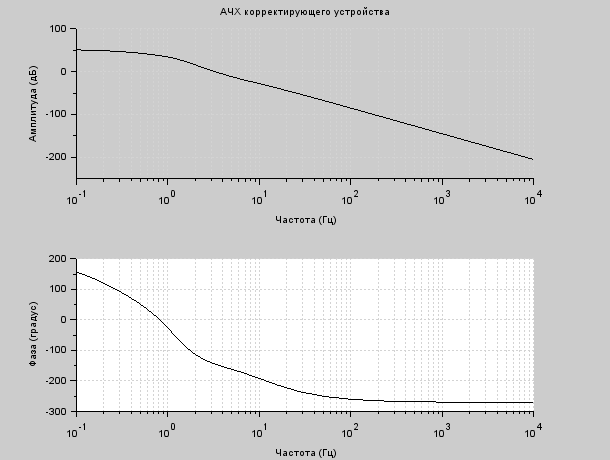 Рисунок 7.13 - АЧХ корректирующего устройства  Рисунок 7.14 – Программный код для вычисления передаточной функции корректирующего устройства и построения его АЧХ Использование корректирующего устройства с рассчитанными параметрами позволяет сделать САР устойчивой, что необходимо для нормальной и длительной работы этой системы. Передаточная функция желаемой системы определяется произведением передаточных функций разомкнутой (исходной) системы и корректирующего устройства. 8 Реализация моделирования САУ в программе SamSim Для того, чтобы наглядно убедиться, что данная система устойчива, воспользуемся программой SamSim. Программа SamSim предназначена для моделирования линейных и нелинейных цепей автоматического управления. Работает с моделями, которые можно представить в форме блок-схем. 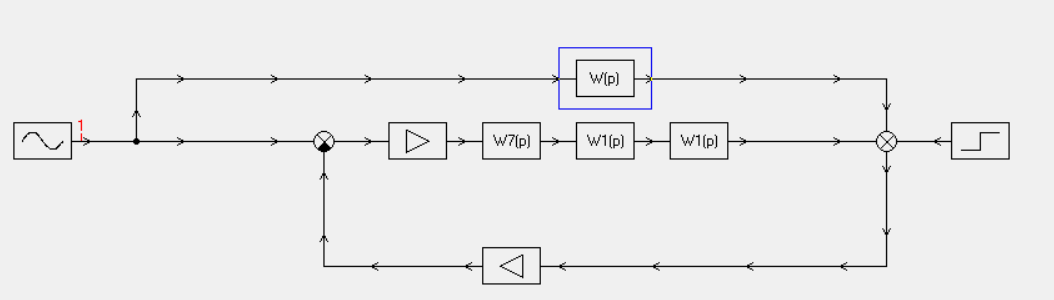 Рисунок 8.1 – Структурная схема САУ в программе SamSim 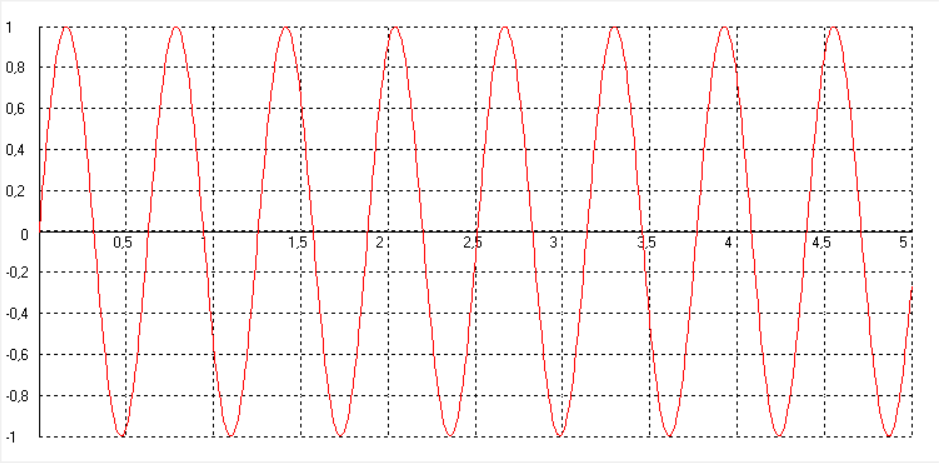 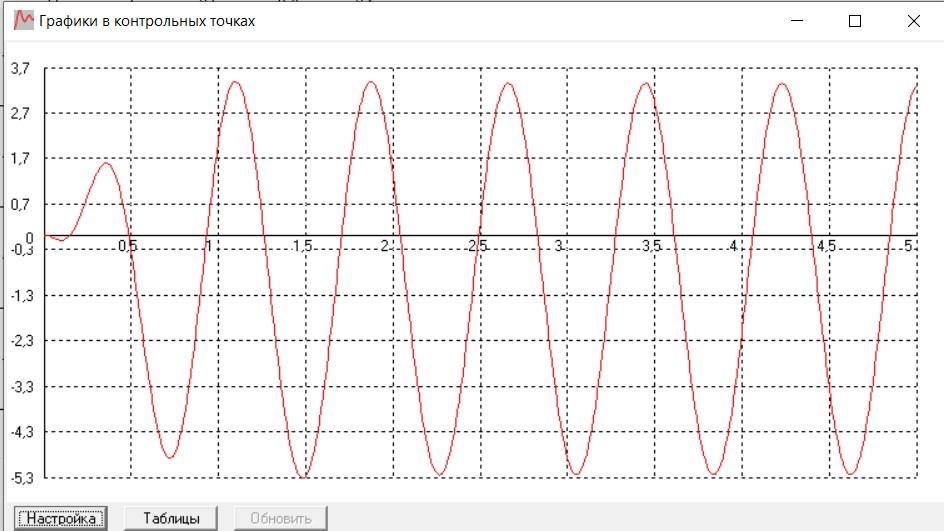     Рисунок 8.2 – График скорректированной системы Так как график САУ, реализованный в программе электронного моделирования SamSim, представляет собой ограниченную невозрастающую синусоиду, делаем вывод, что данная система устойчива. Заключение В ходе выполнения курсового проекта были выполнены все необходимые пункты, а именно: 1. Дано краткое описание работы САУ; 2. Система разбита на элементы; 3. Построена структурная схема САУ; 4. Выведены выражения для передаточных функций системы в разомкнутом и замкнутом состояниях по управляющему и возмущающему воздействиям; 5. Система проверена на устойчивость по критериям устойчивости; 6. Система откорректирована на устойчивость; 7. Реализовано моделирование САУ в SamSim. В процессе работы было проведено исследование предложенной системы автоматического регулирования с точки зрения её устойчивости и качества процесса регулирования. Согласно критериям, исходная система неустойчива. Были проведены дополнительные расчёты для подбора корректирующего элемента, рассчитаны постоянные времени, с помощью которых исходная система стала устойчивой. Так же был получен опыт разработки систем автоматического регулирования и работы c программой Scilab, а также с программой SamSim. Список использованных источников
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

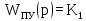
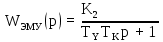
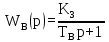
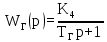
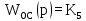
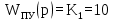
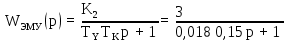
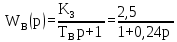
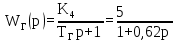
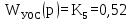
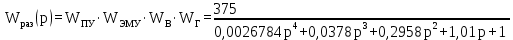
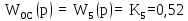
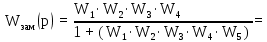
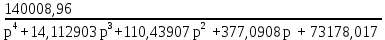
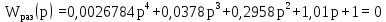
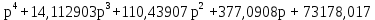 =0
=0