золотое сечение округ. Автор Выдрин Максим, учащийся 7 К класса. Научный
 Скачать 1.25 Mb. Скачать 1.25 Mb.
|
|
Государственное бюджетное общеобразовательное учреждение Средняя общеобразовательная школа № 1 С.Приволжье Приволжского района Самарской области Проект по математике Золотое сечение в природе и жизни человека Автор: Выдрин Максим, учащийся 7 «К» класса. Научный руководитель :Яшина Э.А. Учитель ФГ , С. Приволжье 2022год Оглавление 1.Введение _____________________________________с.2 2.Определение «золотого сечения»___________________с.4 3.История возникновения «золотого сечения»__________с.5 4.Золтое сечение в окружающем мире_________________с.7 5.Проявления золотого сечения______________________с.9 6.Золотое сечение в архитектуре_____________________с.12 7.Практическая значимость________________________с.14 9.Используемая литература_________________________с.15 10.Исследовательская часть_________________________с.16 Введение. Я очень люблю читать, поэтому часто посещаю библиотеки и читаю много дополнительной литературы. В одном таком источнике я прочитал такое высказывание Иоганна Кеплера: «Геометрия владеет двумя сокровищами: одно из них – это терема Пифагора, а другое – деление отрезка в крайнем и среднем отношении. … Первое можно сравнить с мерой золота, второе же больше напоминает драгоценный камень» .Что такое теорема Пифагора я уже знаю, а вот про второе сокровище мне стало очень интересно: что же такого драгоценного в делении отрезка? Мы видим окружающие нас предметы различные по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определённом отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе. Цель: Выявить правило «золотого сечения» в окружающем нас мире . Задачи: 1.Найти материал по данной теме в литературных источниках и в сети Интернет. 2. Изучить понятие « золотого сечения». 3. Составить план - конспект по данной теме. 4. Исследовать наличие «золотого сечения» в окружающем нас мире. 5. Изучить практическое применение этого правила, сделать вывод. 6 .Представить данный проект на конференции. Объект исследования: правило «золотого сечения». Предмет исследования: Окружающая среда. Актуальность: Актуальность данного материала состоит в том ,что многие окружающие нас предметы и организмы подчиняются правилу золотого сечения. С давних пор так повелось, что все самое лучшее, хорошее люди называли «золотым»: -« золотое» сердце -« золотые» руки - «золотой» характер Наши предки тоже стремились окружать себя красивыми вещами, показывали свое стремление к красоте. На отдельном этапе своего развития человек начал задаваться вопросом: почему тот или иной предмет является красивым и что является основой прекрасного? Человек различает окружающие его предметы по цвету , запаху , вкусу ,форме. Интерес к форме какого -либо предмета вызван его формой, в основе которой лежит сочетание симметрии и золотого сечения, что способствует наилучшему зрительному восприятию ощущения красоты и гармонии . В дошедшей до нас древней литературе впервые упоминание о золотом сечении встречается в трудах Евклида около 300 лет до н.э. О золотом сечении знали еще в Древнем Египте, Индии, Китае. Пропорции Пирамиды Хеопса ,храмов, предметов быта, украшений свидетельствуют о том, что Египетские мастера при построении зданий ,храмов и при изготовлении различных предметов пользовались золотым сечением. Гипотеза В основе древнерусской числовой системы заложены пропорции золотого сечения, поэтому архитектурные конструкции, создаваемые по древнерусским мерам длины, являются гармоничными и соразмерными человеческому телу. Мы предполагаем, что везде, где используется Золотое сечение получается правильное и красивое изображение, то есть красота и гармония. Мы считаем, что можно найти новый способ использования Золотого сечения в жизни человека. Определение «золотого сечения» Мне стало интересно- что же такое золотое сечение? Из Литературных источников я узнал , «золотое сечение» -это деление отрезка на две неравные части . Золотое сечение – гармоническая пропорция В математике пропорцией (лат. proportio) называют равенство двух отношений: a : b = c : d. Золотое сечение – это такое пропорциональное деление отрезка на неравные части , при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему: a : b = b : c или c : b = b : a. 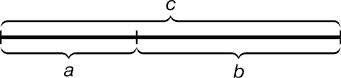 Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE = 0,618..., если AB принять за единицу, BE = 0,382... Для практических целей часто используют приближённые значения 0,62 и 0,38. Если отрезок AB принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям. История возникновения золотого сечения Принято считать, что понятие о золотом делении ввёл в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор своё знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашёл, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображённый на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления. Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.  Динамические прямоугольники Платон (427...347 гг. до н.э.) также знал о золотом делении. Его диалог «Тимей» посвящён математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления. В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления. 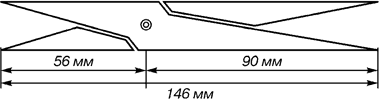 Античный циркуль золотого сечения В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» даётся геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвящённым. В эпоху Возрождения усиливается интерес к золотому делению среди учёных и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи, художник и учёный, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное. Великий астроном XVI в. Иоганн Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение). Кеплер называл золотую пропорцию продолжающей саму себя «Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причём та же пропорция сохраняется до бесконечности». Золотое сечение в окружающем мире Золотые пропорции в частях тела человека 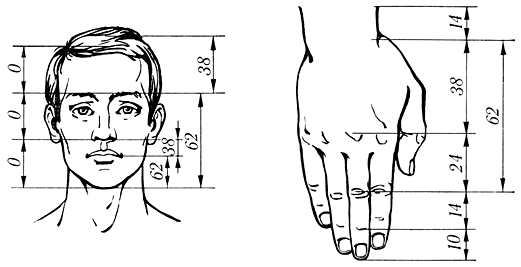  Золотые пропорции в фигуре человека Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришёл к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорождённого пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д. Справедливость своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона Бельведерского. Подверглись исследованию греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные инструменты. В конце XIX - начале XX вв. появилось немало формалистических теорий о применении золотого сечения в произведениях искусства и архитектуры. С развитием дизайна и технической эстетики действие закона золотого сечения распространилось на конструирование машин, мебели и т.д. Проявления золотого сечения.Ряд Фибоначчи С историей золотого сечения косвенным образом связано имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи (сын Боначчи). Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами. В 1202 г. вышел в свет его математический труд «Книга об абаке» (счётной доске), в котором были собраны все известные на то время задачи. Одна из задач гласила «Сколько пар кроликов в один год от одной пары родится». Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр: Месяцы 0 1 2 3 4 5 6 7 8 9 10 11 12 и т.д. Пары кроликов 0 1 1 2 3 5 8 13 21 34 55 89 144 и т.д. Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый её член, начиная с третьего, равен сумме двух предыдущих: 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34 : 55 = 0,618. Это отношение обозначается символом Ф. Только это отношение – 0,618 : 0,382 – даёт непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему Золотое сечение признано универсальным законом живых организмов. Можно отметить 2 вида проявления золотого сечения: - отношения частей целого как 62 к 38 - по числам Фибоначчи Этот ряд вывел итальянский математик Фибоначчи: 0 1 1 2 3 5 8 13 21 34 55…… Этот ряд чисел обозначает, что сумма двух предыдущих чисел дает последующее. Это спиралевидная форма проявления золотого сечения. Классическим примером золотого сечения по числам Фибоначчи является раковина моллюска Наутилус, можно увидеть его в спиралях ,по которым закручены галактики Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления. Всё, что приобретало какую-то форму, образовывалось, росло, стремилось занять место в пространстве и сохранить себя. Это стремление находит осуществление в основном в двух вариантах – рост вверх или расстилание по поверхности земли и закручивание по спирали. Раковина закручена по спирали. Если её развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см. Спирали очень распространены в природе.  Спираль Архимеда Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал её и вывел уравнение спирали. Спираль, вычерченная по этому уравнению, называется его именем. Увеличение её шага всегда равномерно. В настоящее время спираль Архимеда широко применяется в технике. Ещё Гёте подчёркивал тенденцию природы к спиральности. Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Совместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке (филлотаксис), семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения. Паук плетёт паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНК закручена двойной спиралью. Гёте называл спираль «кривой жизни». У человека на макушке головы рост волос имеет форму спирали. У каждого из нас на пальцах есть своеобразные узоры ,которые тоже имеют форму спирали. Форма уха имеет типичную форму спирали, с внешней стороны локтя мы так же можем наблюдать линии, закручены в форме спирали. Среди придорожных трав растёт ничем не примечательное растение – цикорий. Приглядимся к нему внимательно. От основного стебля образовался отросток. Тут же расположился первый листок. Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок ещё меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвёртый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определённые пропорции. 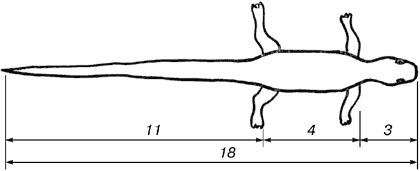 Ящерица живородящая В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции – длина её хвоста так относится к длине остального тела, как 62 к 38. И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы – симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста. Расположение листьев на стебле растений например, золотой ус , традесканция, алоэ – соответствует принципу золотого сечения. Расстояние между почками имеет соотношение как: 62 к 38. Кроме этого мы наблюдаем винтообразное расположение листьев. При таком расположении листьев достигается максимальное восприятие ими солнечных лучей , Природа осуществила деление на симметричные части и золотые пропорции. В частях проявляется повторение строения целого. Не случайно установлено, что форма яиц попадает под правило золотого сечения, что говорит о высокой прочности яичной скорлупы. 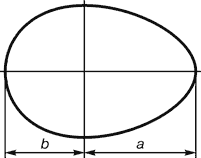 Яйцо птицы Совершенна форма стрекозы, которая тоже создана по законам золотой пропорции. Узоры на крыльях у бабочки тоже подчинены закону золотого сечения . Пьер Кюри в начале нашего столетия сформулировал ряд глубоких идей симметрии. Он утверждал, что нельзя рассматривать симметрию какого-либо тела, не учитывая симметрию окружающей среды. Золотое сечение нельзя рассматривать само по себе, отдельно, без связи с симметрией. Великий русский кристаллограф Г.В. Вульф (1863...1925) считал золотое сечение одним из проявлений симметрии. Золотое сечение в архитектуре  Архитектура Парфенона – классический пример золотого сечения. Храм Василия Блаженного на Красной площади отличается разнообразием форм и деталей, красочных покрытий. Исследуя архитектуру, пришли к выводу о преобладании в нем ряда пропорций золотого сечения, которая объединяет все 8 куполов в единую композицию.  Здание вокзала в городе Сасово не впечатляет так, как предыдущие примеры архитектуры. Но и при его строительстве была использована золотая пропорция.  Также как и в архитектуре краеведческого музея города Сасово.   Практическая значимостьПрактическая значимость моей работы заключается в том, что изученное мной золотое сечение имеет широкое применение в окружающем нас мире. Зная это правило, человек может применить его при строительстве зданий, различных сооружений, изготовлении украшений. Когда мы видим красоту различных растений или животных, их замысловатые формы, красивые и интересные постройки, то мне уже понятно, что их форма создана по правилу золотого сечения. Используя соответствующую литературу и ресурсы интернета, я очень много интересного узнал по данной теме. Меня заинтересовала тема применения золотого сечения в архитектуре. И я хотел бы найти конкретные примеры применения золотого сечения в архитектуре своего родного села и доказать это применение. И это будет тема моей следующей исследовательской работы. Вывод: Золотое сечение- естественное явление в природе и признано универсальным законом живых организмов. Используемая литературыКовалёв Ф.В. Золотое сечение в живописи. – К.: Высшая школа, 1989. Кеплер И. О шестиугольных снежинках / Пер. с латинского Ю.А. Данилова. – М.: Наука, 1982. Дюрер А. Дневники, письма, трактаты. – М.: Искусство, 1957. Стахов А.П. Коды золотой пропорции. – М.: Радио и связь, 1984. Ресурсы Интернета Ознакомившись с данным материалом в литературных источниках и в сети интернет я решил провести своё собственное исследование и выявить, где ещё в теле человека можно видеть применение золотого сечения и выяснить, где в обычной жизни людей находит применение этого правила в двух её проявлениях: 1. Деление отрезка на две неравные части как 62:38. 2. По ряду чисел Фибоначчи т.е. «Золотая спираль Архимеда» Вначале я решил выявить, где ещё в теле человека имеется применение золотого сечения и золотой спирали. Я исследовал подушечки пальцев, рисунок наружного локтевого сгиба, рост волосяных луковиц на макушке головы и исследовал форму ушей людей. Данные исследования я проводил в своей школе и взял образцы одного класса – 3 «К» в котором 20 учеников Вместе с нашей школьной мед. сестрой Ольгой Викторовной мы исследовали 20 учеников и я составил таблицу куда занёс измерительные данные. Исследование №1 «Исследование формы рисунка на подушечках пальцев» Цель: Выявить проявления золотого сечения в форме узора на подушечках пальцев. Образец рисунка брал у каждого ученика с одного пальца – указательного. Для этого я приготовил штемпельную подушку и пронумерованные листочки 5х5 см. Каждый ученик вначале делал отплиск на штемпельной подушке, а затем ставил отпечаток на листке. Рассмотрев и изучив все данные этого исследования я сделал соответствующий вывод: -Из двадцати исследованных образцов у двадцати учащихся имеются узоры на подушечках пальцев в виде завитков, образующих спираль. Увеличив образцы и сравнив их с эталоном Золотой спирали Архимеда, я сделал вывод , что они почти идентично, а значит узор на наших пальцах подчиняется правилу золотого сечения. Исследование №2 |
| Дом 62:38 | Школа 62:38 |
| Телевизор | 1. Школьное здание |
| Телефон | 2. Школьная доска |
| Форма двери | 3. Принтер |
| Шкаф | 4. Парта |
| Картина Стол | 5. Дневник 6. Ноутбук |
| Банковские карточки | 7. Учебник |
| Форма дома | 8. Блокнот |
Вывод:
Формы исследуемых мной предметов в той или иной мере созданы человеком применяя правило золотого сечения – деления отрезка на 2 неравные части соотношение сторон 62:38 и теперь я знаю, почему банкиры называют свои карточки золотыми.
Заключение
Сравнив размеры предметов с соотношениям их длин, по золотому правилу я увидел ,что люди применили правило золотого сечения.
Закономерность явлений и объектов живой природы можно объяснить с математической точки зрения. А именно существование закономерности деления отрезка и закономерности расположения в виде спирали в окружающем нас мире - мною доказаны.
Формы и размеры живых организмов созданных природой, люди используют эти знания для создания новых предметов быта ,в строительстве.


