Автореферат дисертації на здобуття наукового ступеня кандидата технічних наук Харків 2012 Дисертацією є рукопис
 Скачать 1.02 Mb.
|
|
У третьому розділі викладено результати досліджень, спрямованих на розробку нового методу хамелеон-гешування, який ґрунтується на криптографічних перетвореннях у групі точок ЕК. Визначено, що під методом хамелеон-гешування розуміється спосіб формування та перевіряння геш-значення, який використовує функцію гешування, що є колізійно-стійкою без знання особистого ключа одержувача (геш-хамелеон), володіє властивостями "непередаваність геш-значення" та "прихованість повідомлення", і може бути поданий у вигляді сукупності кроків та операцій, згрупованих у такі етапи: обчислення загальних параметрів геш-хамелеону; обчислення особистого та відкритого ключів геш-хамелеону; обчислення значення геш-хамелеону; обчислення колізії одержувачем (необов’язковий); спростування колізії підписувачем (необов’язковий). Обґрунтовані вимоги, що висуваються до методів хамелеон-гешування та критерії їх порівняння, зокрема, такі як: неінтерактивність, неможливість завчасної підробки, неспростовність, реверсивність, сумісність із алгоритмами ЕЦП, стійкість до колізій, семантична захищеність, відсутність витоку особистого ключа геш-хамелеону, використовувана математика криптографічних перетворень, сумісність із вимогами нормативних документів, можливість відмови підписувача від підробки з боку одержувача тощо. Проведено порівняльний аналіз відомих методів хамелеон-гешування, обґрунтовано необхідність створення методу хамелеон-гешування в групі точок ЕК. Доведено, що, незважаючи на те, що проблема прийняття рішення Діффі-Гелмана не розв’язувана у групі точок ЕК, яка не є суперсингулярною, як еквівалентну задачу можна застосовувати підхід, що базується на доведенні перевіряючій стороні рівності двох дискретних алгоритмів у групі точок ЕК. Доведено, що на відміну від існуючих методів хамелеон-гешування, які забезпечують субекспоненційну стійкість, запропонований метод забезпечує експоненційну стійкість. Визначено зміст етапів нового методу хамелеон-гешування (обов’язкові етапи наведені на рис. 2): На етапі 1: одержувач обирає групу точок еліптичної кривої виду:
де  – непарне,  ,  ,  .Загальносистемними параметрами геш-хамелеону є:
де функції гешування  та  визначені так:
На етапі 2: одержувач випадковим чином обирає особистий ключ  та обчислює відкритий ключ як  .На етапі 3: підписувач випадково обирає ціле число  , обчислює за виразом (4) параметр  , за виразом (5) параметр  , а також обчислює значення геш-хамелеону  (6).
де  – загальний ідентифікатор,  – ідентифікатор підписувача,  – ідентифікатор одержувача,  – ідентифікатор транзакції.
де  – повідомлення,  – абсциса точки  .На етапі 4: одержувач (із зловмисною метою) обчислює  , де:
На етапі 5: підписувач має змогу спростувати дії зловмисного одержувача за рахунок обчислення колізії. 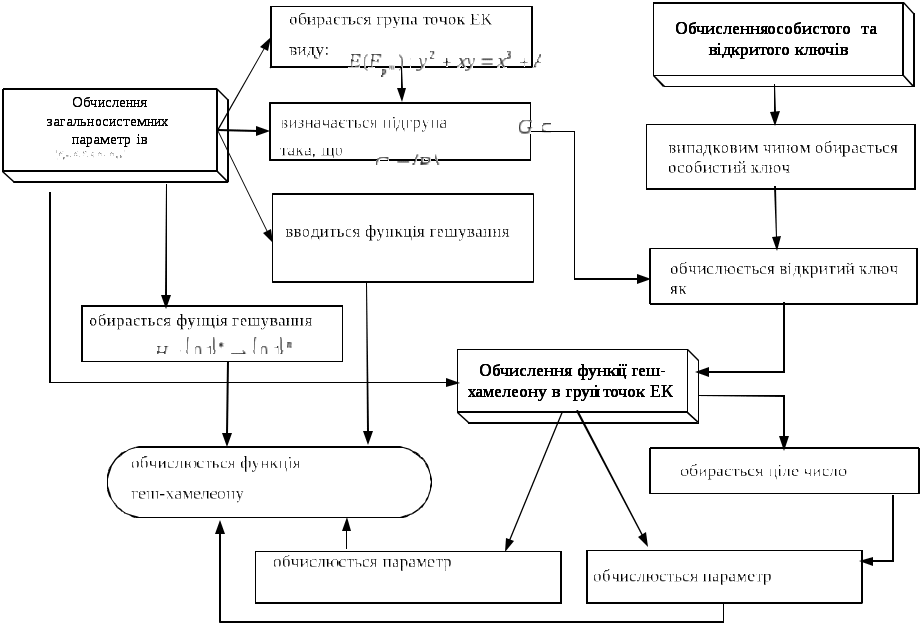 Рис. 2 – Обов’язкові етапи методу хамелеон-гешування у групі точок ЕК У четвертому розділі запропоновано вдосконалений метод ЕЦП у групі точок ЕК, що на відміну від існуючих дозволяє забезпечити криптографічну підтримку послуг приватності за рахунок використання методу хамелеон-гешування та детермінованого методу відображення бітового рядка у точку на ЕК (використовується функція Icarta). Визначено, що під вдосконаленим методом ЕЦП у групі точок ЕК розуміється спосіб формування та перевіряння ЕЦП у групі точок ЕК, що визначена над скінченним простим полем  або деяким скінченним полем  , який може бути поданий у вигляді сукупності кроків та операцій, згрупованих у такі етапи:генерація параметрів; формування ЕЦП; перевіряння ЕЦП; обчислення одержувачем колізії (необов’язковий); спростування підписувачем підробленого ЕЦП (необов’язковий). Викладаються результати досліджень, аналізуються підходи відображення бітового рядка у точку на ЕК, обґрунтовується вибір функції Icarta. Пропонується загальний вдосконалений метод ЕЦП у групі точок ЕК. Визначено, що у вдосконаленому методі ЕЦП усі параметри поділяються на загальносистемні параметри ЕЦП (згідно з стандартом ЕЦП, що обраний), параметри користувачів (підписувача та одержувача) та параметри геш-хамелеону в групі точок ЕК. Кожен користувач має свої відкриті й особисті параметри. Параметрами підписувача є: особистий ключ  та відкритий ключ  – точка на еліптичній кривій. Параметрами одержувача є: особистий ключ геш-хамелеону  та відкритий ключ геш-хамелеону  – точка на ЕК.Етап формування ЕЦП складається з таких кроків: обчислення геш-значення від повідомлення за базовим алгоритмом; обчислення функції відображення у точку на ЕК; обчислення значення геш-хамелеону обчислення на еліптичних кривих; обчислення за модулем порядку групи базової точки  .Вихідними даними процесу формування ЕЦП є пара цілих чисел  , що становлять ЕЦП, сформованих підписувачем для повідомлення  .Етап перевіряння ЕЦП складається з таких кроків: перевіряння розміру ЕЦП; обчислення геш-значення від повідомлення за базовим алгоритмом; обчислення функції відображення у точку на ЕК; обчислення значення геш-хамелеону; обчислення на еліптичних кривих; обчислення за модулем порядку групи базової точки .Якщо всі процедури проходять успішно, то ЕЦП приймається перевірником, інакше – відхиляється. Вдосконалений метод ЕЦП у групі точок ЕК включає додатковий (необов’язковий) етап "Обчислення одержувачем колізії", що виконується лише у разі виникнення протиріч. У випадку обрання базового методу ЕЦП, що використовує криптоперетворення у полі з характеристикою  рекомендовано використовувати функцію Icarta, що обчислюється за виразами (8) та (9).За умови обрання ЕК вигляду (1), функція  є бієктивним відображенням з інверсною функцією:
що дозволяє створити параметризацію підмножини ЕК  .Обчислюються координати точки на ЕК:
де  ,  ,  .Використання функції Icarta для випадку характеристики поля  дозволило вдосконалити базовий метод ЕЦП згідно з стандартом ISO/IEC 15946-2 (ECDSA) за умови використання однакових загальносистемних параметрів. У випадку обрання базового методу ЕЦП, що використовує криптоперетворення у полі з характеристикою  рекомендовано використовувати функцію Icarta, що обчислюється за виразами (10) та (11).За умови обрання ЕК вигляду:
де  ,  . Для випадку, коли – непарне, відображення є бієктивним відображенням. Обчислюються координати точки на ЕК:
де  та  . Використання функції Icarta для випадку характеристики поля 2 дозволило вдосконалити базовий метод ЕЦП згідно з стандартом ДСТУ 4145-2002 за умови використання однакових загальносистемних параметрів. У таблиці 1 наведено результати порівняльного аналізу складності базових та вдосконалених методів ЕЦП згідно з ISO/IEC 15946-2 (ECDSA) та ДСТУ 4145-2002. Таблиця 1. Результати порівняльного аналізу
У п’ятому розділі наводяться результати експериментальних досліджень (таблиця 2) швидкісних показників базового та вдосконаленого криптографічного протоколу ЕЦП за ДСТУ 4145-2002, останній з яких використовує вдосконалений метод ЕЦП. Реалізація криптографічних протоколів виконана мовою програмування Java. Тестовий стенд при цьому мав такі характеристики: операційна система Windows XP SP 3, AMD Athlon 64 X2 Dual Core Processor 3800+ 2.01Ghz, 3.00 Gb of RAM. На основі аналізу емпірично отриманих результатів визначено, що вдосконалений метод ЕЦП за ДСТУ 4145-2002, для вхідних даних невеликого обсягу удвічі повільніший від базового методу ЕЦП. Таблиця 2. Результати вимірювань швидкісних показників (мс)
У таблиці 2 під L розуміють бітову довжину порядку базової точки ЕК, під W – обсяг вхідних даних (КБ), що підписуються. Визначено, що зі збільшенням вхідного обсягу даних, від 1МБ спостерігається асимптотичне наближення швидкісних характеристик удосконаленого та базового методів ЕЦП, незалежно від бітової довжини порядку базової точки. Робляться висновки, що вирівнювання швидкісних показників зумовлене часовою складністю інкапсульованого у ДСТУ 4145-2002 методу гешування за ГОСТ 34.311-95, а також, що коректність програмної реалізації вдосконаленого методу ЕЦП за ДСТУ 4145-2002 підтверджується попарною узгодженістю функцій формування та перевіряння ЕЦП, а також функції обчислення геш-хамелеону та функції формування колізії. Формуються пропозиції щодо внесення змін до структури сертифікатів відкритого ключа, як необхідної передумови надання криптографічної підтримки послуг приватності засобами національної системи ЕЦП. Наводяться результати проектування тестового макета програмного комплексу інтернет-аукціону, що використовує вдосконалений метод ЕЦП у групі точок ЕК, у якому забезпечено властивість анонімності дій користувачів. У висновках стисло викладено основні нові наукові та практичні результати, отримані у ході дисертаційних досліджень. У додатках наведено акти впровадження отриманих результатів, запропоновані у роботі зміни до формату сертифіката відкритого ключа, проект технічного завдання на КЗЗ програмного комплексу Інтернет-аукціону. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
,
.
,
,
.
,
,
,
.
,
, 
,
,
, 
,
