Випадкові величини. Функції розподілу та їх властивості. Тема 1. Випадкові величини. Функції розподілу та їх властивості.. Тема Випадкові величини. Функції розподілу та їх властивості
 Скачать 86.06 Kb.
|
|
Тема 1. Випадкові величини. Функції розподілу та їх властивості. Оскільки результат експерименту може змінюватися від випадку до випадку, то кількісна ознака, яка в ньому розглядається, взагалі кажучи, є змінною величиною, до того ж випадковою. Отже, випадкова величина – це величина, яка в результаті експерименту з випадковим результатом набуває того чи іншого числового значення. Прикладами випадкових величин, що набувають різних числових значень під впливом багатьох випадкових факторів, можуть бути: а) кількість очок, яка випадає на верхній грані за одне кидання грального кубика; б) кількість бракованих виробів серед п навмання вибраних; в) кількість кидань монети до першої появи герба; г) кількість викликів, які надходять на телефонну станцію протягом деякого проміжку часу; д) тривалість часу обслуговування покупця; е) час виконання деякого завдання і т. д. Випадкові величини позначатимемо великими літерами X, Y, Z, …, а їхні можливі значення – малими літерами x, y, z, …, латинського алфавіту. У наведених прикладах траплялися два типи випадкових величин: дискретні величини, множини можливих значень яких скінченні або зліченні, - приклади а) – г) і неперервні величини, множини можливих значень яких суцільно заповнюють деякий інтервал, – приклади д), е) Зазначимо, що за теоретико-множинним трактуванням основних понять теорії ймовірностей випадкова величина Х є функція елементарної події: X=X(ω), де ω − елементарна подія, яка належить простору Ω(ω∈Ω). При цьому множина можливих значень випадкової величини Х складається з усіх значень, яких набуває функція X(ω). Якщо ця множина скінченна або зліченна, то випадкова величина Х називається дискретною, якщо незліченна – неперервною. Наведемо приклади дискретної і неперервної випадкових величин. Симетричну монету кидають двічі. Нехай випадкова величина Х – кількість появ герба. Простір елементарних подій складається з чотирьох елементів: Ω={ω1=(ЦЦ), ω2=(ЦГ), ω3=(ГЦ), ω4=(ГГ)}. Таблиця значень випадкової величини має такий вигляд:
2. Нехай випадкова величина Y є час очікування трамвая на зупинці. Якщо відомо, що проміжок часу між прибуттям трамваїв не перевищує Т, то значення Y належать відрізку [0,T]. Для того, щоб описати випадкову величину, необхідно вказати не тільки множину її можливих значень, а й охарактеризувати ймовірності всіх можливих подій, пов'язаних із випадковою величиною (наприклад, імовірність того, що вона набуде того чи іншого значення або потрапить у деякий інтервал). Закон розподілу ймовірностей можна подати у вигляді функції розподілу ймовірностей випадкової величини F(x), яка вже придатна як для дискретних, так і для неперервних випадкових величин Функцію аргументу x, що встановлює ймовірність випадкової події X  Її слід розуміти як функцію, яка встановлює ймовірність випадкової величини, яка може приймати значення, менші за x . Функція розподілу володіє наступними властивостями: Вона завжди додатня із значеннями в межах від нуля до одиниці  Функція є монотонно зростаючою, а саме значення функції зростають  , якщо аргументи зротають x2>x1.Із цієї властивості отримують наведені висновки: a) Імовірність набуття випадковою величиною X можливих значень з проміжку  рівна приросту її інтегральної функції F(x) на цьому проміжку: б) Імовірність, що неперервна випадкова величина X набуде конкретного можливого значення, завжди дорівнює нулю  Для неперервної випадкової величини  справджуються такі рівності: На крайніх точках неперервна випадкова величина приймає значення.   Із цих границь випливає, що для дискретної випадкової величини X з можливими значеннями з обмеженого проміжку [a;b] маємо  для   для  Наведемо розв'язки задач на відшукання функції розподілу. Приклад 1. Закон розподілу дискретної випадкової величини Х задано таблицею: 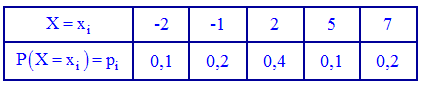 Побудувати функцію розподілу F(x) та її графік. Розв'язання. Згідно з властивостями функції F(x) отримаємо наведені дальше значення. 1)  2)  3)  4)  5)  6)  Компактно F(x) матиме запис 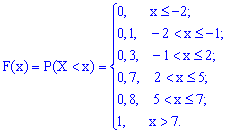 Графік функції F(x) зображено на рисунку нижче 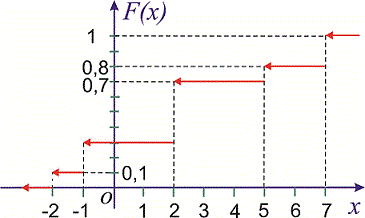 Наведений аналіз є повною відповіддю до завдання. Приклад 2. Маємо три коробки з кульками. У першому міститься 6 жовтихих і 4 сині кульки, у другому – 7 жовтиих і 3 сині, а в третьому — 2 жовті і 8 синіх. Із кожної коробки навмання беруть по одній кульці. Побудувати закон розподілу ймовірностей дискретної випадкової величини X – появи числа синіх кульок серед трьох навмання взятих; визначити закон розподілу F(x) та побудувати графік цієї функції. Розв'язання. Серед трьох навмання взятих кульок число синіх може бути 0; 1; 2; 3. У табличній формі закон розподілу дискретної випадкової величини має вигляд:  Обчислимо ймовірності p1, p2, p3, p4. Із цією метою позначимо A1 випадкову подію, що полягає відповідно в появі жовтої кульки і B1 – появі синьої з першої коробки. Подібним чином для решти коробок A2, B2, A3, B3. Імовірності цих подій такі:    Оскільки випадкові події A1, B1, A2, B2, A3, B3 є незалежними, то ймовірності знаходимо за формулами:       Обчислення достатньо прості і зроблені позначення повністю все пояснюють. Перевіримо виконання умови нормування  Завжди виконуйте перевірку даної умови: це достатньо просто зробити та дозволяє швидко перевірити правильність обчислень ймовірності. У випадках, коли умова нормування не виконується потрібно відшукати помилку та виправити її. У нас же всі обчислення правильні, тому записуємо закон розподілу ймовірностей в табличній формі:  Обчислюємо значення інтегральної функції 1)  2)  3)  4)  5)  У випадку помилок при знаходженні ймовірностей останнє співвідношення дає відмінни від одиниці результат, тому можете перевіряти і за цим значенням. Спрощено функція розподілу матиме вигляд 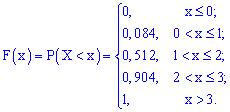 а її графік наступний 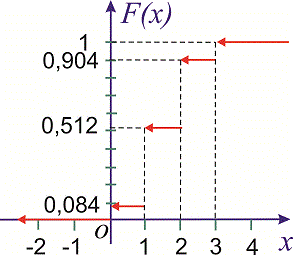 Приклад 3. Закон розподілу неперервної випадкової величини X задано функцією розподілу ймовірностей 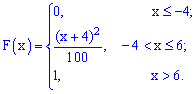 Побудувати графік функції розподілу F(X) і обчислити ймовірність, що випадкова величина належить проміжку P(1 Розв'язання. Функція розподілу матиме вигляд. 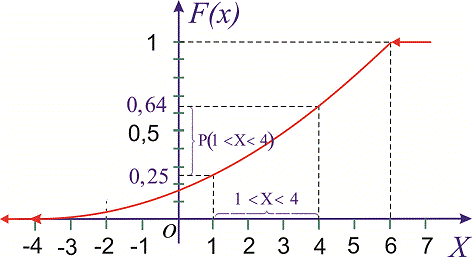 Використовуючи означення, обчислимо 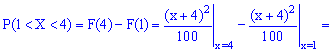  Таким чином ймовірність, що випадкова величина належить проміжку [1,4] рівна 0,36. Уважно розберіться з наведеними прикладами знаходження функції розподілу, це Вам стане в нагоді на практичних заняттях. Старайтеся перевіряти умову нормування, щоб уникнути подальших помилок і правильно визначайте ймовірності. Завдання для самостійного виконання У результаті аналізу рахунків 200 інвесторів на фондовій біржі отримали таку інформацію про кількість угод, укладених протягом місяця (див. табл. 3, у якій  – кількість укладених угод, а – кількість інвесторів).Таблиця 3
Знайти функцію розподілу кількості укладених угод та обчислити  . |