Бақберген Нұрханым 7М05308 кхд10нд. Баберген Нрханым 7М05308
 Скачать 75.91 Kb. Скачать 75.91 Kb.
|
1015 ГэВ, то можно предположить, что это вызовет распад протона, который может быть связан с супертяжелой частицей Мх = 1015 ГэВ. Поиск распада протона ведется во многих лабораториях мира. Одна из возможных мод распада р → π0 + е+. До сих пор распад протона не обнаружен. Экспериментаторы оценивают время жизни протона τр > 1033 лет.
+ А взаимодействиях.
1ф, которые позволяли сравнивать функций ф(г) для различных ядер. Рассматриваемые процессы в z представлении подтвердили энергетическую, угловую независимость и степенное поведение скейлинговой функции ф(г)
+ р и 7гБақберген Нұрханым 7М05308 КХД 18.Лагранжиан квантовой хромодинамики 22.Причина большой разницы массы адрона и суммы масс составляющих её кварков 23.Объясните значение фейнмановских диаграмм в КХД. 24.Поясните физический смысл конфайнмента и асиптотической свободы кварков. 25.Поясните, что значит бъёркеновский скейлинг партонной модели. 26.Поясните, что значит нарушения бъёркеновского скейлинга партонной модели. 27.Объясните физический смысл «бегущей константы связи» в КХД. Теория возмущений в КХД 18. Лагранжиан КХД Новая внутренняя степень свободы, цвет, означает, что кварковому полю приписывается определённый вектор состояния Поскольку группа SU(3) связна, все её элементы можно получить экспоненциированием алгебры ASU(3). Следовательно, любое вращение в C(3) можно представить в виде Далее используется стандартный принцип калибровочной инвариантности. Рассмотрим лагранжиан свободного кваркового поля Этот лагранжиан инвариантен относительно глобальных калибровочных преобразований кварковых и антикварковых полей: Если же потребовать инвариантность относительно локальных калибровочных преобразований (то есть при где Видно, что этот лагранжиан порождает наряду с вершиной взаимодействия кварк-антикварк-глюон и трёхглюонные и четырёхглюонные вершины. Иными словами, неабелевость теории привела к взаимодействию глюонов и к нелинейным уравнениям Янга-Миллса. 22. С изобретением Пузырьковой камеры и Искровой камеры в 1950-х гг., экспериментальная физика элементарных частиц обнаружила большое и постоянно растущее число частиц, названных адронами. Стало ясно, что все они не могут быть элементарными. Частицы были классифицированы по электрическому заряду и изоспину; затем (в 1953 г.) Мюрреем Гелл-Манном и Казухико Нишиджимой - по странности. Для лучшего понимания общих закономерностей адроны были объединены в группы и по другим сходным свойствам: массам, времени жизни и пр. В 1963 г. Гелл-Манн и, независимо от него, Джордж Цвейг, высказали предположение, что структура этих групп (фактически, SU(3)-мультиплепов) может быть объяснена существованием более элементарных структурных элементов внутри адронов. Эти частицы были названы кварками. Все многообразие известных на тот момент адронов могло быть построено всего из трех кварков: u d и s. Впоследствии было открыто еще три более массивных кварка. Каждый из этих кварков является носителем определенного квантого числа, названного его ароматом. Однако, в подобном описании одна частица, Δ++(1232), оказалась наделена необъяснимыми свойствами; в кварковой модели, она составлена из трех u-кварков со спинами, ориентированными в одном направлении, причем орбитальный момент их относительного движения равен нулю. Все три кварка в таком случае должны находиться в одном и том же квантовом состоянии, а так как кварк является фермионом, подобная комбинация запрещается принципом исключения Паули. В 1965 г. Моо-Юнг Хан совместно с Йохиро Намбу и Оскар В. Гринберг независимо друг от друга решили эту проблему, предположив, что кварк обладает дополнительными степенями свободы калибровочной группы SU(3), позже названными "цветовыми зарядами". Хан и Намбу отметили, что кварк взаимодействует через октет векторных калибровочных бозонов, названных глюонами (англ. "glue" - "клей"). Поскольку свободных кварков не было обнаружено, считалось, что кварки были просто удобными математическими конструкциями, а не реальными частицами. Эксперименты по глубоконеупругому рассеянию электронов на протонах и связанных нейтронах показали, что в области больших энергий рассеяние происходит на каких-то элементах внутренней структуры, имеющих значительно меньшие размеры, чем размер нуклона: Ричард Фейнман назвал эти элементы "партонами" (так как они являются частями адронов). Результаты были окончательно проверены в экспериментах в SLAC в 1969 г. Дальнейшие исследования показали, что партоны следует отождествить с кварками, а также с глюонами. 23-24. В 1968 году Ричард Фейнман показал, что его диаграммы также можно применить к сильному взаимодействию, поэтому они позволяют описывать квантовую хромодинамику, добавляя новые правила. Таким образом, фундаментальным процессом, аналогичным электрон-фотонной реакции в электродинамике, является кварк-глюонная реакция, в которой сохраняется цветовой заряд (но не аромат). У глюонов, несущих подобно кваркам цветовые заряды (в отличие от фотонов, которые являются нейтральными), есть вершины, содержащие только глюоны [33]:Вершина квантовой хромодинамики 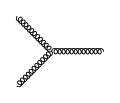   1. вершинный КХД кварк глюон 1. вершинный КХД кварк глюон2. вершинная КХД 3 глюона 3. вершинная КХД 4 глюона Изучение сильных взаимодействий с диаграммами Фейнмана возможно благодаря свойству асимптотической свободы, которое позволяет применять теорию возмущений к кваркам и глюонам: на очень коротком расстоянии это взаимодействие становится слабым. Затем определяется константа связи сильного взаимодействия для вершины, отмечено как 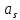 {\displaystyle \alpha _{s}} {\displaystyle \alpha _{s}}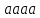 — это эквивалент постоянной тонкой структуры в квантовой электродинамике. Сложность квантовой хромодинамики связана с тем, что на кварки сильно влияют непертурбативные силы. Фиксируя на очень больших уровнях импульсов, где связь слабая, значение {\displaystyle \alpha _{s}} — это эквивалент постоянной тонкой структуры в квантовой электродинамике. Сложность квантовой хромодинамики связана с тем, что на кварки сильно влияют непертурбативные силы. Фиксируя на очень больших уровнях импульсов, где связь слабая, значение {\displaystyle \alpha _{s}}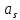 позволяет рассчитать результат процесса рассеяния при высоких энергиях. позволяет рассчитать результат процесса рассеяния при высоких энергиях.Другая сторона асимптотической свободы — конфайнмент. Так как сила взаимодействия между цветовыми зарядами не уменьшается с расстоянием, предполагается, что кварки и глюоны никогда не могут быть освобождены из адрона. Этот аспект теории подтвержден расчетами сеточной КХД, но математически не доказан. Поиск этого доказательства - одна из семи "задач тысячелетия", объявленных Математическим институтом Клэя. Другие перспективы непертурбативной КХД — исследование фаз кварковой материи, включая кварк-глюнную плазму. 25. Парто́н (от англ. part «часть») — точечноподобная составляющая адронов, проявляющаяся в экспериментах по глубоко неупругому рассеянию адронов на лептонах и других адронах. Партонная модель была предложена Ричардом Фейнманом в 1969 году[1] для анализа столкновения протонов при высоких энергиях. Партонная модель позволила объяснить результаты глубоко неупругого рассеяния электронов на протонах[2]. После экспериментального обнаружения скейлинга Бьёркена, подтверждения кварковой модели и асимптотической свободы в квантовой хромодинамике, партоны были отождествлены с кварками, антикварками и глюонами, составляющими адроны[3][4]. Партонная модель является хорошим приближением для взаимодействий адронов при высоких энергиях. Физическая интерпретация Бьеркеновского скейлинга была дана Р.Фейнманом в партои-ной модели. Открытие отклонение от партонного скейлинга, полученное в /iN рассеянии в Батавии при энергиях 56 и 150 ГэВ [66], стало указанием на существование межкварковых сил, обусловленных обменом глюо-нов, и считается одним из основных доказательством КХД. Измерение отклонения от Бьеркеновского скейлинга дает информацию о природе межкварковых сил. 26. При анализе экспериментальных данных по рождению заряженных адронов в р{р) -f р взаимодействиях, полученных коллаборациями CDF [111], UA1 [112] и ISR [ИЗ, 114], был установлен z-скейлинг [Ю]. Инклюзивное сечение рождения частиц, в рамках общей концепции г-сксйлипга, описывается в терминах безразмерной скейлинговой функции ip(z) и переменной z. Для построения if>(z) и 2 используются экспериментально измеряемые инклюзивные сечения рождения частиц (струй) и средние плотности множественности в исевдобыстротпом пространстве. Этот феноменологический подход основывается на достаточно общих физических принципах локальности, самоиодобия и фрактальности. Переменная 2 обладает свойствами фрактальной меры и описывает фрактальные свойства сталкивающихся нуклонов. Она зависит от их аномальных фрактальных размерностей Скейлинговая функция ф(г) интерпретируется как плотность вероятности образования частицы (струи) с данным значением величины г. Применение концепции .г-скейлинга для анализа экспериментальных данных по рождению прямых фотонов [14]-[16], [18J, нейтральных мезонов [2] и струй [1] в р+р и р+р взаимодействиях показало справедливость данного феноменологического подхода. Было установлено, что данные в z представлении обладают энергетической и угловой независимостью. Обнаружено существование двух областей различного поведения скей-линговой функции ф(г)\ степенное поведение функции ф(г) |
Описанные особенности z-скейлинга позволили предсказать спектры заряженных частиц, прямых фотонов, нейтральных мезонов в р + р(р), 7г
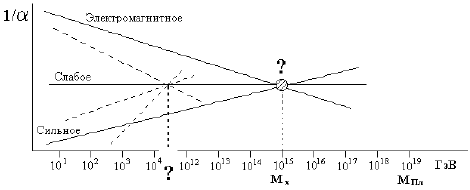 Рис. 4. Перспективы объединения взаимодействий: пунктир – возможное объединение при энергии LHC; Е – 107 ГзВ; сплошная линия – объединение при Е – 1015 ГэВ. |