Журнал Л.Р. Iкурс для студентов астрономия новое. Белгородский индустриальный колледж
 Скачать 1.26 Mb.
|
|
Министерство образования Белгородской области Областное государственное автономное профессиональное образовательное учреждение «Белгородский индустриальный колледж» Группа_____________ ЖУРНАЛ Отчётов по практическим работам по дисциплине “Астрономия ” ________________ТОЛР Студент_____________________________/______________/ Принял_____________________________/______________/ 2022 Практическая работа № 1 ОСНОВНЫЕ ЭЛЕМЕНТЫ НЕБЕСНОЙ СФЕРЫ. УСЛОВИЯ ВИДИМОСТИ СВЕТИЛ НА РАЗЛИЧНЫХ ШИРОТАХ Цель работы: изучение основных элементов и суточного вращения небесной сферы на ее модели. Знакомство с системами небесных координат. Изучение условий видимости светил на различных широтах. Оборудование: модель небесной сферы, черный глобус. Вопросы к допуску: 1. Небесная сфера, ее основные линии и плоскости. 2. Системы небесных координат. 3. Условия видимости светил на разных широтах. 4. Тест по теме: «Небесная сфера» Основные теоретические сведения Небесная сфера и ее основные элементы. Для определения видимого положения небесных тел и изучения их движения в астрономии вводится понятие небесной сферы. Сфера произвольного радиуса с центром, помещенным в произвольной точке пространства, называется небесной сферой. Вращение небесной сферы повторя- ет вращение небесного свода. Прямая ZOZ (рис. 1.), проходящая через центр О небесной сферы и совпа- дающая с направлением нити отвеса в Z  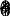 P M QE месте наблюдения, называется вертикаль- O m ной линией. N S Вертикальная линия пересекает не- бесную сферу в точках Зенита Z и Надира W Z. Q' Большой круг небесной сферы SWNE, плоскость которого перпендикулярна к вертикальной линии, называется математическим или истинным горизон- P' Z' Рис.1 Основные элементы небесной сферы том. Математический горизонт делит небесную сферу на две половины: види- мую и не видимую для наблюдателя. Диаметр РР, вокруг которого происходит вращение небесной сферы, на- зывается осью мира. Ось мира пересекается с небесной сферой в северном Pи южном P полюсах мира. Большой круг небесной сферы QWQE, плоскость ко- торого перпендикулярна к оси мира, называется небесным экватором. Небес- ный экватор делит поверхность небесной сферы на два полушария — северное и южное. Небесный экватор пересекается с математическим горизонтом в двух точках — точке востока Е и точке запада W. Большой круг небесной сферы PZQSPZQN, плоскость которого прохо- дит через отвесную линию и ось мира, называется небесным меридианом. Не- бесный меридиан делит поверхность небесной сферы на восточное и западное полушария. Плоскость небесного меридиана и плоскость математического горизонта пересекаются по прямой линии NOS, которая называется полуденной линией. Небесный меридиан пересекается с математическим горизонтом в двух точках — точке севера Nи точке юга S. Явление пересечения светилом небесного меридиана называется кульми- нацией светила. Если светило пересекает верхнюю часть меридиана наступает верхняя кульминация, если нижнюю нижняя кульминация. Дуга большого круга небесной сферы ZМZ (рис.2), проходящая через зе- нит, светило М и надир, называется кругом высот или вертикалом светила M. Круги высот, проходящие через точки востока и запада, называются пер- выми вертикалами — восточным и западным. Малый круг небесной сферы (bМb) (рис.3), плоскость которого парал- лельна плоскости небесного экватора, называется небесной или суточной па- раллелью светила. Видимые суточные движения светил совершаются по суточ- ным параллелям. Дуга большого круга небесной сферы РМР, проходящая через полюсы мира и светило М, называется часовым кругом или кругом склонения светила. Системы небесных координат. По- ложение светила на небе однозначно опре- деляется по отношению к основным плос- костям и связанным с ними линиям и точ- кам небесной сферы и выражается количе- ственно двумя величинами (центральными углами или дугами больших кругов), кото- рые называются небесными координатами. Горизонтальная система. Основ- ной плоскостью является плоскость мате- матического горизонта NWSE, а отсчет ве- Z  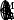 N SZ' Рис.2 Горизонтальная система координат дется от зенита и от одной из точек математического горизонта. Одной коор- динатой является зенитное расстояние z, или высота светила над горизонтом h(рис.2). Высотой hсветила М называется дуга круга высот mM от математиче- ского горизонта до светила, или центральный угол mОM между плоскостью математического горизонта и направлением на светило М. Высоты отсчитыва- ются в пределах от 0 до 90 к зениту и от 0 до -90 к надиру. Зенитным расстоянием светила называется дуга вертикального круга ZM от зенита до светила. z + h = 90 Положение самого вертикального круга определяется другой координа- той — азимутом А. Азимутом А светила называется дуга математического го- ризонта Sm от точки юга S до вертикального круга, проходящего через светило. Азимуты отсчитываются в сторону суточного вращения небесной сферы, т.е. к западу от точки юга, в пределах от 0 до 360 . Эта система координат используется для непосредственных определений види- мых положений светил с помощью угломерных инструментов. Первая экваториальная система координат. Основной плоскостью в этой системе является плоскость небесного экватора. Начало отсчета — верх- няя точка небесного экватора Q. Одной координатой является склонение.Скло- нением называется дуга mM часового круга PMmP от небесного экватора до светила. Отсчитываются склонения от 0 до +90° к северному полюсу и от 0 до - 90° к южному. Кроме склонения можно использовать полярное расстояние p — дугу от северного полюса мира до светила. р + = 90°.  Положение часового круга определя- ется часовым углом t.Часовым углом светила М называется дуга небесного экватора Qm от верхней точки Q небесного экватора до часового N круга PMmP, проходящего через светило. Часовые углы отсчитываются в сторону су- точного обращения небесной сферы, к за- Q' паду от Q, в пределах от 0 до 360° или от 0 до 24 часов. Эта система координат используется в практической астрономии для определе- ния точного времени. Z P M QE t O m S W P' Z' Рис.3 Первая экваториальная система координат Вторая экваториальная система координат. Основной плоскостью этой системы координат является плоскость небесного экватора. Одной координатой является склонение , другой прямое восхождение .  Прямым восхождением светила М называется дуга небесного экватора †m от точки весеннего равноденствия † до ча- сового круга, проходящего через светило.Отсчитываются в сторону противопо- ложную суточному вращению небесной сферы, в пределах от 0 до 360° или от 0 до N 24 часов. Эта система используется для опре- Q' деления неизменных при суточном враще- нии небесной сферы координат и составле- ния каталогов небесных объектов. Высота полюса мира над горизон- том, высота светила в меридиане. Высо- та полюса мира над горизонтом всегда рав- на географической широте места наблюдения. Z P M QE O m S W † P' Z' Рис.4 Вторая экваториальная система координат Если склонение светила меньше географической широты, то оно кульми- нирует к югу от зенита на зенитном расстоянии z = , или на высоте h = 90° - . Если склонение светила равно географической широте, то оно кульмини- рует в зените и z = 0, а h = + 90°. Если склонение светила больше географической широты, то оно кульми- нирует к северу от зенита на z = или на высоте: h = 90° + . Условия для восхода и заката светил. Если мы внимательно понаблюдаем за суточным движением светил, то заметим, что некоторые из них восходят, проходят через небесный меридиан (кульминируют) и заходят. Другие же за горизонт не опускаются, например, созвездие Большой Медведицы на средних широтах северного полушария Земли. Древние греки даже отразили это в легенде, посвященной созвездию. Богиня Гера сделала так, что Медведица никогда не может окунуться в океан и освежиться. В то же время часть звезд юж- ной полусферы небосвода вообще никогда не восходят в северном полушарии. Можно определить точные условия восхода небесных объектов по приведен- ным ниже формулам. Светило восходит и заходит на данной широте, если < (90° - ). Светило будет незаходящим или невосходящим, если > (90° - ). Для наблюдателя на земном экваторе все светила восходящие и заходящие. На полюсах наблюдатели могут созерцать только полусферы, соответствующие данному полюсу. Для получения зачета необходимо: Свободно владеть моделью небесной сферы с целью определения на ней видимых положений светил. Уметь изобразить на чертеже небесной сферы точку с известными горизонтальными и экваториальными координатами. Знать условия видимости светил на различных географических широтах. Задания 1. Укажите названия точек и линий небесной сферы, обозначенных цифрами 1—14 на рисунке 2.1 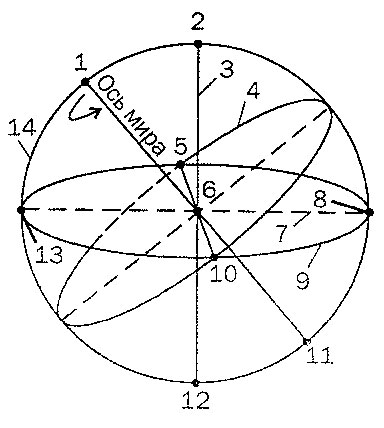 2. Используя карту звездного неба, найдите звезды по их координатам
3. Используя карту звездного неба, внесите в соответствующие графы таблицы схемы созвездий с яркими звездами. В каждом созвездии выделите наиболее яркую звезду и укажите ее название
Для получения зачета необходимо: 1. Свободно владеть моделью небесной сферы с целью определения на ней видимых положений светил. 2. Уметь изобразить на чертеже небесной сферы точку с известными горизонтальными и экваториальными координатами. 3. Знать условия видимости светил на различных географических широтах Контрольные вопросы: 1. Что является центром небесной сферы? 2. Каков радиус небесной сферы? 3. Чем отличаются небесные сферы двух соседей по парте. Выполнил: студент группы ______ ________________________________________ (ФИО) Принял: преподаватель ______________________________________________________ Дата выполнения:_____________________________________________________________ Оценка по защите : ___________________________________________________________ Практическая работа № 2 ЗАКОНЫ КЕПЛЕРА И КОНФИГУРАЦИИ ПЛАНЕТ Цель работы: Изучение закономерностей в движении планет и вычисление их конфигураций. Оборудование: Астрономический календарь – постоянная часть или справочник любителя астрономии, калькулятор, подвижная карта звездного неба. Вопросы к допуску: 1. Формулировка законов Кеплера 2. Конфигурации планет. 3. Звездный период обращения Юпитера вокруг Солнца Т = 12 лет. Каково среднее расстояние от Юпитера до Солнца? Основные теоретические сведения: Движение планет вокруг Солнца описывается законами Кеплера, которые формулируются так: 1 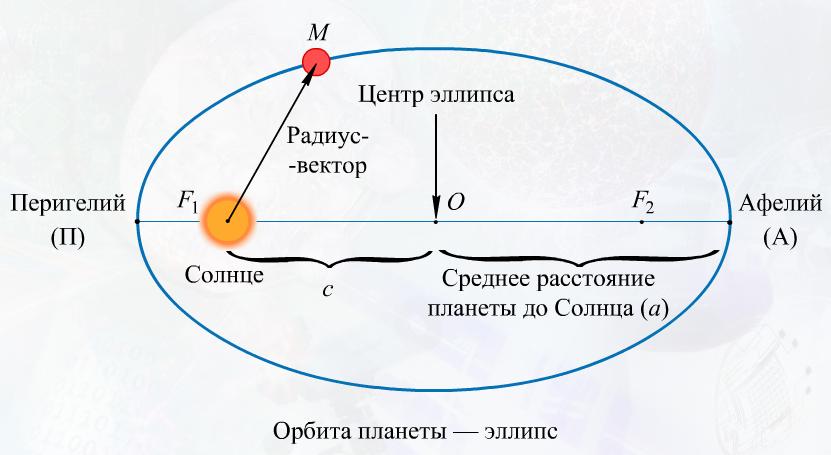 . Все планеты движутся по эллипсам, в одном из фокусов которых (общем для всех планет) находится Солнце.2. Радиус - вектор планеты в равные промежутки времени описывает равновеликие площади. 3. Квадраты сидерических периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их эллиптических орбит. 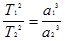 где Т1, Т2 - сидерические периоды обращений планет, а1, а2 - большие полуоси их орбит. Эта формулировка подходит для описания движения всех небесных тел: спутников, комет, двойных звёзд и др. 2. Площадь, описанная радиусом вектором за единицу времени есть величина постоянная. 3. 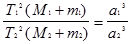 где M и m - массы центрального тела и спутника, индексы 1 и 2 относятся к различным парам “тело-спутник”. Прямые и попятные движения планет объясняются различием орбитальных линейных скоростей планеты и Земли. Синодический период обращения (S) планеты - промежуток времени между её двумя последовательными одноименными конфигурациями. Сидерический или звёздный период обращения (Т) - промежуток времени, в течение которого планета совершает один полный оборот вокруг Солнца по своей орбите. Сидерический период обращения Земли называется звёздным годом (Тз). Угловое перемещение по орбите за сутки у планеты = 360/Т, а у Земли = 360/Тз. разность суточных угловых перемещений планеты и Земли есть видимое смещение планеты за сутки, т.е. 360/S. Получаем для нижних планет:  Для верхних планет:  Это уравнения синодического движения. Непосредственно из наблюдений могут быть определены только синодические периоды обращений планет S и сидерический период обращения Земли. Сидерические же периоды обращений планет вычисляются по уравнению синодического движения. Продолжительность звёздного года равна 365,256 средних солнечных суток. 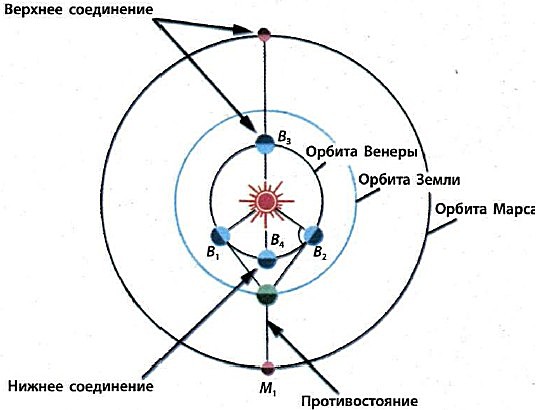 Взаимное расположение планет легко устанавливается по их гелиоцентрическим эклиптическим координатам, значения которых на различные дни года публикуются в астрономических календарях - ежегодниках, в таблице под названием “Гелиоцентрические долготы планет”. Центром этой системы координат является центр Солнца, а основным кругом - эклиптика.Большие круги, проведённые через полюсы эклиптики, называются кругами эклиптических широт, и по ним отсчитывается от эклиптики гелиоцентрическая широта b, которая считается положительной в северном эклиптическом полушарии и отрицательной - в южном эклиптическом полушарии небесной сферы. Гелиоцентрическая долгота l отсчитывается по эклиптике от точки весеннего равноденствия против часовой стрелки до основания круга широты светила и имеет значения в пределах от 0 до 3600. Из-за малого наклонения орбит больших планет к плоскости эклиптики эти планеты всегда находятся вблизи эклиптики, и в первом приближении можно считать их гелиоцентрическую широту b = 0. Тогда положение планеты относительно Солнца определяется лишь одной её гелиоцентрической долготой. Если периоды обращения любых двух планет, например Земли и Марса, обозначить через Тз и Тм , а их средние расстояния от Солнца – аз и ам, то третий закон Кеплера можно записать в виде равенства: Т2м / Т2з = а3м / а3з. Но ведь период обращения Земли вокруг Солнца равен одному году (Тз = 1), а среднее расстояние Земля – Солнце принято за одну астрономическую единицу (аз = 1 а.е.). Тогда данное равенство примет более простой вид: Т2м – а3м Период обращения планеты (в нашем примере Марса) можно определить из наблюдений. Он составляет 687 земных суток, или 1,881 года. Зная это, нетрудно вычислить среднее расстояние планеты от Солнца в астрономических единицах:  Т.е. Марс находится в среднем в 1,524 раза дальше от Солнца, чем наша Земля. Следовательно, если известно время обращения какой-нибудь планеты, то по нему можно найти её среднее расстояние от Солнца. Таким путём Кеплеру удалось определить расстояния всех известных в ту пору планет: Меркурий – 0,39, Венера – 0,72, Земля – 1,00, Марс – 1,52, Юпитер – 5,20, Сатурн – 9,54. | |||||||||||||||||||||||||||||||||||