ЖБК 200 вопросов и ответов. Бетон, арматура и железобетон
 Скачать 11.86 Mb. Скачать 11.86 Mb.
|
77. КАК УПРОЩЕННО ПРОВЕРИТЬ ПРОЧНОСТЬ НОРМАЛЬНОГО СЕЧЕНИЯ?Если задаться плечом внутренней пары сил (например, zb = 0,8ho для прямоугольного и zb = ho – 0,5 hf для таврового сечений), тогда прочность можно проверить по простой формуле Мu = RsAszb, а преобразовав формулу, можно подобрать и арматуру Аs = M/(Rszb). Но упрощение это очень грубое, оно может дать ошибку до 15...20 % и пользоваться им можно только для первой прикидки. 78. КАК ВЛИЯЕТ ПРОЧНОСТЬ БЕТОНА НА ПРОЧНОСТЬ НОРМАЛЬНОГО СЕЧЕНИЯ?В 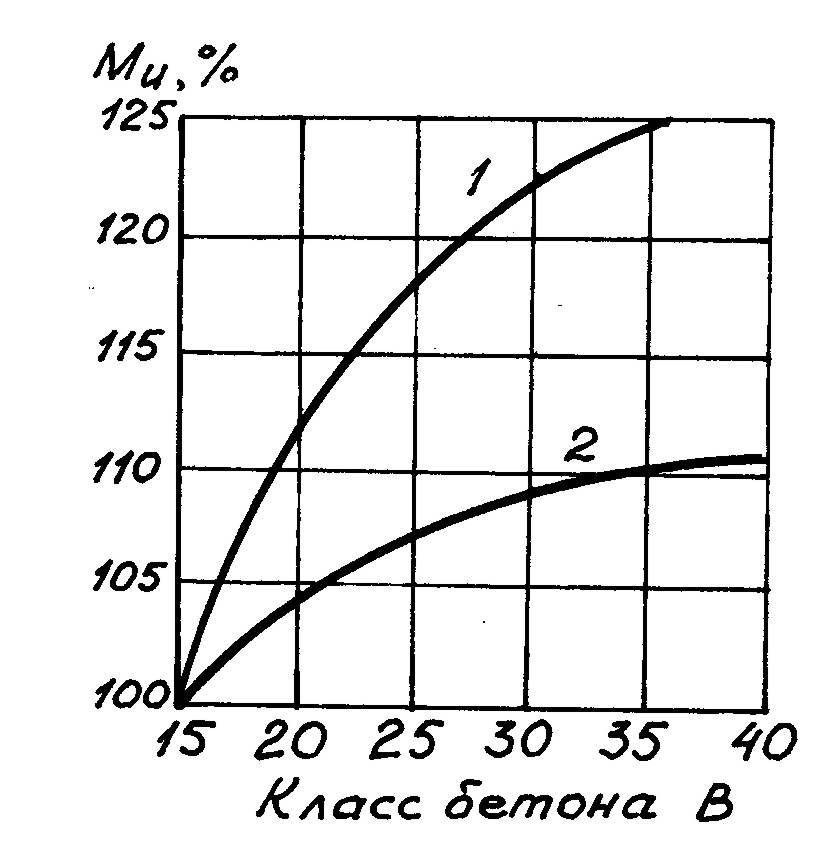 лияет не столь существенно, как кажется на первый взгляд. Например, если взять прямоугольное нормально армированное сечение (т.е. с относительной высотой сжатой зоны = R) из бетона класса В15, то повышение прочности бетона вдвое (до В30) увеличивает прочность сечения Mu всего на 22,5 % (кривая 1 на рис.37).Еще более низкий эффект – при слабом армировании: в аналогичной балке при = 0,5R повышение класса бетона с В15 до В30 увеличивает Mu всего на 9,2 % (кривая 2). Низкая эффективность объясняется тем, что при сохранении армирования неизменным с увеличением прочности Rb пропорционально уменьшается высота сжатой зоны х. Это приводит к увеличению плеча внутренней пары (zb = h0 – 0,5х), которое, однако, растет намного медленнее, чем уменьшается х. Столь же неэффективно увеличение Rb в тавровых сечениях с полкой в сжатой зоне, большинство которых относится к слабо армированным с 0,5R. Поэтому более целесообразно повышать прочность сечения за счет увеличения армирования, и только в крайнем случае следует повысить Rb. 79. ПОЧЕМУ В ПРЕДНАПРЯЖЕННЫХ изгибаемых элементах обычно ПРИМЕНЯЮТ БЕТОН БОЛЕЕ ВЫСОКИХ КЛАССОВ, ЧЕМ В в элементах без преднапряжения?Это вызвано, главным образом, необходимостью либо обеспечить требуемую прочность сечений при обжатии, либо уменьшить потери напряжений в напрягаемой арматуре. В связи с этим приходится повышать передаточную прочность бетона Rbp, а вместе с ней – и класс бетона (см. также вопрос 41). 80. КАК РАССЧИТЫВАЮТ СЕЧЕНИЯ С МНОГОРЯДНЫМ РАСПОЛОЖЕНИЕМ АРМАТУРЫ?Чем ближе арматура находится к нейтральной оси, тем меньше в ней деформации s и напряженияs. Согласно гипотезе плоских сечений, s растут пропорционально удалению от нейтральной оси (рис. 38,а). Если бы так же пропорционально росли напряжения s, то задача была бы достаточно простой. Однако такое возможно только в переармированных сечениях, да и то при условии, что напряжения в крайнем ряду растянутой арматуры не превышают предела пропорциональности (примерно 80 % предела текучести), когда работа стали соответствует закону Гука. Уже для нормально армированных сечений такой подход дает заметную неточность результата, и совершенно недопустимую – для слабо армированных сечений. В таких сечениях арматура крайнего ряда ведет себя совсем иначе (см. вопрос 62). “Мягкая” сталь течет, напряжения в ней не растут после достижения Rs, но зато растут напряжения в следующих рядах, причем в соседних они тоже могут достичь предела текучести. “Твердая” сталь работает за условным пределом текучести, напряжения в ней s = s6Rs; в зависимости от высоты сжатой зоны напряжения в соседнем ряду тоже могут достичь или даже превысить Rs. 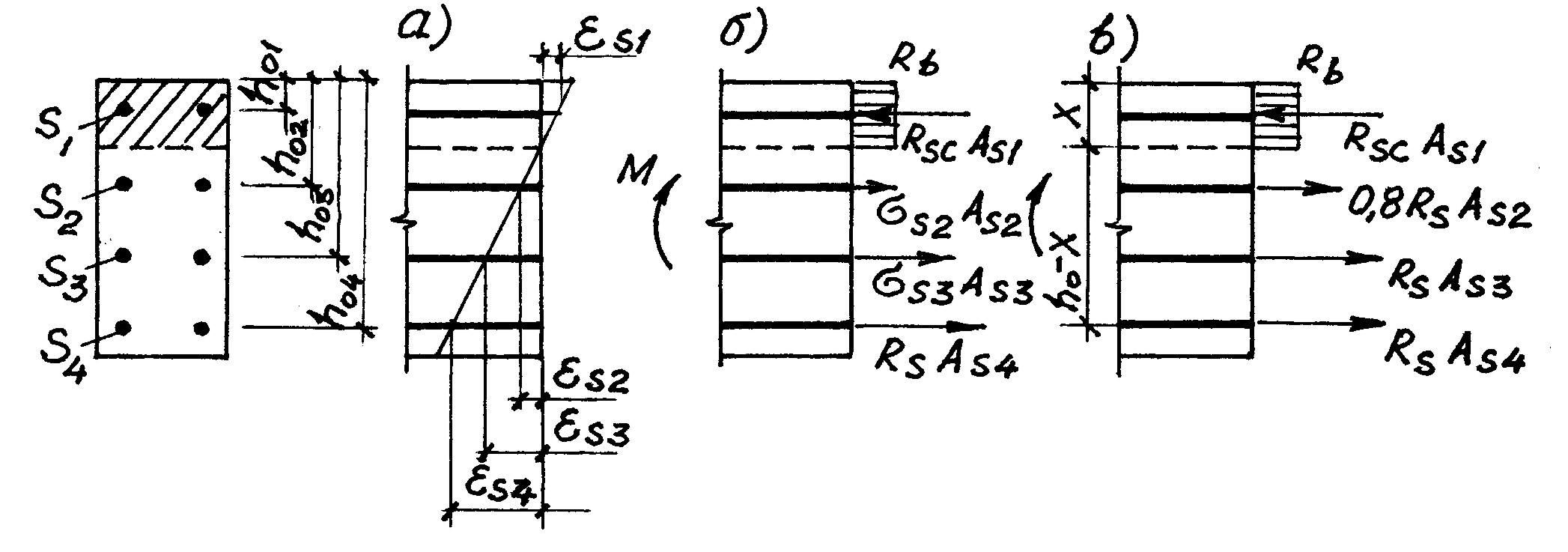 Рис. 38 Из приведенного видно, что задача достаточна сложна: кроме высоты сжатой зоны, неизвестными являются напряжения во всех рядах арматуры, исключая крайний сжатый (там sc=Rsc). Решение задачи дается в Нормах проектирования в “общем случае” расчета, подразумевающем решение системы уравнений; имеются и другие методы с использованием ЭВМ. Расчет сечений, армированных “мягкой” сталью, можно существенно упростить, допуская небольшую погрешность: вся арматура, расположенная в нижней половине растянутой зоны(ho x),вводится в расчет с напряжением s = Rs, а расположенная в верхней половине с напряжением s = 0,8Rs (рис.38,в). |
