ЖБК 200 вопросов и ответов. Бетон, арматура и железобетон

• Название: Бетон, арматура и железобетон
• Анкор: ЖБК 200 вопросов и ответов.doc
• Дата: 07.02.2017
• Размер: 11.86 Mb.
• Имя файла: ЖБК 200 вопросов и ответов.doc
• Тип: Документы; #2374
• страница: 22 из 53

81. ДЛЯ ЧЕГО ВЫПОЛНЯЮТ РАСЧЕТ ПРОЧНОСТИ НОРМАЛЬНЫХ СЕЧЕНИЙ В СТАДИИ ОБЖАТИЯ, ТРАНСПОРТИРОВКИ И ВОЗВЕДЕНИЯ КОНСТРУКЦИЙ?

В этой стадии конструкции работают, как правило, по иной расчетной схеме, чем при эксплуатации, а сечения на отдельных участках испытывают изгибающие моменты противоположного знака. К тому же, бетон еще не успел набрать проектную прочность, а у преднапряженных элементов проявились только первые потери напряжений в арматуре, т.е. сила обжатия (Р₁)больше, чем при эксплуатации (Р₂). Например, при подъеме преднапряженной балки к отрицательному изгибающему моменту М_р от силы обжатия Р добавляется отрицательный момент М_wот собственного веса q_w (рис.39). Верхняя арматура вместо сжатия испытывает растяжение, площадь ее сечения может оказаться недостаточной и произойдет разрушение по нормальному сечению.

82. КАКОВЫ ОСОБЕННОСТИ РАСЧЕТА ПРОЧНОСТИ НОРМАЛЬ­НЫХ СЕЧЕНИЙ В СТАДИИ ОБЖАТИЯ, ТРАНСПОРТИРОВКИ И ВОЗВЕДЕНИЯ КОНСТРУКЦИЙ?

О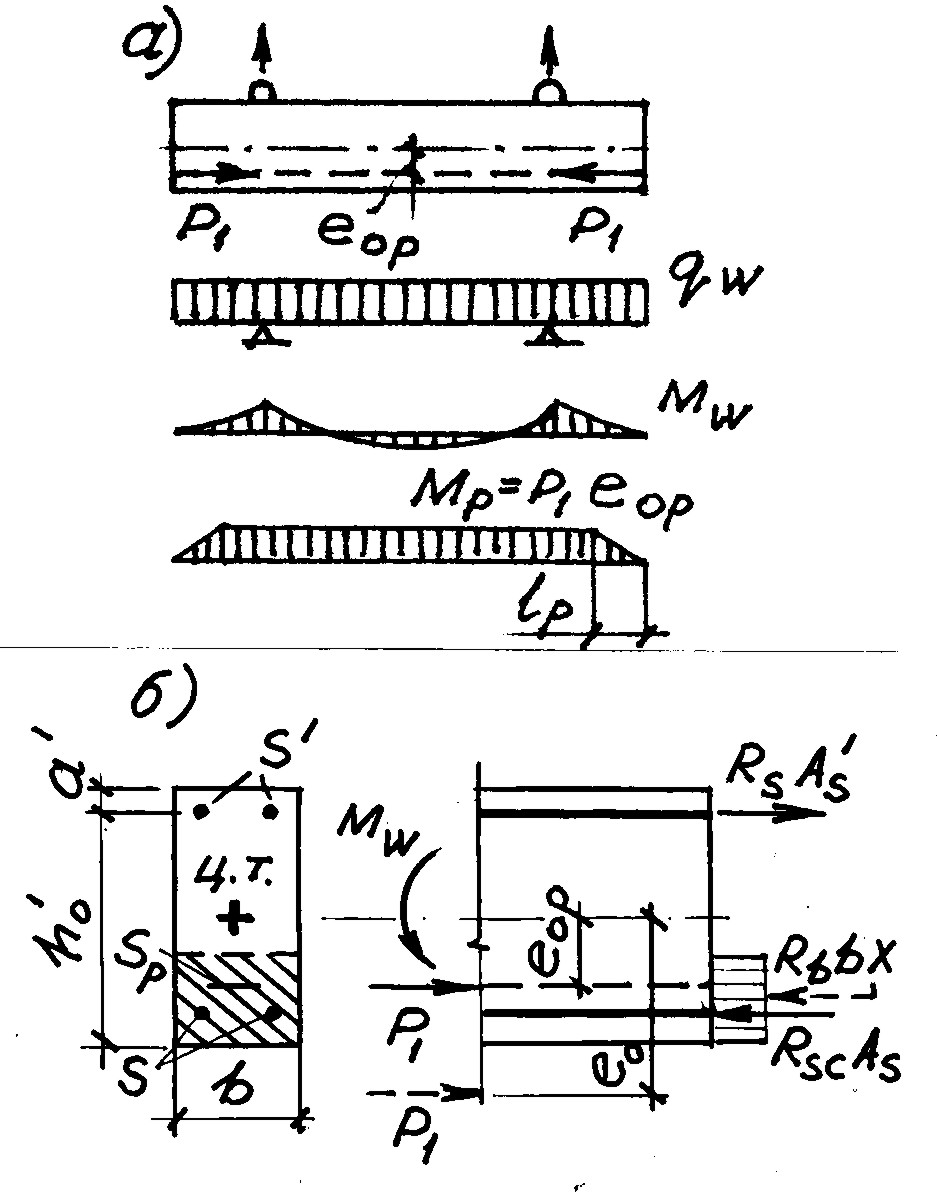


Рис. 39
собенности заключаются в следующем (рис. 39,б). Сила обжатия Р₁ рассматривается как внешняя нагрузка: Р₁ = (_sp1330)А_sp, где _sp1  величина преднапряжения арматуры с учетом только первых потерь и с учетом коэффициента точности натяжения _sp > 1; 330(МПа)  величина падения напряжений в арматуре S_p в момент разрушения сжатой зоны, соответствующая предельной сжимаемости бетона _bu при кратковременном сжатии (потому она и меньше обычно принимаемых величин 400 и 500 МПа, см. вопрос 27). С учетом кратковременного характера нагрузки и передаточная прочность бетона R_bp умножается на коэффициент _b2 = 1,1. Вместе с тем нагрузка от собственного веса не только принимается расчетной, но и умножается на коэффициент динамичности К_д = 1,4 (при перевозке изделий К_д = 1,6), который учитывает дополнительную перегрузку от толчков, рывков, подбрасываний и т.п. воздействий.

В итоге, расчет сводится к расчету нормального сечения на внецентренное сжатие от действия силы Р₁, приложенной относительно оси с эксцентриситетом е_о = е_ор + М_w /P₁ (см. главу 4). При отсутствии предварительного напряжения (Р = 0) сечение рассчитывают на обычный поперечный изгиб, лишь поменяв в расчете местами арматуру S и S.

3.2. наклонные сечения

83. КАК ПРОИСХОДИТ РАЗРУШЕНИЕ НАКЛОННЫХ СЕЧЕНИЙ?

Разрушение происходит по одной из трех схем.

1. Раздавливание тонкой стенки (ребра) по наклонной полосе между трещинами от действия главных сжимающих напряжений _mc (рис. 40,а). Чем выше прочность бетона R_b и чем больше толщина стенки b, тем лучше стенка сопротивляется действию _mc (при этом R_b повышается с увеличением интенсивности поперечного армирования, играющего для бетона роль обоймы, аналогичную сеткам косвенного армирования). Увеличение рабочей высоты сечения h_o уменьшает касательные напряжения _xy, а вместе с ними  и _mc.

Прочность наклонной полосы проверяют по эмпирической формуле: Q 0,3_w1_b1R_bbh_o, где _w1 и _b1  коэффициенты, учитывающие интенсивность поперечного армирования и вид бетона, Q  максимальная величина поперечной силы (как правило, это опорная реакция). Требования к прочности наклонной полосы являются главной причиной, почему у тавровых и двутавровых балок с тонкой стенкой устраивают уширения на опорах.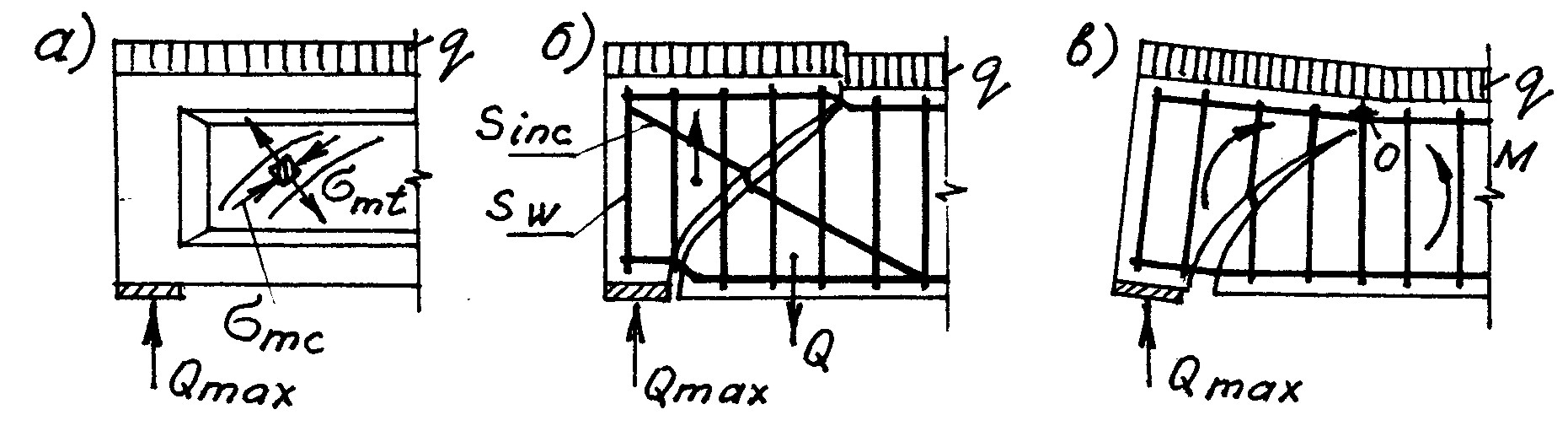

Рис. 40
2. Взаимный сдвиг двух частей изгибаемого элемента, разделенных наклонной трещиной (рис. 40,б). Сдвиг вызывается поперечной силой Q, а сопротивляется ей поперечная S_w, отогнутая S_inc арматура и бетон сжатой зоны, работающий на срез. При такой схеме наклонное сечение рассчитывают на действие поперечной силы, а условие прочности записывают в виде: Q  Q_u, где Q – поперечная сила от внешней нагрузки, находящейся по одну сторону от наклонного сечения, Q_u – несущая способность наклонного сечения. Из рис. 40,б видно, что сдвигу сопротивляется и продольная арматура, работающая на срез и изгиб (в ней возникают т.н. «нагельные» усилия), однако в расчетах ее, как правило, не учитывают.

3. Взаимный поворот относительно точки О двух частей изгибаемого элемента, разделенных наклонной трещиной (рис. 40,в), который вызывается действием изгибающего момента М. Ему сопротивляется продольная S, поперечная S_w и отогнутая S_incарматура, а условие прочности записывают в виде: М  М_u. Точка поворота О находится в точке приложения равнодействующей усилий в сжатой зоне.