Билет18. Билет 18 Ряд Фурье для функций с произвольным периодом. Условия разложимости
 Скачать 289.5 Kb. Скачать 289.5 Kb.
|
|
Билет №18 1. Ряд Фурье для функций с произвольным периодом. Условия разложимости. Тригонометрический ряд периодической функции f(x) с периодом 2 называется рядом Фурье коэффициенты определяются по формулам Функция может быть задана не только на отрезке длиной 2π, но также на отрезке любой длины 2l. Тогда функция разложима в ряд Фурье следующего вида: причем коэффициенты ряда вычисляются по формулам Разлагать в ряд Фурье можно и периодические функции с периодом, отличным от 2 Пусть функция f(x), определенная на отрезке [-l,l], имеет период 2 Сделав подстановку Действительно, если t = - имеем -l<х<l; т.е. Разложение функции (t) в ряд Фурье на отрезке [— где 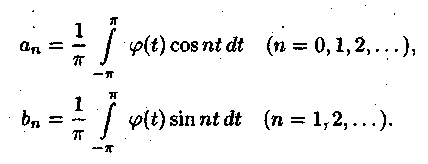 • - • - Возвращаясь к переменной x и заметив, что 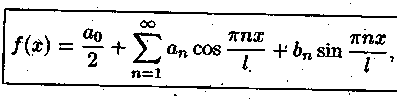 (1) (1)где 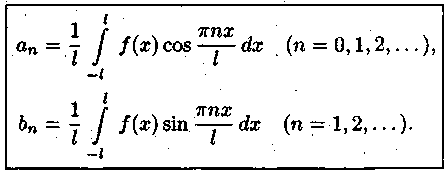 (2) (2)Ряд (1) с коэффициентами, вычисляемыми по формулам (2), называется рядом Фурье для функции f(x) с периодом Т = 2l. Замечание. Все теоремы, имеющие место для рядов Фурье 2 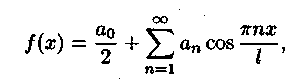 (3) (3)где • если f(x) — нечетная функция, то 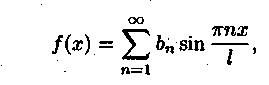 (5) (5)где 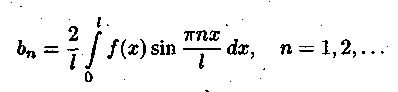 (6) (6)2. Найти градиент функции Градиент функции Найдем частные производные: 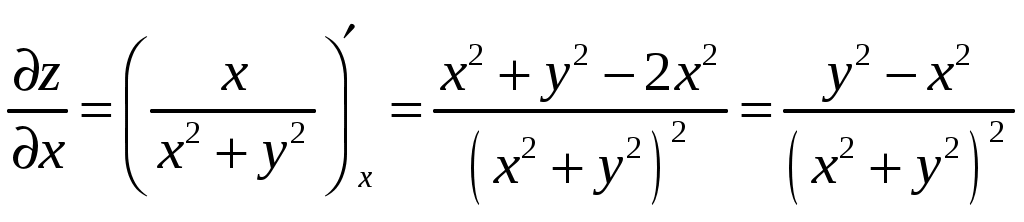 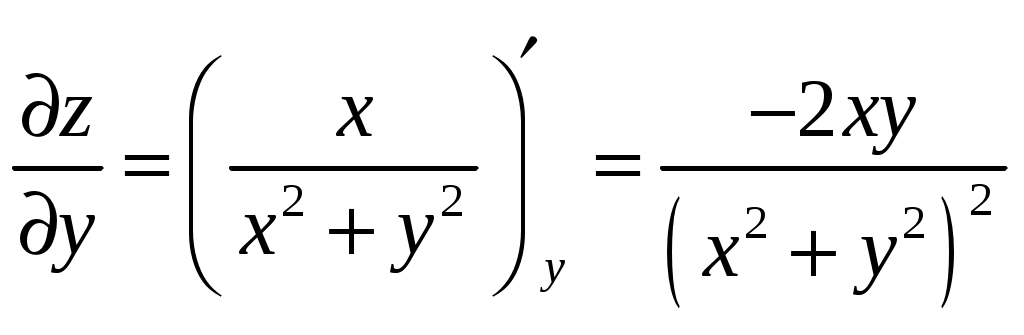 и их значения в точке М(1,1) 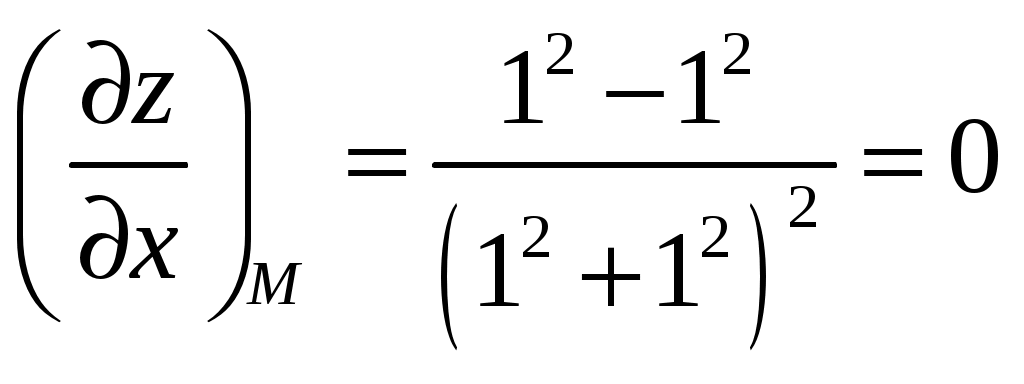 , ,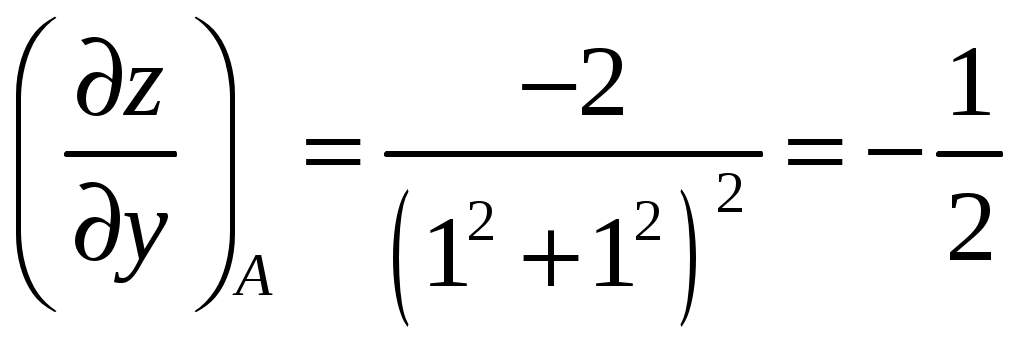 . .Тогда градиент в точке М равен: 3. Изменить порядок интегрирования. Область интегрирования изобразить на чертеже. Строим область интегрирования G по пределам интегрирования: Справа область G ограничена кривой 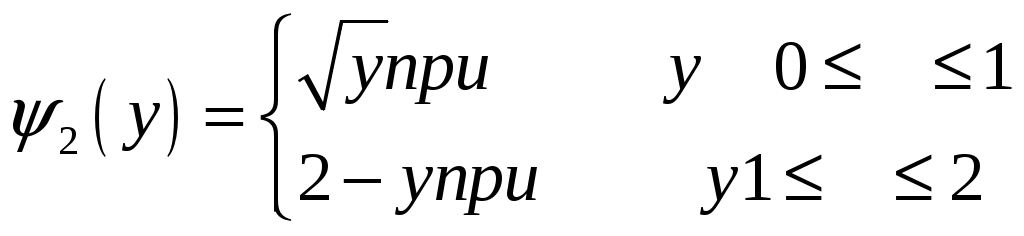 А слева – прямой х=0. Поэтому имеем: 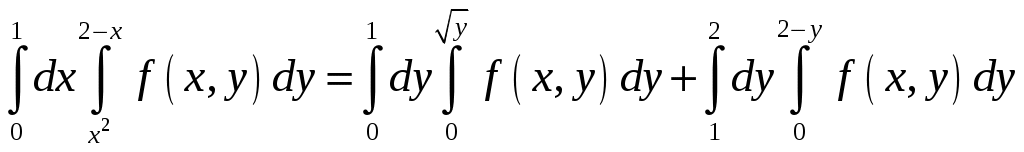 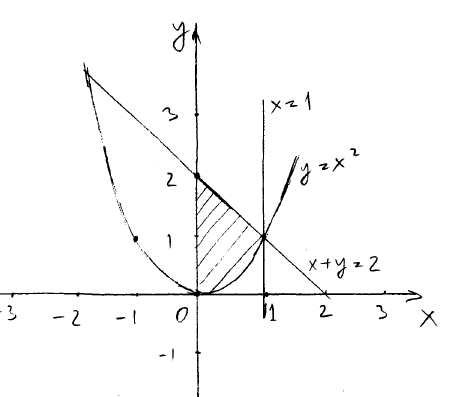 4. Определить область сходимости ряда. Составим ряд из абсолютных величин членов данного ряда: 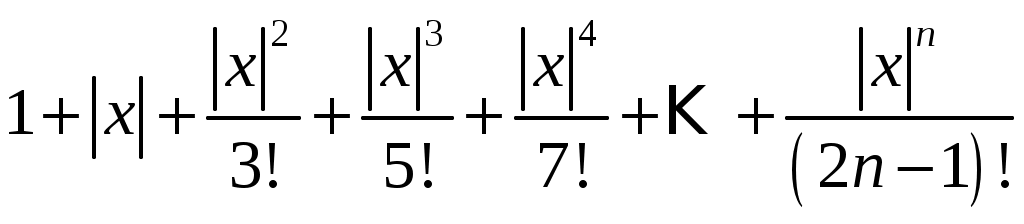 Согласно признаку Даламбера ряд сходится при тех значениях х, для которых: 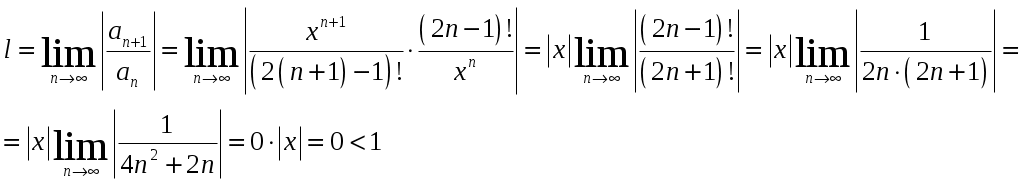 . .Следовательно, при любом конечном х по признаку Даламбера данный ряд абсолютно сходится. Область сходимости данного ряда вся числовая ось. 5. Найти решение дифференциального уравнения Данное уравнение является линейным дифференциальным уравнением первого порядка Положим Подставляя эти выражения в исходное уравнение, получим: Выберем Уравнение (1) при Интегрируем по частям. Полагаем 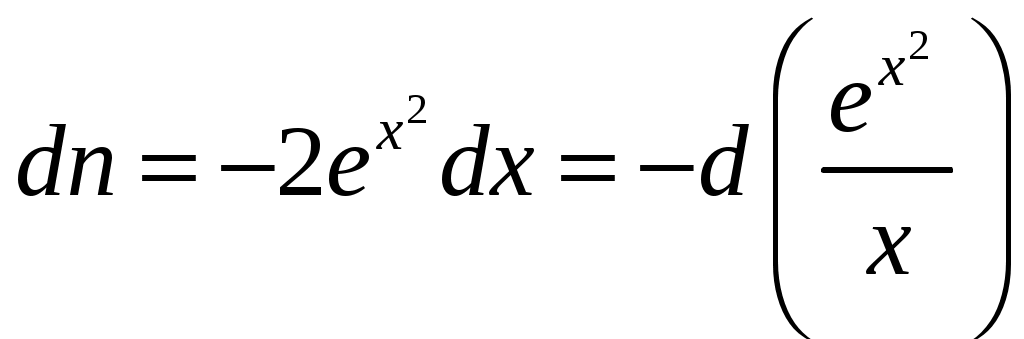 , ,Тогда Тогда Следовательно, При заданных начальных условиях х=1, Искомое частное решение имеет вид: 7. Найти частное решение дифференциального уравнения Общий вид уравнения Характеристическое уравнение Частное решение ищем в виде Подставим полученные выражения в исходное уравнение: 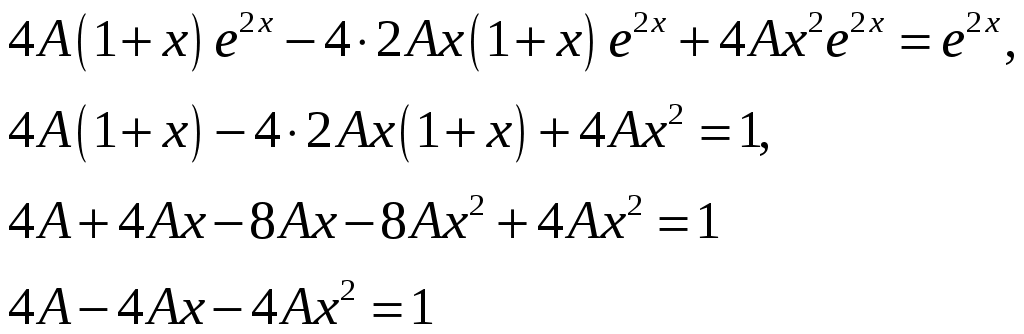 Откуда 4А=1, Следовательно, Следовательно, общее решение уравнения Для нахождения искомого частного решения воспользуемся заданными начальными условиями. Найдем производную общего решения: Подставив в выражения для общего решения и его производной значения х=0, y=0 и 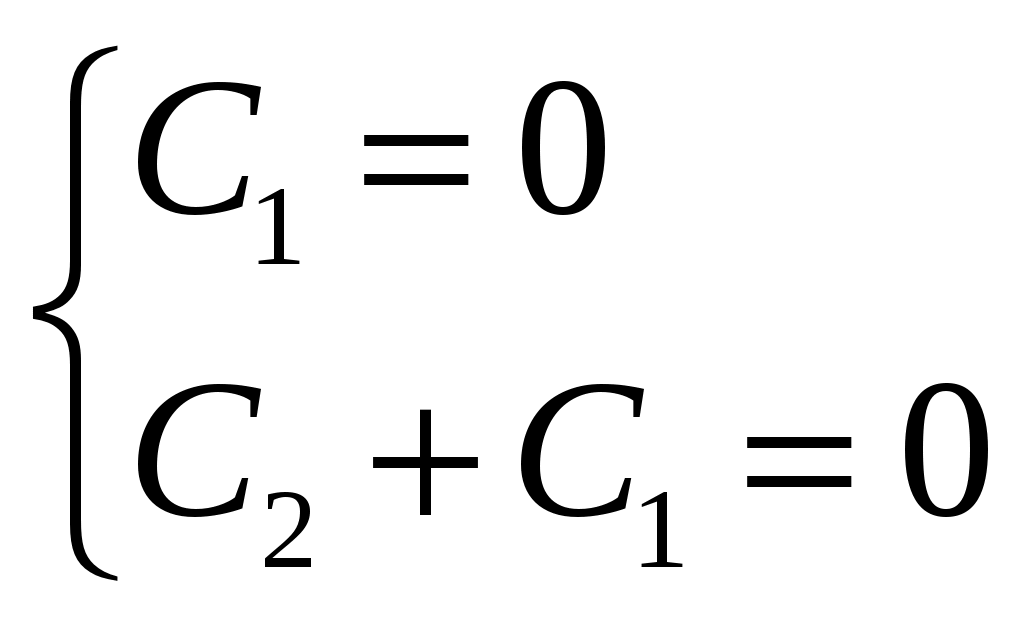 Отсюда Искомое частное решение имеет вид: |
