Лекции Гармонический анализ. Гармонический анализ
 Скачать 1.04 Mb. Скачать 1.04 Mb.
|
|
ГАРМОНИЧЕСКИЙ АНАЛИЗ Введение. Современное развитие техники предъявляет повышенные требования к математической подготовке инженеров. В результате постановки и исследования ряда конкретных проблем механики и физики возникла теория тригонометрических рядов. Важнейшую роль ряды Фурье играют во всех областях техники, опирающихся на теорию колебаний и теорию спектрального анализа. Например, в системах передачи данных для описания сигналов практическое применение спектральных представлений неизменно приводит к необходимости экспериментального осуществления разложения Фурье. Особенно велика роль тригонометрических рядов в электротехнике при изучении периодических несинусоидальных токов: амплитудный спектр функции находится с помощью ряда Фурье в комплексной форме. Для представления непериодических процессов применяется интеграл Фурье. Тригонометрические ряды находят важное применение в многочисленных разделах математики и доставляют особенно удобные методы для решения трудных задач математической физики, например, задачи о колебании струны и задачи о распространении тепла в стержне. §1. Периодические функции. Многие задачи науки и техники связаны с периодическими функциями, отражающими циклические процессы. Определение 1. Периодическими называются явления, повторяющиеся в одной и той же последовательности и в одном и том же виде через определенные интервалы аргумента. Пример. В спектральном анализе – спектры. Определение 2. Функция у = f(x) называется периодической с периодом Т, если f(x + Т) = f(x) при всех х и x + Т из области определения функции. Н 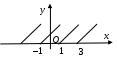 а рисунке период изображенной функции Т = 2. а рисунке период изображенной функции Т = 2.Определение 3. Наименьший положительный период функции называется основным периодом. Там, где приходится иметь дело с периодическими явлениями, почти всегда встречаются тригонометрические функции. Период функций Период тригонометрических функций с аргументом (ах) находится по формуле: Пример. Найти основной период функций 1) Решение. 1) 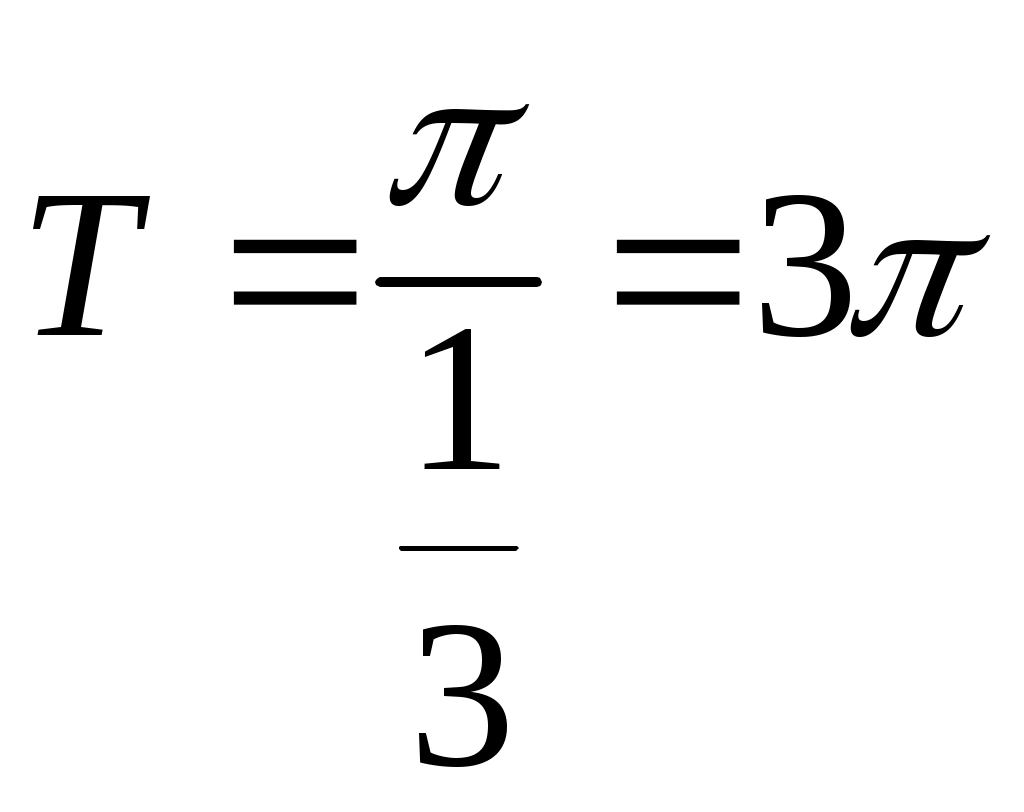 . .Лемма. Если f(x) имеет период Т, то интеграл этой функции, взятый в пределах, отличающихся на Т, не зависит от выбора нижнего предела интегрирования, т.е. Основной период сложной периодической функции у = f(x) (состоящей из суммы периодических функций) – это наименьшее общее кратное периодов составляющих функций. То есть, если f(x) = f1(x) + f2(x), Т1 – период функции f1(x), Т2 – период функции f2(x), то наименьший положительный период Т должен удовлетворять условию: T = nT1 + kT2, где основной период сложной периодической функции – наименьшее общее кратное чисел T1 и T2. Пример. Найти наименьший положительный (или основной) период функции Решение. Пусть f1(x) = Примеры из ФЭПО. Пример 1. Указать периодические функции с периодом 2 из представленных ниже: 1) Решение. Пример 2. Наименьший положительный период функции Варианты ответов 1) Решение. Пример 3. Наименьший положительный период функции Решение. Пример 4. Какая из указанных функций 1) Решение. Пример 5. Для периодической функции у = f(x) с периодом Т = 5 выполняется равенство: 1) f(x + 5) = f(x), 2) f(5x) = f(x), 3) f(x + §2. Гармонические колебания. Определение 4. Простым гармоническим колебанием называется простейшее периодическое явление, в котором расстояние Sколеблющейся точки от положения равновесия является функцией времени t: S = Asin(t + 0), где A – амплитуда колебания, – круговая частота; t – время; 0 –начальная фаза ( при t = 0); (t + 0) – фаза колебания; Т = 2/– период колебаний. Определение 5. График простого гармонического колебания, описываемого уравнением S = Asin(t+0), называется простой гармоникой. Пример. Уравнение гармонического колебания имеет вид S = 3sin(2t + Определение 6. Колебания, получающиеся в результате наложения нескольких простых гармонических колебаний, называется сложными гармоническими колебаниями, а их графики сложными гармониками. Например, в случае наложения двух простых гармонических колебаний, получаем: S = A1sin(1t + 1) + A2sin(2t+ 2 ). Если 1 = 2 , то результирующее колебание будет снова простым гармоническим колебанием с той же частотой и тем же периодом. Пусть 1≠ 2 . Периоды простых колебаний равны Сложное колебание S = A1sin(r1t + 1) + A2sin(r2t+ 2) будет периодическим с периодом Т = 2/. Пусть Пусть = 1, тогда Т = 2. К этому всегда можно прийти, изменив масштаб по оси t, т.е. положив t = t /. Суммы простых колебаний( = 1) Примеры из ФЭПО Пример 1. Гармоническое колебание с амплитудой А, частотой и начальной фазой описывается законом… Варианты ответов: 1) Решение. Пример 2. Гармоническое колебание общего вида с начальной фазой Решение. Пример 3. Определить абсолютную величину сдвига по фазе между гармониками Решение. Пример 4. Амплитуда гармонического колебания равна 0,07. За 2 минуты совершается 240 колебаний. Начальная фаза колебаний равна Решение. Уравнение гармонического колебания имеет вид 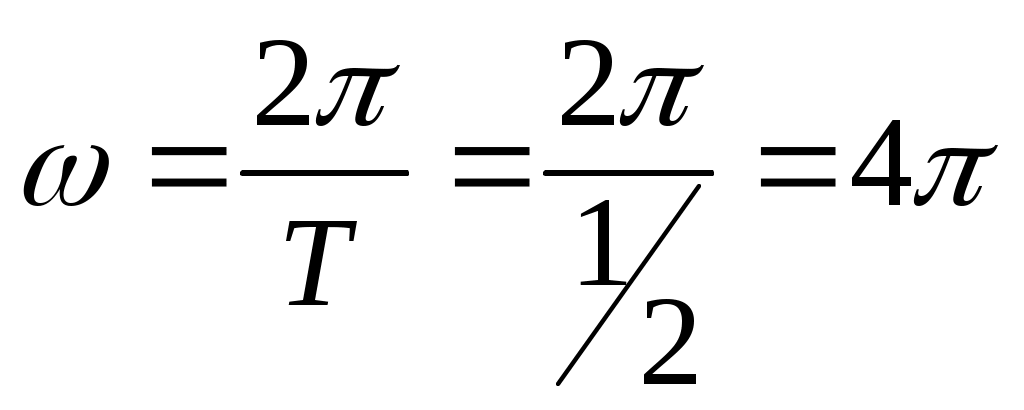 . Следовательно, уравнение гармонического колебания имеет вид . Следовательно, уравнение гармонического колебания имеет вид Пример 5. Функция Решение. 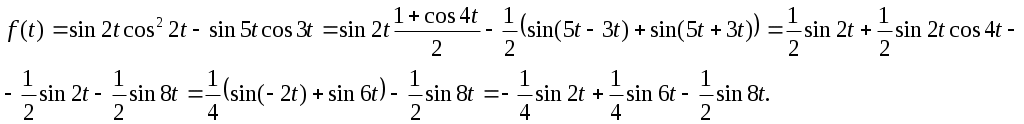 Выше было показано, что наложение простых гармонических колебаний создает разнообразие периодических движений, отнюдь не похожих на простые гармонические колебания. Подобрать простые гармонические колебания так, чтобы их наложение вызвало заранее данное периодическое движение, то есть представить всякое периодическое движение как сложное гармоническое колебание, можно, если привлечь к рассмотрению бесконечные суммы простых гармоник, а именно ряды. Удобнее рассматривать представление периодических функций в виде тригонометрического ряда или его частичной суммы с достаточной степенью точности. Следовательно, если требуется разложить на простые гармоники функцию с периодом 2π, необходимо, чтобы каждая из этих простых функций имела 2π в качестве одного из своих периодов, т.е. необходимо, чтобы ω = n, где n – целое. Это означает, ч то в качестве составляющих следует брать гармоники с целыми частотами. Для решения ряда практических задач обычно требуется разложить сложную периодическую функцию периода Т на простые периодические функции вида (acosωx+bsinωx), имеющие период § 3. Тригонометрические ряды. Ряды Фурье. Основные понятия. Разложение в ряд Фурье функций с периодом 2. Определение 7. Функциональный ряд вида: называется тригонометрическим, причем an и bn – действительные числа, не зависящие от x. Пусть y= f(x) – произвольная периодическая функция с периодом Т = 2, следовательно, функцию можно рассматривать в любом интервале длины 2, например, (–; ). На других участках оси (Ох) функция f(x) и ее разложение в ряд будет повторять свои значения и свое поведение в основном интервале. Предположим, что для любого x(–; ) периодическая функция оказалась такой, что для нее нашлось разложение в равномерно сходящийся ряд указанного вида: f(x) = Такое представление дает возможность находить численные значения функции, устанавливать различные свойства функций, решать дифференциальные уравнения и т.п. Получим формулы для вычисления коэффициентов ak и bk. Проинтегрируем почленно данное равенство в пределах от – π до π (законное в силу предложенной сходимости): Вычислим отдельно следующие интегралы: если n– целое, 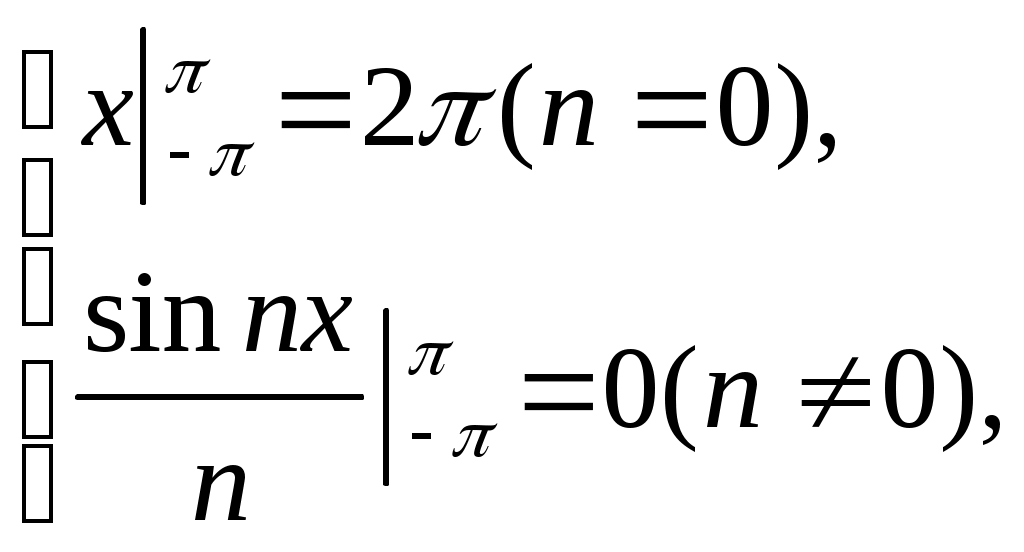 (1.3) (1.3)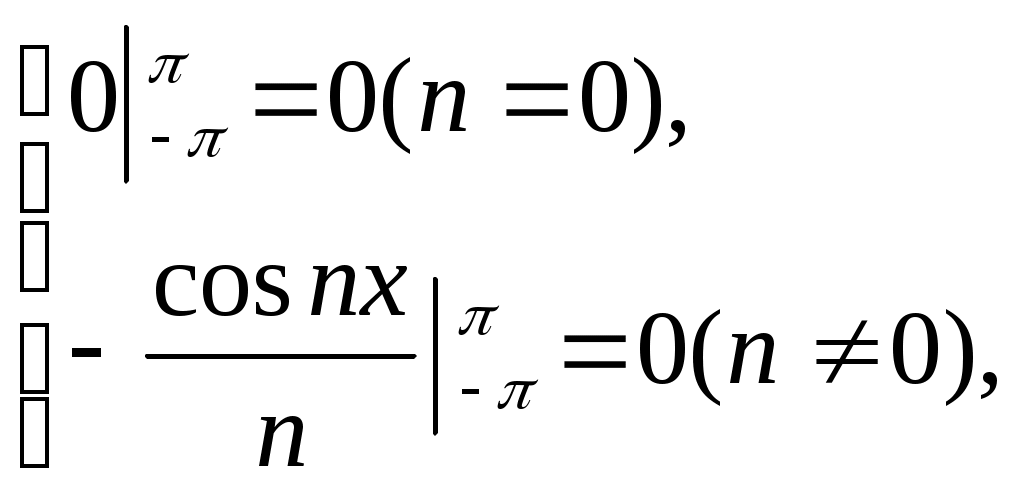 (1.4) (1.4) если n, m – целые, положительные 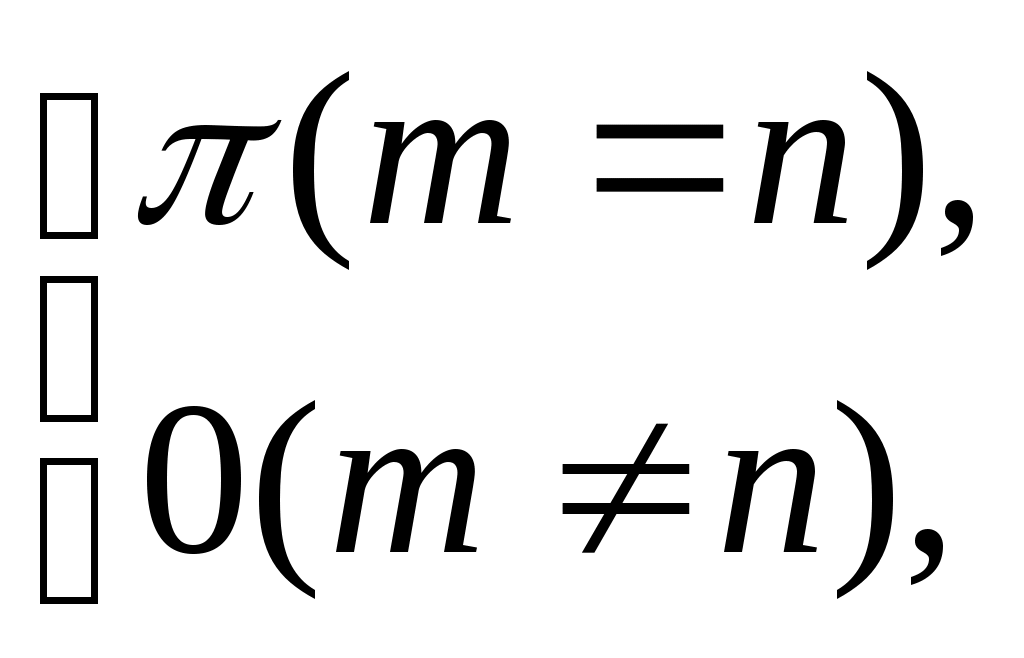 (1.5) (1.5)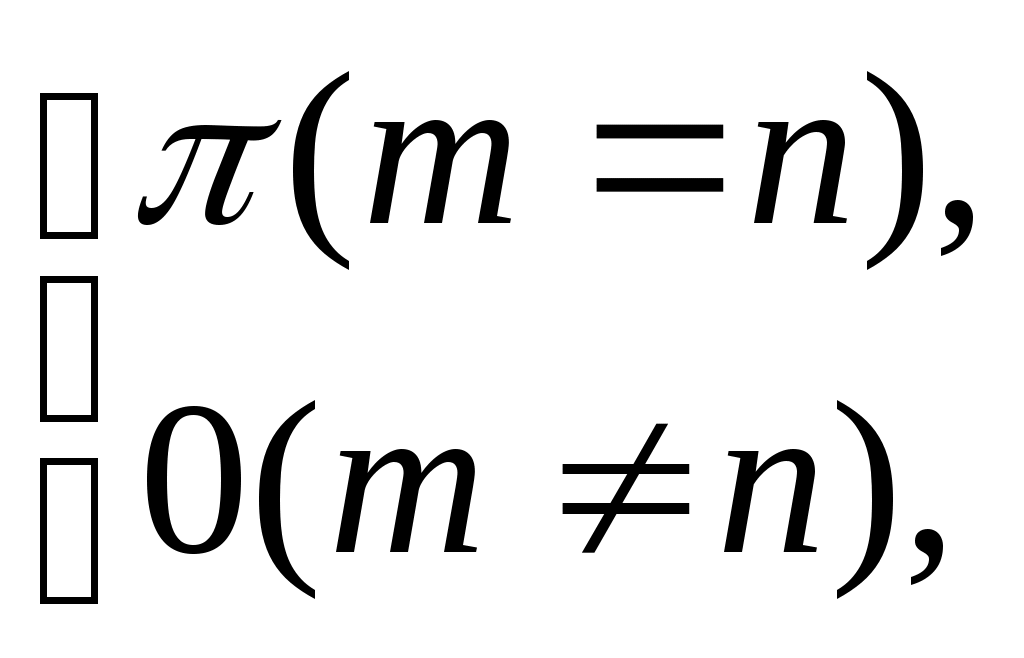 (1.6) (1.6)С учетом формул (1.3) и (1.4) почленное интегрирование равенства (1.2) дает: Умножая (1.1) на cos nx и интегрируя почленно от – π до π, с учетом (1.3), (1.5), (1.7), получим: Аналогично, умножая (1.1) на sin nx и интегрируя почленно от – π до π и учитывая (1.4), (1.6), (1.7), получим: Таким образом, из равенств (1.8), (1.9), (1.10) получим выражения для нахождения коэффициентов. Теорема 1. Если функция f(x), заданная и непрерывная на отрезке [-; ], разлагается в тригонометрический ряд, то коэффициенты его определяются единственным образом. Определение 8. Пусть f(x) – произвольная функция с периодом 2, заданная в интервале (–; ). Пусть существует интеграл от данной функции в интервале (–; ), при этом f(x) может иметь конечное число точек разрыва 1-го рода. Рядом Фурье этой функции называется ряд коэффициенты которого определяются по формулам: а0 = аn= bn = Замечание 1. Для вычисления интегралов потребуются следующие формулы: Из определения ряда Фурье не следует, что функция должна в него разлагаться. Из сказанного выше следует следующая теорема: Теорема 2 (единственности). Если непрерывная на [-; ] функция разлагается в равномерно сходящийся тригонометрический ряд, то этот ряд будет обязательно ее рядом Фурье. Замечание 2. Исходя из теоремы, в определении можно рассматривать не интервал (–; ), а отрезок [–; ]. Функция f(x) не всегда разлагается в свой ряд Фурье, т.е. является его сумой, даже если он сходится, а лишь тогда, когда она удовлетворяет условиям основной теоремы: Теорема 3 (основная). Если функция f(x) кусочно-гладкая на отрезке [-; ], то ее ряд Фурье сходится к функции f(x) во всех точках, в которых она непрерывна. В точках разрыва функции f(x) ряд сходится к среднему арифметическому ее предельных значений слева и справа, т.е. к значению Замечание. Функция называется гладкой в интервале, если в этом интервале она непрерывна вместе со своей первой производной. Функция называется кусочно-гладкой в интервале, если данный интервал можно разбить точками разрыва 1-го рода на конечное число интервалов, в каждом из которых функция гладкая. Следствие теоремы. Теорема гарантирует разложимость всякой дифференцируемой на отрезке [–; ] функции в ее ряд Фурье не на всем этом отрезке, а лишь на открытом промежутке (–; ), однако если разлагаемая функция удовлетворяет еще дополнительному условию, что Существуют и иные достаточные признаки разложимости функций в ряд Фурье, например, следующая теорема: Теорема 4 (Дирихле). Если функция f(x) имеет на интервале (-; ) лишь конечное число максимумов и минимумов и непрерывна, за исключением, м.б., конечного числа точек разрыва 1-го рода, то f(x) разлагается в ряд Фурье, сходящийся в точках непрерывности к самой функции, а в точках ее разрыва В силу основной теоремы, если ряд является рядом Фурье функции f(x), можно написать: f(x) = Пример 1: Разложить в ряд Фурье функцию с периодом 2: f(x) = 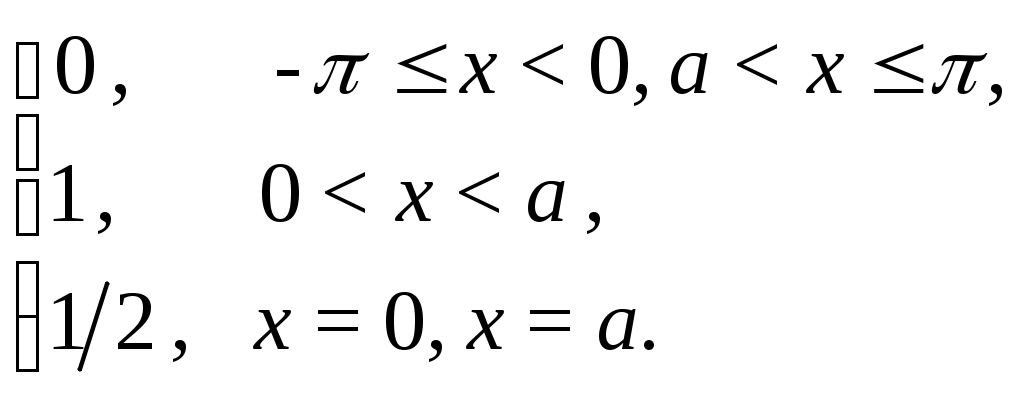 Решение: Из определения f(x) следует, что она удовлетворяет условиям теоремы о разложимости в ряд Фурье, поэтому f(x) разлагается в ряд Фурье. (См. рис. 1.) 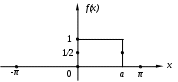 Рис. 1. По формулам (1.11)-(1.13) находим коэффициенты Фурье: а0 = 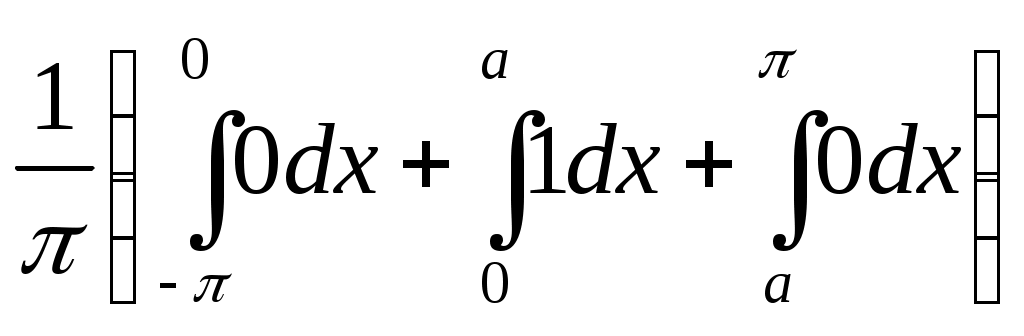 = = аn= 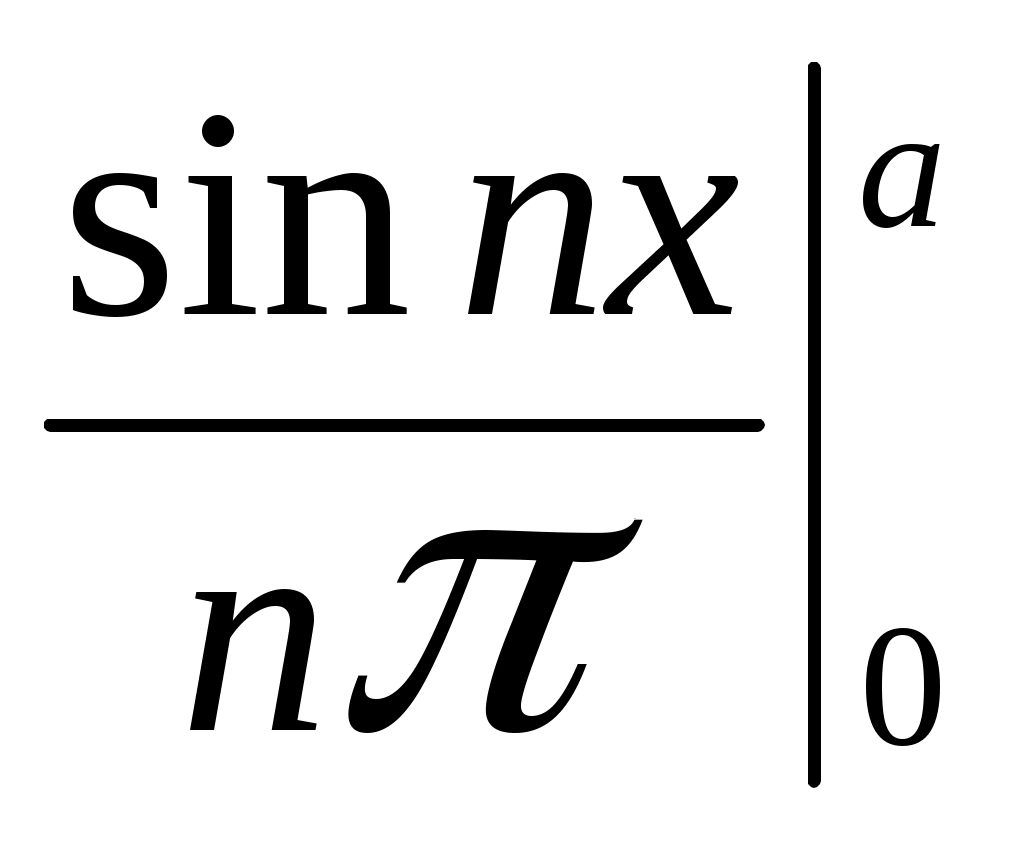 = = 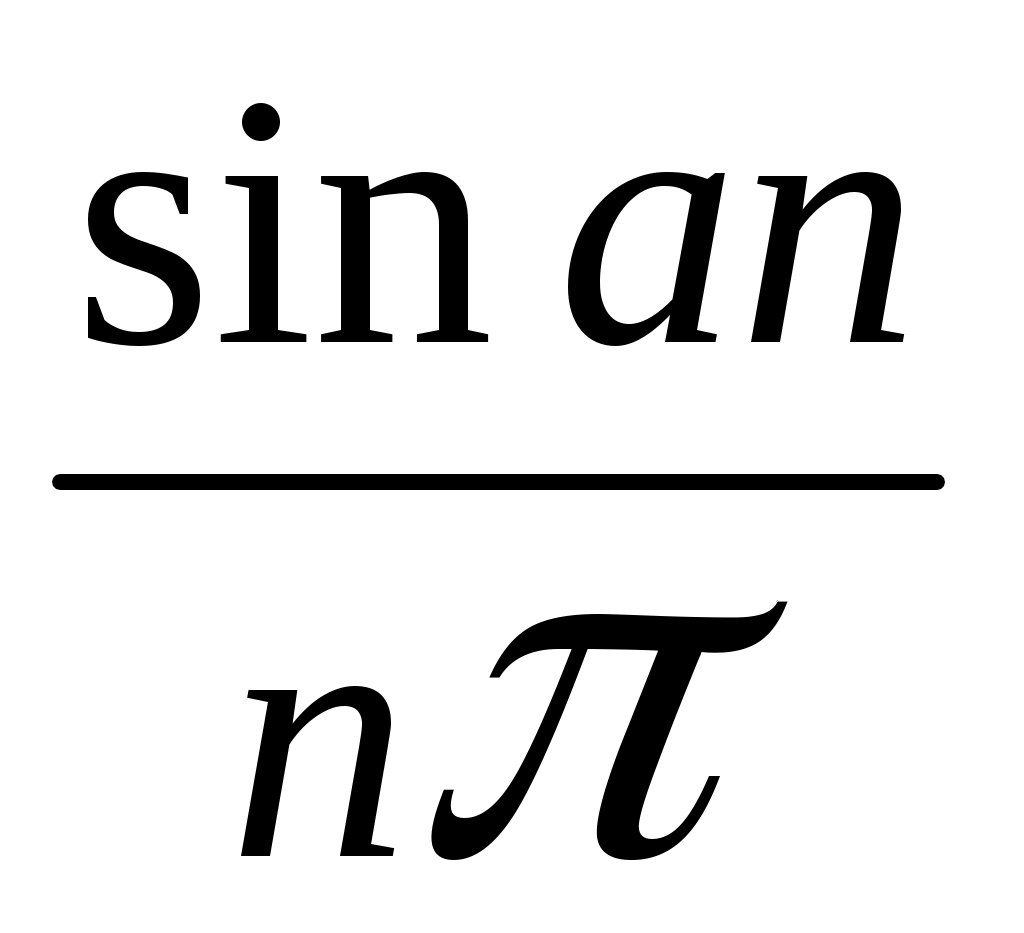 , при n 0. , при n 0.Замечание. Если n = 0, то для вычисления аn поступаем следующим образом: рассмотрим предел при n0 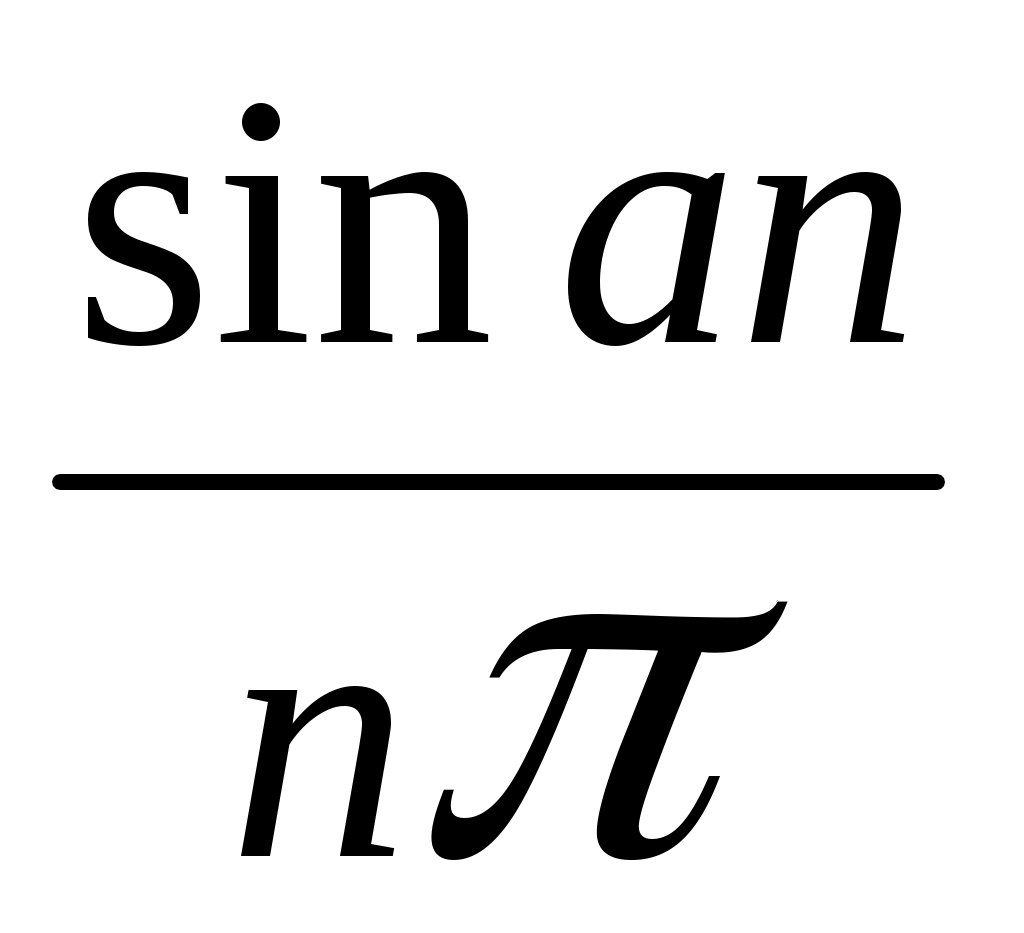 = = bn = 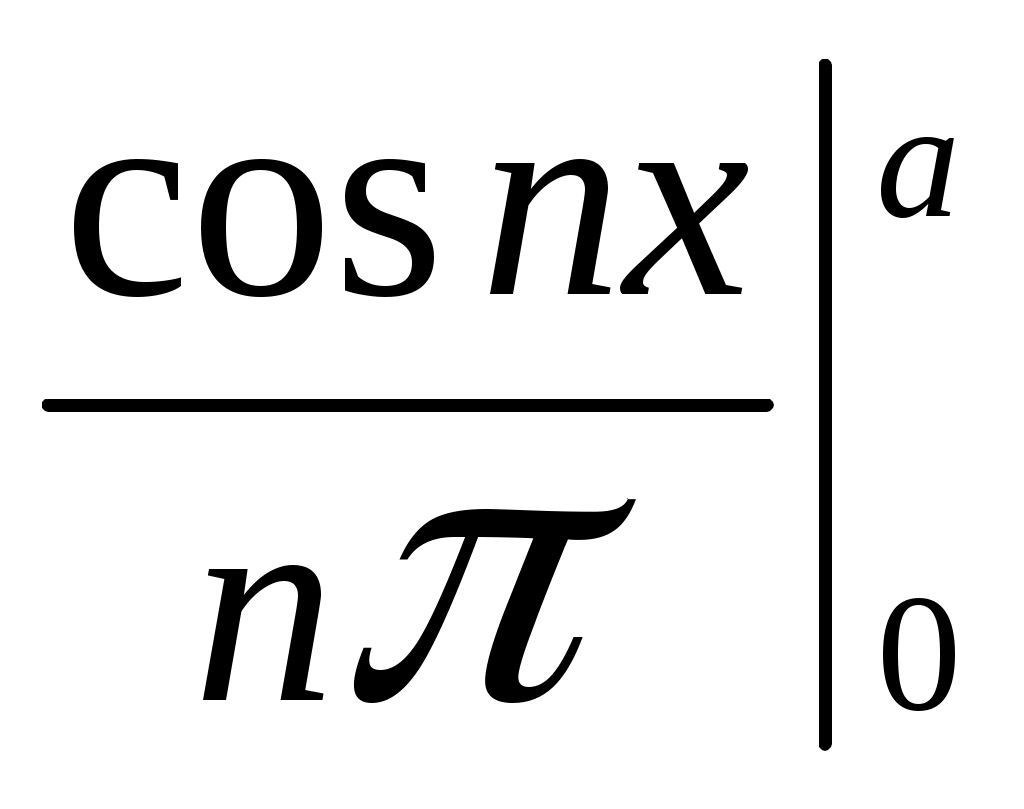 = – = –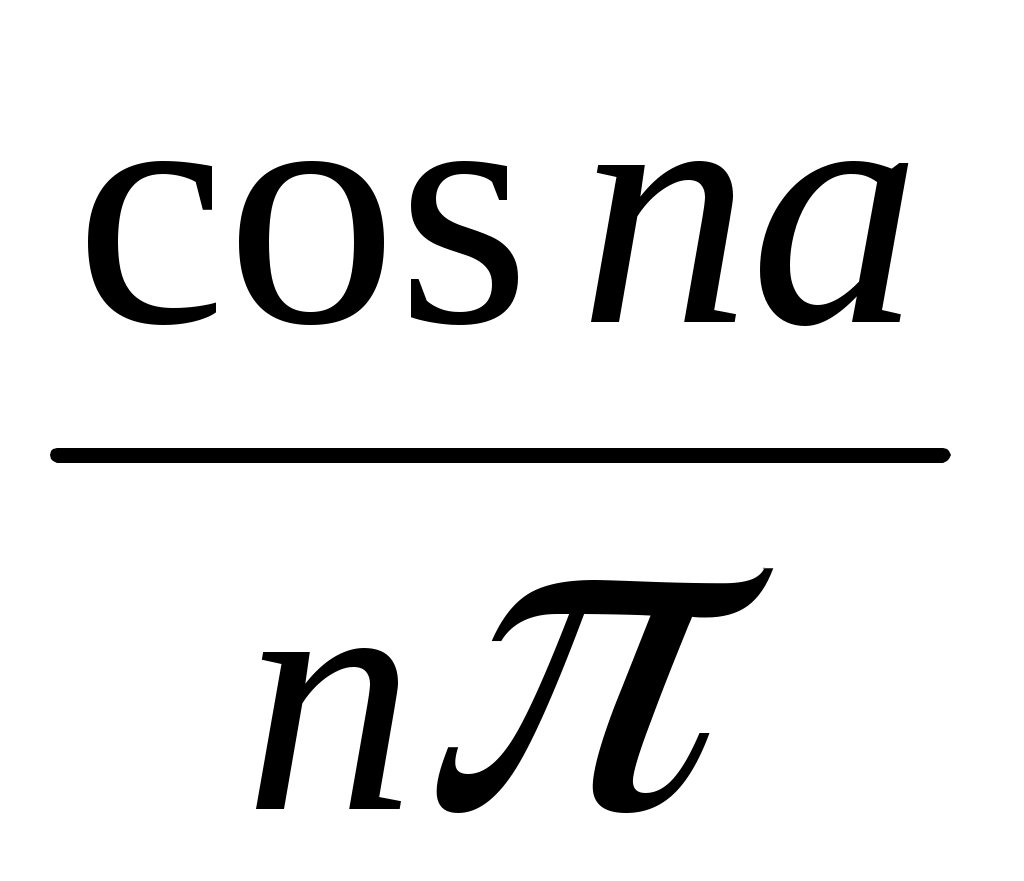 + +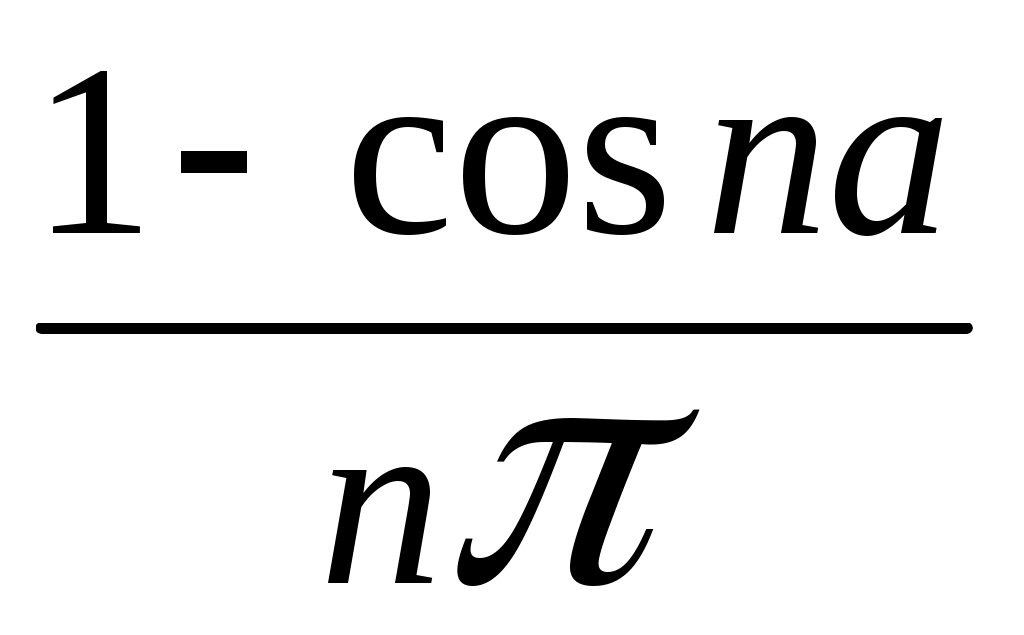 , при n 0. , при n 0.Следовательно, f(x) = В интервале [-; ] ряд сходится к функции f(x), в точках х = к 0: ( 1/2 [ f(–+0) + f(–0)] = 0 ), в точках х = a, x= 0 к 1/2 : ( 1/2 [ f(х-0) + f(х+0)] = =1/2 ). Ряд Фурье в виде простых гармоник. Спектры. Практически любую периодическую функцию можно разложить на простые гармоники с помощью тригонометрического ряда (ряда Фурье): f(x) = Запишем данный ряд в виде суммы простых гармоник, полагая коэффициенты равными an= Ansinn, bn= Ancosn . Получим: ancos n + bnsinn = Ansin( nx+ n ), где An = Тогда ряд (*) в виде простых гармоник примет вид f(x) = Ряд Фурье представляет периодическую функцию суммой хотя и бесконечного числа синусоид, но с частотами, имеющими определенное дискретное значение. Иногда n-ую гармонику записывают в виде ancos nx + bnsin nx = Ancos(nx – n) , где an= Ancosn , bn= An sinn . При этом An и n определяются по формулам (**). Тогда ряд (*) примет вид f(x) = Определение 9. Операция представления периодической функции f(x) рядом Фурье называется гармоническим анализом. Выражение (*) встречается и в другой, более употребительной форме: Коэффициенты an, bn определяются по формулам: величина C0выражает среднее значение функции за период и называется постоянной составляющей, которая вычисляется по формуле: В теории колебаний и спектрального анализа представление функции f(t) в ряд Фурье записывается в виде: т.е. периодическая функция представлена суммой слагаемых, каждое из которых есть синусоидальное колебание с амплитудой Сn и начальной фазой n, то есть ряд Фурье периодической функции состоит из отдельных гармоник с частотами, отличающимися друг от друга на постоянное число. Причем каждая гармоника имеет определенную амплитуду. Значения Сn и n должны быть надлежащим образом подобраны для того, чтобы равенство (***) выполнялось, то есть определяются по формулам (**) [Сn = Аn]. Перепишем ряд Фурье (***) в виде Определение 10. Совокупность величин Сn , то есть зависимость амплитуды от частоты, называется амплитудным спектром функции или спектром амплитуд. Определение 11. Совокупность величин n носит название спектра фаз. Когда говорят просто “спектр”, то подразумевают именно амплитудный спектр, в остальных случаях делают соответствующие оговорки. Периодическая функция имеет дискретный спектр (то есть она может быть представлена в виде отдельных гармоник). Спектр периодической функции можно изобразить графически. Выберем для этого координаты Сn и = n1. Спектр будет изображен в этой системе координат совокупностью дискретных точек, т.к. каждому значению n1 соответствует одно определенное значение Сn . График, состоящий из отдельных точек, неудобен. Поэтому принято изображать амплитуды отдельных гармоник вертикальными отрезками соответствующей длины (рис. 2). Р 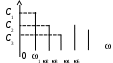  ис. 2. ис. 2.Этот дискретный спектр часто называют линейчатым. Он - гармонический спектр, т.е. состоит из равноотстоящих спектральных линий; частоты гармоник находятся в простых кратных соотношениях. Отдельные гармоники, в том числе первая, могут отсутствовать, т.е. амплитуды их могут равняться нулю, но это не нарушает гармоничности спектра. Дискретные, или линейчатые, спектры могут принадлежать как периодическим, так и непериодическим функциям. В первом случае спектр обязательно гармонический. Разложение в ряд Фурье может быть обобщено на случай непериодической функции. Для этого надо применить предельный переход при Т∞, рассматривая непериодическую функцию как предельный случай периодической при неограниченно возрастающем периоде. Вместо 1/Т введем круговую основную частоту 1= 2/Т. Эта величина – есть частотный интервал между соседними гармониками, частоты которых равны 2n/Т. Если Т ∞, то 1 d и 2n/Т , где – текущая частота, изменяющаяся непрерывно, d – ее приращение. При этом ряд Фурье перейдет в интеграл Фурье, который представляет собой разложение непериодической функции в бесконечном интервале (–∞;∞) на гармонические колебания, частоты которых непрерывно меняются от 0 до ∞: Непериодическая функция имеет непрерывный или сплошной спектры, т.е. вместо отдельных точек спектр изображается непрерывной кривой. Это получается в результате предельного перехода от ряда к интегралу Фурье: интервалы между отдельными спектральными линиями неограниченно сокращаются, линии сливаются, и вместо дискретных точек спектр изображается непрерывной последовательностью точек, т.е. непрерывной кривой. Функции a() и b() дают закон распределения амплитуд и начальных фаз в зависимости от частоты . |
